* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download project reports
Standing wave ratio wikipedia , lookup
Operational amplifier wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Schmitt trigger wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Phase-locked loop wikipedia , lookup
Radio transmitter design wikipedia , lookup
Power MOSFET wikipedia , lookup
Integrating ADC wikipedia , lookup
Voltage regulator wikipedia , lookup
Interferometric synthetic-aperture radar wikipedia , lookup
Current mirror wikipedia , lookup
Surge protector wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Power electronics wikipedia , lookup
MINI PROJECT IN TET4190 POWER ELECTRONICS FOR
RENEWABLE ENERGY
Redundance in cascaded multilevel H-bridge inverter
By:
Andreas Harstad Hallan,
Krister Haugen,
Lars Martin Hytten og
Siri Minothi
1 Summary
In this project it has been studied possibilities for including redundance in a modular power supply system
for subsea applications. The circuit studied in the project is a three-phase power supply made up by
independent inverter cells connected in series to achieve the three phase voltages. The main scope of this
project was to study how the line to line voltages can be maintained with a loss of phase voltage magnitude
in one or more phases caused by a fault in one or more cells.
A mathematical description, a Matlab® based solution tool and a PSCAD® model has been made for this
report. The MATLAB script was used to calculate the required phase voltages to restore symmetrical line
voltages after inverter cell breakdowns. The different fault situations were simulated in the PSCAD model.
The model testing shows that compensation by manipulation of the control signal gives the same line to
line voltages as in a symmetrical system. Two examples have been studied in detail along with proposed
solution for a range of other fault cases.
The lesser utilization of inverter capacity and higher cost of production are not considered in detail, but
should be a topic in further studies.
If a deeper study of the inverter is to be carried out the following subjects should also be taken into
account:
Utilization of inverters with over modulation
Optimization of phase voltages to prevent over load of one cell
Innhold
Summary ............................................................................................................................................. 2
Introduction ......................................................................................................................................... 4
Theory ................................................................................................................................................. 5
3.1
Cell components ........................................................................................................................... 5
3.1.1
Cell structure ........................................................................................................................ 5
3.1.2
Cell principle ......................................................................................................................... 5
3.1.3
Full Bridge DC-AC Inverter..................................................................................................... 6
3.2
Maximizing the output ................................................................................................................. 6
3.2.1
Pulse Width Modulation (PWM) with Bipolar Voltage Switching ........................................... 6
3.2.2
Use of third harmonics.......................................................................................................... 7
3.2.3
Cell bypass ............................................................................................................................ 7
3.2.4
Bypass equal number of cells ................................................................................................ 8
3.2.5
Neutral shift.......................................................................................................................... 8
3.3
Fault effect on output voltage ...................................................................................................... 8
3.4
Method of calculation ................................................................................................................ 10
3.4.1
Method devised by Robicon Corporation, US Patent (5986909) .......................................... 10
3.4.2
Method using Law of cosines .............................................................................................. 10
3.5
Description of the Matlab script ................................................................................................. 11
4
The case ............................................................................................................................................. 11
4.1
Pre fault case .............................................................................................................................. 11
4.2
With fault ................................................................................................................................... 12
4.3
Simple case ................................................................................................................................ 13
4.4
Complex case ............................................................................................................................. 14
4.5
Border-line case ......................................................................................................................... 15
5
Introduction to model test ................................................................................................................. 16
5.1
The PSCAD model ....................................................................................................................... 16
5.2
Test procedure ........................................................................................................................... 18
6
Normal operation............................................................................................................................... 19
7
Fault situation 1 ................................................................................................................................. 20
7.1
Fault simulation.......................................................................................................................... 20
7.2
Correcting for unsymmetrical voltages ....................................................................................... 22
8
Fault situation 2 ................................................................................................................................. 23
8.1
Fault simulation.......................................................................................................................... 23
8.2
Correcting for unsymmetrical voltages ....................................................................................... 23
9
Discussion and conclusion .................................................................................................................. 25
10
References ..................................................................................................................................... 28
1
2
3
2 Introduction
For subsea applications of power electronics there are different challenges compared to normal
surroundings. High pressure, large distance from land and the difficulty to repair any faults that may occur
causes big challenges. To maintain or replace broken components, the power supply unit must be brought
to the surface. This requires specialized vessels and also requires the production to stop. This is very
expensive, so the maintenance of the equipment must be minimized. What is demanded is a reliable power
supply that can run for 5‐7 years without interruptions due to maintenance.
Siemens’ solution to this problem is to create a modular power supply system where each of the three
phases of the power input consists of several independent cells. If one of the cells break down, it can be
bypassed automatically while the power supply keep delivering balanced three‐phase power at an
acceptable voltage level. By including redundancy in the system, it can still work properly even if some
components fail.
In the project it will be studied how the breakdown of cells affects the line voltages of the power supply in a
PSCAD model of the circuit. It will also be studied how to calculate adjustments required for restoring the
system to normal operation from the various fault situations. These solutions will be tested through
simulations in the PSCAD model.
3 Theory
3.1 Cell components
3.1.1 Cell structure
Figure 1: Simplified diagram of a 15 cell converter
The main motivation for this circuit design is to achive redundance in a three-phase power supply for a
motor used subsea. The subsea application requires a power supply that can tolerate faults in some of the
components without a drop in the output voltage. The circuit is made up of independent cells working as
individually controllable AC sources connected in series. If a fault occurs in one of the cells it may be
bypassed within a half second. The other cells may then be adjusted to restore the original line voltages.
The number of cells in each phase will depend on the desired output voltage and the need for redundance.
The phase voltages become the vector sum of the cell voltages of each phase. Figure 1 from [2] shows a
modular three-phase power supply and five cells in each branch.
3.1.2 Cell principle
Figure 2 shows an inverter of the type used in the power supply. In this application a rectified voltage from
a three-phase transformer is used as the DC source, creating a galvanic separated cell. Because each cell is
only exposed for the voltage level given from the DC source, low voltage components may be used to
achieve the high output voltage required for the motor. Low voltage component is an advantage
considering price and number of components on the market.
Figure 2: Typical cell with bypass contactor
3.1.3 Full Bridge DC-AC Inverter
Figure 3: Single-phase full-bridge inverter
Figure 3 shows a basic full bridge inverter, as described in [1].
The full bridge inverter is used to ensure that enough power can be delivered.
Because of the voltage limits of electrolyte capacitors and especially since this inverter will be used for high
voltage applications, it is necessary to use at least two capacitors in series as the capacitor bank.
3.2 Maximizing the output
3.2.1 Pulse Width Modulation (PWM) with Bipolar Voltage Switching
To achieve a sinusoidal output voltage waveform with the desired frequency, a triangular waveform is
compared with a sinusoidal control signal. The comparison of the two signals sets the pulse width that
controls the swiching intervals of the inverter.
Figure 4: PWM with bipolar voltage switching
In Figure 4 from [1] it is shown how PWM can be used to create a sine wave by changing the pulse width,
the pulse shown in figure 8-12 (b) is the output voltage.
3.2.2
Use of third harmonics
By the use of 3rd harmonic modulation it's possible to widen the sinusoidal output voltage, and the
therefore getting more voltage time from the inverter by increasing the RMS value of the voltage. This
gives more voltage with the same current, giving more power delivered. The 3rd harmonic will be cancelled
in the line voltage, which is transferred to the motor, thus it doesn't create any problem for the load. It still
sees a perfect sinusoidal wave. Using this technique is an object for further studies of the cell converter.
3.2.3 Cell bypass
An important part of achieving a high reliability is by the use of cell bypass. Because of the galvanic
separation between the supply voltage and the cell it's possible to disconnect any cell in less than a
second. In figure 4-1 the connection of the bypass contactor is shown. In case of a fault in a cell the bypass
contactor will short the output terminals of the cell, regardless of which component that fails, allowing the
whole system to continue operating at a lower voltage for that string of cells.
3.2.4
Bypass equal number of cells
If one or more cells break down the line voltage will not be the same for all three lines. One way to solve
this problem is to take away more cells so that we end up with the same number of cells in all of the
branches. The shape of the triangle in figure 4-2 will then be restored.
3.2.5 Neutral shift
Another and better way is to exploit the fact that we can move the neutral point. This will have an affect on
the phase voltages and the phase angels, but that is not a problem since the motor only cares about the
line voltages.
3.3 Fault effect on output voltage
In the ideal case we have three phases with the same amplitude shifted 120 degrees as Figure 5
illustrates.
Figure 5 - Phase and line voltages, represented as phasors, in optimal case
The phase voltages are:
With:
Hence the line to line voltages are:
We see that the amplitudes are the same for all line to line voltages with a 120 degree shift. These
vectors rotate and keep the same amplitude and shift to produce a sinusoidal shaped voltage on
the output of the inverter.
In a case where the voltage on one of the phases drop because of a fault in one of the inverter
cells the picture will change drastically. As an example the voltage on phase R is reduced by 40 %
(for example if 2 of 5 inverters are short circuited). The phase shift is the same, but with
amplitudes:
This is illustrated in Figure 6 where the original line to line voltages are dotted lines.
Figure 6 - Phase and line voltages, represented as phasors, after fault
The shows a change in both amplitude and phase angle in the line voltages connected to phase R.
The same calculations as for Figure 5 give:
As the voltage UST is still unchanged this gives a dramatic asymmetry in the line voltages which will
affect the unit connected to the bus, probably in an unfavorable manner.
3.4 Method of calculation
There are many ways of looking at this problem. In this report two different approaches are studied and a
detailed description is given to one of them.
3.4.1 Method devised by Robicon Corporation, US Patent (5986909)
This method is from the patent of Peter W. Hammond and Marc F. Aiello at Robicon Corporation, patented
in 1999, the company was bought by Siemens in 2005. The patent covers the unit described in this report,
and also provides a selection of the table from the report, showing how much output voltage is lost given
the loss of a specific number off cells. The complete table is shown in Appendix I.
3.4.2 Method using Law of cosines
Since there already was a complete solution for comparing the output voltage to the maximum voltage as
you loose cells in each phase. We decided to base our calculations on the principle that the line to line
voltage had to be kept constant, and then try to calculate how the other phases would have to compensate
and phase angels adjusted to keep the required line voltage.
Using the Law of cosines we can easily calculate a missing angle or length of a line in a triangle. To
move from one triangle to the next an extra variable β was used to describe the angle as shown in
Figure 7. For this method to work we assume that two of the phase voltages can be set by us, and
that the line voltages are constant. We build this method around Vc usually being the weakest, Va
adjustable but mainly the same as before fault, and then Vb and the phase angels are calculated to
complete the triangle.
By manually increasing Va it's possible to reduce the pressure on Vb and keep the phase angels closer to
normal. Or the ability to adjust Va could be used to simulate a fault in that phase as well. In this case the
script calculates what Vb must be to keep the line to line.
Using this method it is possible to create some worst case scenarios that the inverters must be able to
handle, and based on that calculate how much voltage you would need to begin with. This provides a more
direct approach to the redundancy problem, and how much of it we need, that the method in section 1.1.
Figure 7: The three-phase triangle with angles
3.5 Description of the Matlab script
The script requires Va, Vc and a line voltage ex. Vab as input. Based on this it returns the phase
angels and magnitudes of each phase.
It uses the Law of cosine to calculate alpha on line 15, based on the assumption that Va and Vc is known. If
one or both of the line voltages is large enough the angle returned to alpha(3) will be a complex number;
an unphysical solution. The voltage on phase A is then increased in small steps until the two vectors are
long enough to support Vac. Then, using the line voltage Vac, Vc and Va the angle beta(1) is calculated, and
given that the line voltages are balanced we get beta(1)+beta(2)=60°. Using beta(2), Vbc and Vc we can
then calculate Vb, subsequently we have all three phases and line voltages. The script finishes by
calculating the phase angels alpha(2) and placing alpha(1) as the reference.
At the final lines, from 36 and down, some output is generated, mostly to instantly show the result, and
that the phase angels add up to 360°.
4 The case
This section provides a theoretical description of the three phase star coupled system used to create the
line voltages, and gives examples of how the disconnection of the neutral point from the rest of the system
can be used to compensate for the loss of voltage from one or more phases without reducing line to line
voltage or alter the phase angels on the line voltage.
4.1 Pre fault case
In a balanced three phase system the phase voltages and line voltages can be organised as shown in Figure
8.
Figure 8: Three-phase triangle in the pre-fault state
In this case the phase voltages A, B and C are all equal, same for α1, α2 and α3 all equal to 120°. This is the
normal case for a 3 phase system.
4.2 With fault
Figure 9 shows a situation where phase C is reduced to only 80% voltage compered to the normal case in
section 2.1. This reduces the line voltage on Vac and Vbc, it also interferes with the all the phase angels,
leaving the line voltages in a poor state.
Figure 9: Three-phase triangle after fault
To compensate for this it is possible to move the neutral point N, this case is shown in section 1.3.
4.3 Simple case
In this simple case only one of the phase voltages are limited. Vc can only reach 80% capasity, but by
increasing Vb by 26% and keeping Va the same, we change the phase angels to α1=99.36° α2=112.43° and
α3=148.21°, the resulting line voltage is then kept as before with an angle of 120° between the phases. This
case is shown in Figure 10.
Figure 10: Three-phase triangle with phase voltage Vc limited to 80%
4.4 Complex case
In a more complex example we have a case where the voltage on phase C is limited to only 20%. Again it is
possible to compensate for this by increasing the other phase voltages and shifting the neutral point. The
result is shown in Figure 11.
Figure 11: Three-phase triangle with phase voltage Vc limited to 20%
As seen in Figure 11 Va is 53% larger, Vb is 62% larger and Vc at only 20%. To balance this system it's
necessary to change the phase angels to α1=66.60° α2=121.86° and α3=171.54°.
4.5 Border-line case
As an extreme case the lowest sum of voltages from Va and Vb that can still maintain the required output
voltage is when the sum of to phases only are enough to support one of the line voltages. This case is
shown in figure 5. It this case both Va and Vc is reduced by 13.4%.1 To keep the line voltages Vb have to be
increased by 62%, and the phase angles shifted to α1=90° α2=90° and α3=360°.
Altough this is may not be a very realistic case, requirering the phases to opperate at only 62% during
normal opperation, it still shows it possible to handle a 13.4% loss in two phases without loosing line
voltage. As 13.4% is related to normal state, and given an equal redundancy in all three pahses of 62%, the
total voltage reduction is actually 46,5%, almost half the potential voltage. An illustration of the border
case is given in Figure 12.
Figure 12: Three-phase triangle with phase voltage sum of Vc and Va at minimum
In the above figure it can be seen how vulnerable the line voltages become in such an extreme
case.
3
1 2 100%
1
13.4% is derived from
, Where
the two phases.
3 is the ratio between line and phase voltages, divided between
5 Introduction to model test
The mathematical description developed earlier suggests phase voltages to maintain line to line voltages in
case of a fault. This description will now be tested in a model created with the simulation tool PSCAD®. The
scope of the tests is to show that a multi cell inverter system improves reliability in control applications.
There will be presented five cases. The first is the no-fault case where the conditions are as in normal
operation. The next two are different fault conditions with solutions as the two last. The solutions will be
obtained with the Matlab script.
5.1 The PSCAD model
The model consists of two parts. The first is a full-bridge inverter with bipolar switching, and the second is
the generation and comparing of the control signal. In this case the control signal is sinusoidal since we
would like to illustrate the conditions which the controller usually would operate in example connected in
front of an AC motor. The input is a DC-source to idealize a rectified grid voltage. The voltage of the DC
source was set to 12.7 kV to give a line to line voltage of 6.6 kV, as desired in the case studied.
Three inverters are Y-connected with the possibility of changing the DC-input to simulate loss of cells in
Siemens’ multi cell system. Then the control signal can be regulated to maintain the angle and magnitude
of the line to line voltages. Figure 13 shows the layout of the inverters used for simulations as it is drawn in
PSCAD®.
Figure 13: Y-connected switchmode inverters
To control the transistors a circuit is constructed with a one generator giving a sinusoidal wave at the
output, and one with a triangle shaped signal. These signals are compared in a comparator which returns
the value 1 if A>B, and 0 if A<B in Figur 14. To ensure bipolar switching a logic inverter is placed between
signal T1 and T2 in Figur 14. This gives opposite signal on the two pairs of each cell in Figure 13. The
triangular wave signal frequency is what gives the switching frequency of the transistors, whilst the phase
angle, magnitude and frequency of the sine wave give the output voltage characteristics. The control circuit
as it is drawn in PSCAD® is presented in Figure 13.
Figur 14: Control circuit for one cell in the switch mode inverter
We can use this layout and still assume that this is a multi cell construction since a series connection of cells
with a control signal having the same phase angle will effectively result in just adding of voltage
magnitudes. The amplitude modulation, ma, is set to a low value to give possibility of regulation in the
linear range. This will lead to low amplitude of the first harmonic and therefore inefficient use of the
inverter. Control signal with ma > 1 can be used to give a higher voltage-time area, and improved efficiency.
To illustrate the improved redundancy of the multi cell system over modulation is not necessary, but should
be considered in detail if a practical inverter are to be built. Note that the switching frequency is set to be
very low in to improve readability of plots. The frequency modulation, m f, is the same for all experiments.
5.2 Test procedure
The same procedure was followed for all cases, and consists of the following:
1. Lower DC input
To simulate that one or more of the cells in a phase is short circuited.
2. Calculate phase voltages with Matlab script
The desired line voltages are known as the pre fault voltages. The new conditions are inserted into the
model, and a solution is obtained.
3. Insert theoretical values
The control signal phase and amplitude modulation is changed according to the theoretical values. New
phase voltage magnitudes are obtained with the following formula in the linear range:
manew maold *
Vphaserequired
Vphasew / fault
4. Register new phase voltages and the resulting line to line voltage.
6 Normal operation
The aim for the first experiment was to study the normal steady state operation of the circuit. The three
DC-voltage sources were set to the initial voltage 12.70 kV, representing the branches with all six cells
intact. The line voltages from the simulations and their fundamental components are plotted in the figures
below.
Figure 15: Eab with fundamental components, normal operation
Figure 16: Ebc with fundamental components, normal operation
Figure 17: Eca with fundamental components, normal operation
Figur 18: Fundamental components of Eab, Ebc and Eca, normal operation
As seen from figure 18 the fundamental components of the three voltages are symmetrical with a phase
shift of 120°. The fundamental components of the three phase voltages have a RMS value of 6.60 kV in
normal operation.
7 Fault situation 1
7.1 Fault simulation
This experiment simulates the loss of one of the six cells in one of the phases. To illustrate this effect, the
DC-voltage of the source in phase C was set to 10.583 kV, which corresponds to a loss of one sixth of the
initial voltage. Phase A and phase B remained at the initial value.
Figure 19: Eab with fundamental component, fault situation 1
Figure 20: Ebc with fundamental component, fault situation 1
Figure 21: Eca with fundamental component, fault situation 1
Figure 22: Fundamental components of Eab, Ebc and Eca with cursors, fault situation 1
As seen from figure 19, the line voltage Eab remains at the pre-fault value after the loss of one cell in phase
C. Ebc and Eca both get the same lower value as showed in figure 20 and figure 21. The horizontal cursors
in figure 22 are included to illustrate the lower amplitude of Ebc and Eca. The numerical RMS values of the
fundamental components are included in Table 1.
7.2 Correcting for unsymmetrical voltages
A MATLAB script (appendix 2) was written to obtain the new phase voltages required for restoring
symmetrical line voltages. The new ma values for the control circuit were calculated based on these
voltages. A new simulation was conducted with the new ma values. The resulting line voltages equal the
initial line voltages with only small deviations due to round-off errors. The calculated phase voltages and
the resulting values for ma are included in Table 1.
8 Fault situation 2
8.1 Fault simulation
This experiment simulates the loss of two of the six cells in phase C and one of six cells in phase A. To
illustrate this effect, the DC-voltage of the source in phase C was set to 8.467 kV, which corresponds to a
loss of one third of the initial voltage. The DC-voltage of the source in phase A was set to 10.583 kV, which
corresponds to a loss of one sixth of the initial voltage.
Figure 23: Fundamental components of Eab, Ebc and Eca with cursors, fault situation 2
As seen from figure 23 all three of the line to line voltages get a lower value after the fault. The horizontal
cursors are included to illustrate the different amplitudes.
The numerical RMS values of the fundamental components are included in Table 1.
8.2 Correcting for unsymmetrical voltages
Again the MATLAB script was used to obtain the new phase voltages required for restoring symmetrical line
voltages. New ma values for the control circuit were calculated based on these voltages, and a new
simulation was conducted with the new ma values. The resulting line voltages were equal the initial line
voltages except from some small round-off errors. The calculated phase voltages and the resulting values
for ma are included in Table 2.
To show that the system can maintain symmetrical line voltages for a broad number of scenarios, two
additional fault situations were simulated. The results are included in Table 2 without further discussion.
Table 1 Post faul line voltages before compensation
Post fault line voltages before compensation
Case
Eab
Ebc
Eca
0
Normal operation
6.594 kV
6.594 kV
6.594 kV
1
Loss of 1 of 6 cells in
phase C
6.594 kV
6.052 kV
6.053 kV
6.053 kV
5.531 kV
4.956 kV
2
Loss of two of six cells
in phase C and one of
six in phase A
Table 2 Phase voltages to restore symmetrical line to line voltages
Post fault condition after compensation
Case
Phase A
Va
Phase B
ma
Vb
Phase C
ma
Vc
ma
1
Loss of 1 of 6 cells in phase
C
3.81 / 0° kV 0,600
4.59 / 256.8° kV
0,722
3.18 / 141.6° kV
0,600
4.07 / 0° kV 0,769
5.57 / 275.1° kV
0,877
2.54 / 172.6° kV
0,600
2
Loss of two of six cells in
phase C and one of six in
phase A
Above: Discussed in detail. Below: Additional examples
3
Loss of one cell in phases A
and C
3.44 / 0° kV
-
5.50 / 267.8° kV
-
3.18 / 172.5° kV
-
3.32 / 0° kV
-
5.32 / 263.1° kV
-
3.32 / 166.2° kV
-
4
Loss of two cells in phase A
and C and loss of one cell in
B phase
9 Discussion and conclusion
The tables on the previous page show that loosing cells in one or more of the phases leads to a different
line voltages. In most cases the line voltages will be unsymmetrical.
Table 1 shows the resulting post fault line voltages for fault situations 1 and 2 if no compensation is
applied. Loosing a cell in phase C makes both line voltages Ebc and Eca decrease by 8 % while Eab however
remains at the initial voltage. Loosing two of six cells in phase C and one of six in phase A makes Eab
decrease by 8 %, Ebc by 16% and Eca by 25%.
Table 2 shows how the line voltages may be restored to the initial operation mode from fault situation 1
and 2 in addition to two other fault scenarios. The compensation is done by adjusting the value of ma and
the phase angle between the voltages.
The adjustments may be accomplished in many different ways. There are many combinations of ma values
and phase angles that yields the symmetrical initial voltages from a given fault situation. The combinations
in the table are chosen somewhat arbitrarily. The choice of values may be optimized to some criterion, by
for instance minimizing the highest voltage delivered from a single cell. This is beyond the scope of this
project.
The degree of redundancy of the system depends on the initial value of ma. By setting ma to a low initial
value, the voltage of each cell may be increased much while still being in the linear region of the control
circuit. A low initial value of ma will however lead to low utilization of the equipment. The trade-off
between redundancy and utilization must be balanced for the particular case.
The results from the simulations and the theoretical values calculated with the MATLAB script are
practically equal. The component parameter values used in the PSCAD model were set to the default values
which are almost ideal. The parameter values of the components used in the Siemens circuit were not
known when this report was written. However, electrical components for this kind of applications usually
have an efficiency factor close to unity. It can be assumed that the simulation results will also be applicable
to the actual circuit.
In more detailed studies of this subject there are a lot of other considerations that has to be taken into
account. The line length and on shore grid connection also have great impact on system redundancy. Better
utilization with over modulation an optimization of phase voltages to ensure the lowest possible voltage
over each cell is also subjects that would be interesting in further developments.
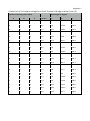
Appendix 1
A selection of line output voltage for a 6 cell 3-phase H-bridge inverter from [3]
Number of working cells in pahse
A
B
Phase angels in degrees
C
% of Vmax
α1
α2
α2
6
6
6
100
0.0
120.0
240.0
6
6
5
94.1
5.4
114.6
240.0
6
6
4
87.8
10.5
109.5
240.0
6
6
3
80-9
15.5
104.5
240.0
6
6
2
73.6
20.4
996
240.0
6
6
1
65.9
25.2
94.8
240.0
6
6
0
57.7
30.0
90.0
272.3
6
5
5
88.5
0.0
113.1
246.9
6
5
4
82.1
5.0
106.5
249.3
6
5
3
75.1
9.8
99.8
253.6
6
5
2
67.2
14.5
92.7
263.2
6
5
1
55.1
20.5
82.4
311.3
6
4
4
75.5
0.0
101.4
258.6
6
4
3
67.3
4.8
91.2
268.4
6
3
3
50.0
0.0
60
300.0
5
5
5
83.3
0.0
120.0
240.0
5
5
4
77.4
6.4
113.6
240.0
5
5
3
70.9
12.5
107.5
240.0
5
5
2
63.8
18.5
101.5
240.0
5
5
1
56.2
24.3
95.7
240.0
Appendix 2
%[V,alpha]=vbEstimate(Va,Vc,Vab);
%Calculates Vb in an unbalanced 3 phase system, with the LL voltages
%constant and symetrical with Va beeing as small as possible
% V(1)=Va
% V(2)=Vb
% V(3)=Vc
%
%Eks.:
%[V,alpha]=vbEstimate(1,0.8,sqrt(3));
function [V,alpha]=vbEstimate(Va,Vc,Vab)
Vbc=Vab;
Vac=Vab;
alpha(3)=acosd((Va^2+Vc^2-Vac^2)/(2*Va*Vc));
%Increase phase voltages in phase a and c if they are to low
while(~isreal(alpha(3)))
Va=Va+Va*0.01;
%Vc=Vc+Vc*0.01;
alpha(3)=acosd((Va^2+Vc^2-Vac^2)/(2*Va*Vc));
end
beta(1)=acosd((Vac^2+Vc^2-Va^2)/(2*Vac*Vc));
beta(2)=60-beta(1);
Vb=sqrt(Vc^2+Vbc^2-2*Vc*Vbc*cosd(beta(2)));
alpha(1) = 0; % Set reference voltage angle
alpha(2)=alpha(3) + acosd((Vb^2+Vc^2-Vbc^2)/(2*Vb*Vc));
V(1)=Va;
V(2)=Vb;
V(3)=Vc;
disp(' ');
disp(['Sum of alpha angels = ' , num2str((acosd((Va^2+Vb^2-Vab^2)/(2*Va*Vb))+acosd((Vb^2+Vc^2Vbc^2)/(2*Vb*Vc))+acosd((Va^2+Vc^2- … … Vac^2)/(2*Va*Vc)))) , ' degrees']);
if(round(acosd((Va^2+Vb^2-Vab^2)/(2*Va*Vb))+acosd((Vb^2+Vc^2 …
… Vbc^2)/(2*Vb*Vc))+acosd((Va^2+Vc^2-Vac^2)/(2*Va*Vc)))==360)
disp('Hurray!');
end
disp(' ');
disp(['Va= ', num2str(V(1)) , ' Vb= ', num2str(V(2)) , ' Vc= ', …
… num2str(V(3))]);
disp(['alpha1= ', num2str(alpha(1)) , ' alpha2= ', num2str(alpha(2)) , '…
disp(' ');
end
… alpha3 ', num2str(alpha(3))]);
10 References
[1] Mohan, Undeland, Robbins. Power Electronics, Wiley & Sons
[2] ROBICON Perfect Harmony Engineering Manual, Siemens AG 2009
[3] US Patent (5986909), Peter W. Hammond, Marc F. Aiello, Robicon Corporation, 1999.
[4] - http://www.motorlab.com/Motor%20Lab%20Web%20Site_files/05%20-%20PSCAD.htm – Example
used as basis for PSCAD Script