Download Discrete devices: FETs - UBC Engineering Physics Project Lab

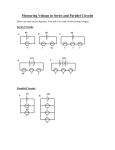
Discrete devices: FETs
Field Effect Transistors
Gate voltage either
ENHANCES or
DEPLETES the
conduction channel.
JFET = Junction FET
MOSFET = Metal Oxide
Semiconductor FET
MOSFETS have an
insulating layer at gate
so draw less current.
Current passing from source to drain now controlled by
VOLTAGE at the gate
(rather than by CURRENT into the base as in a BJT).
1
12V
+V
12V
+V
R8
10k
Discrete devices: FETs
R1
10k
Q3Effect Transistors
Q4
Field
MTP2955
MTP2955
R2
R7
There are FOUR
100
100 kinds of MOSFETs:
Q8
2N3904
HB-2
Enhancement Mode:
Q5
2N3904
N type
HB-1
P type
M1
12V
+V
12V
+V
12V
+V
Q7
2N3906
Q6
2N3906
Id
R6
100
R8
10k
Q1
Q2
HUF
75321MTP3055
MTP3055
+
R5
10k
12V
+V
Vgs -
-
Vgs +
Q3
R3
Q4
MTP2955
MTP2955
100IRF5305
R7
100
Q8
2N3904
HB-2
R4
10k
Id
Q5
2N39
M1
12V
+V
Increasing Vgs increases Id.
Q7
2N3906
R6
100
Depletion : Increasing Vgs decreases Id
2
2
Q1
Q2
3
Discrete devices: FETs
Enhancement: N type
12V
+V
P type
12V
+V
12V
+V
12V
+V
R7
100
L1
R8
10k
Q3
S1
IRF5305
MTP2955
HUF 75321
MTP3055V
R7
100
R8
10k
L1
S1
4
Discrete devices: FETs
12V
+V
5V
12V
+V
R7
100
L1
S1
HUF 75321
MTP3055V
R8
10k
gds
GND
5
Discrete devices: FETs
12V
+V
5V
12V
+V
R7
100
L1
S1
HUF 75321
MTP3055V
R8
10k
GND
6
Discrete devices: FETs
If after closing S1 (and turning on the LED)
we cut the circuit at the red line:
12V
+V
1. The LED will stay lit
2. The LED will go off
12V
+V
R7
100
L1
S1
HUF 75321
MTP3055V
R8
10k
7
Discrete devices: FETs
12V
+V
5V
12V
+V
R7
100
L1
S1
MTP3055V
R8
10k
GND
Gate is floating, but lamp is still lit!!
8
Lecture 2 – Analog circuits
Seeing the light…..
I
t
IR detection
Noise sources:
• Electrical (60Hz, 120Hz, 180Hz….)
• Other electrical
• IR from lights
• IR from cameras (autofocus)
• Visible light
V1
9V
+V
IR light
Q1
OP805
RL
Vout
Vout
~ mV
t
What we want: 0 – 5 V DC signal representing the IR amplitude.
Analog circuits – filtering and
detection
IR
DC
detect
block
Amplify
Peak
detect
Filter
Analog circuits – filtering and
detection
IR
DC
detect
block
Amplify
Peak
detect
Filter
Analog circuits – discrete devices: BJT
Application: light detection
Phototransistor:
Acts like BJT except charge carriers
generated by incident light add to the base
current.
In other words, Ic Incident light
V1
9V
+V
Ic
+
Q1
OP805
RL
Vout
For the circuit below,
1) Smaller R increases the DC sensitivity to light
2) Larger R increases the DC sensitivity to light
+
Selecting RL ….
Vout = Ic * RL
Analog circuits – filtering and
detection
Z2/Z1= 3
What is the result of the following:
Vout
+
Z1
Z2
Vout =
1)
3)
2)
4)
Analog circuits – filtering and
detection
IR
DC
detect
block
Amplify
Peak
detect
Filter
Analog circuits – DC block
Capacitors:
• Open circuits for DC
• Short circuit at high frequencies
Analog circuits – filtering and
detection
IR
DC
detect
block
Amplify
Peak
detect
Filter
Analog circuits: Op-amps
+Vcc
V+
+
Ideal op-amp:
V-
Vout
-
K ~ 106 (at DC!)
-Vcc
With feedback to
limit gain:
Vout = K (V+ - V-)
V+
+
V-
-
Vout
V- = Vout
Vout = K (V+ - Vout)
When negative feedback is
applied to an op-amp, V+ = V-
….if the amplifier is within its
operating range.
Vout(1+K) = KV+
Vout=V+(K/(1+K))
Vout= V+
The next few slides will show some bad design choices
Analog circuits: Op-amps
Eg: Inverting
amplifier.
Vin
+
V-
Z1
-
V- = 0
I1 = Vin/Z1
Z2
I1
Vout
Vout = 0 – Z2I1
Vout= - (Z2/Z1) Vin
Eg 1: Z2 = 100kW
Z1 = 10kW
Vout= - 10 Vin
Eg 2: Z2 = 100kW
Z1 = 1 W
Vout= - 100,000 Vin !!
Not likely….
10x gain is a
“reasonable” value
Analog circuits: Real Op-amps
+
Vin
Z1
I1
V-
Vout
Z2
Eg 2: Z2 = 100kW
Z1 = 1 W
Vout= - 100,000 Vin !!
Several problems:
• I1 = 1A for Vin = 1 V !! (excessive load for upstream circuitry)
• Gain Bandwidth product ~ 3 MHz. This would limit the
bandwidth of the amplifier from DC up to 30 Hz (i.e. not a very
responsive system!).
Analog circuits: Real Op-amps
Things to consider:
• Input impedance
• Gain Bandwidth product
• Bias Currents
+
• Voltage limitations
Vin
• Output current limitations
Z1
I1
V-
Z2
Since V- is a virtual ground, input
impedance seen by Vin is Z1
Vout
Analog circuits: Real Op-amps
Things to consider:
• Input impedance
• Gain Bandwidth product
• Bias Currents
• Voltage limitations
Vin
+
V-
Vout
-
• Output current limitations
Since Op-amp inputs source or sink very little
current (depends on type) , input impedance in this
case is very high. This is a commonly used buffer to
separate your low impedance circuit from a sensitive
source that you need to measure without drawing
current.
Analog circuits: Real Op-amps
+
Things to consider:
Vin
• Input impedance
• Voltage limitations
Open loop gain (K)
log K
• Output current limitations
Slew-rate is a similar
limit: it is a limit on
the rate of change of
output voltage
-
Z2
I1
• Gain Bandwidth product
• Bias Currents
V-
Z1
Vout
20
Frequency
100
kHz
log w
Gain-Bandwidth limit (Hz) = Gain * Max. Frequency = CONSTANT
TL082: Gain*Bandwidth = 3 MHz
 This means that at a gain of 100, Bandwidth is 30 kHz.
Analog circuits: Real Op-amps
Things to consider:
• Input impedance
• Gain Bandwidth product
• Bias Currents
• Voltage limitations
+
Vin
Z1
V-
Vout
Z
I1
2
• Output current limitations
Op-amp terminals can act as small current
sources. These Bias Currents can become
large error or offset voltages if the resistors
in the circuit are large.
Eg: 20 nA bias current * 10 MW = 200 mV!
Analog circuits: Real Op-amps
+Vcc
Things to consider:
• Input impedance
• Gain Bandwidth product
V+
+
V-
Vout
-Vcc
• Bias Currents
• Voltage limitations
• Output current limitations
Op-amp input voltages (V+, V-) must be at least a few
volts away from the power rails (+Vcc, -Vcc).
Applying input voltages equal or near the power rails
will cause the Op-amp to behave unexpectedly.
Rail-to-rail Op-amps are an expensive solution to this
limitation.
Analog circuits: Real Op-amps
+Vcc
V+
Things to consider:
• Input impedance
+
V-
• Gain Bandwidth product
Vout
-Vcc
• Bias Currents
• Voltage limitations
• Output current / voltage limitations
Op-amp output terminals can only provide a few mA
of current. Motors, lamps and similar high current
devices cannot typically be driven by a normal OPamp. High power Op-amps exist that can provide
much higher current levels. Output voltage range is
also limited within a few volts of the power rails.
Q: We wish to amplify a 100 kHz, 10mV p-p sine wave, as much as
possible. Which is the best circuit?
100k
V2
-5m/5mV
1)
100k
9V
2k
9V
+
2k
+
Vout
100kHz
TL082
120k
V2
-5m/5mV
2)
120k
9V
10k
10k
100kHz
10k
120k
10k
TL082
-9V
TL082
120k
9V
+
Vout
-9V
-9V
9V
10k
+
TL082
120k
3)
9V
+
TL082
-9V
V2
-5m/5mV
100k
9V
+
100kHz
TL082
9V
+
10k
TL082
-9V
+
Vout
TL082
-9V
Analog circuits: Real Op-amps
Application: amplifier stages
R3
30k
U1
TL082
Vin
Vout
1k
R2
R6
1k
10k
R1
Total gain: 30*30*11 = 9900
Input impedance = high
Max Bandwidth = 100 kHz
R5
30k
TL082
U2
1k
R4
TL082
U3
Analog circuits – filtering and
detection
IR
DC
detect
block
Amplify
Peak
detect
Filter
Analog circuits: Filters
To understand filters you should first understand the difference
between the TIME DOMAIN and FREQUENCY DOMAIN
Which is the correct match between the following time-domain (left)
signals and their Fourier Transforms (right) ?
a)
t
i)
f
1) a-i, b-iv, c-ii, d-iii
2) a-ii, b-iv, c-iii, d-i
b)
ii)
3) a-iii, b-iv, c-i, d-ii
4) a-iv, b-ii, c-iii, d-i
c)
iii)
d)
iv)
Analog circuits: Filters
Demo: Frequency generator and Spectrum analyzer
Frequency
Generator
signal
ground
Spectrum
Analyzer
Analog circuits: Filters
“Transfer Function” = Vout/Vin = H(w)
Zcap = 1/j wC
So: Vout (w) = H(w)*Vin(w)
Zind = j wL
This is all in terms of w since, in general,
impedances are functions of w.
Zres = R
Similar to voltage divider: except w dependent.
Frequency
Generator
Vin
Z1
Vout
Z2
ground
Spectrum
Analyzer
Analog circuits: Filters
Z2
H (w ) 
Z1 + Z 2
Vout (w) = [Vin(w)/(Z1+Z2)]*Z2
So: H(w) = Z2/(Z1+Z2)
For resistors, this is just the well known
voltage divider: R2/(R1+R2)
Frequency
Generator
Vin
Z1
Vout
Z2
ground
Spectrum
Analyzer
Analog circuits: Filters
Now plug in a resistor and a capacitor:
1 / j wC
H (w ) 
R + 1 / jwC
Z2 = 1/j wC
Z1= R
1

1 + jwRC
Z1
Frequency
Generator
Vin
R1
100kk
33
Vout
C1
50 nF
100 nF
Z2
Spectrum
Analyzer
Analog circuits: Filters
1
H (w ) 
1 + jwRC
For low frequencies (small w), H = 1
For high frequencies (large w), H  0
This is a LOW PASS FILTER
At w = j/RC, (the pole of this function) H is infinite.
At the real value w = 1/RC, H begins to decrease in
amplitude.
Z1
Frequency
Generator
Vin
R1
100kk
33
Vout
C1
50 nF
100 nF
Z2
f0 = 1/(2pRC) = 30 Hz
Spectrum
Analyzer
Analog circuits: Transfer Functions
Bode plots: a graphical representation of frequency response on
logarithmic axes.
(20 is used instead of 10 so the
Vertical axis:
result will represent power ~ V2)
dBV = 20log10(|V|)
Horizontal axis:
log10(f)
-3 dB = ½ as much power as 0 dB
Vout is 1/√2 of Vin at -3dB
Log of frequency is used to ensure
linear plots from 1/f or 1/fn functions
Pole: 1/(1+jw/w0)
-20 db/decade in amplitude after w0, -90 phase
Zero: (1+jw/w0)
+20 db/decade in amplitude after w0, +90 phase
Analog circuits: Filters
Bode Plot:
1
H (w ) 
1 + jwRC
-3dB, 30 Hz
-20db/decade / pole
- 45 deg, 30 Hz
-90 deg / pole
Analog circuits: Transfer Functions
Bode plots: a graphical representation of frequency response on
logarithmic axes.
Zero at w=0
H (w )  -
Pole at w=1/(R2C2)
jwR1C2
(1 + jwR2C2 )(1 + jwR1C1 )
Pole at w=1/(R1C1)
Pole: 1/(1+jw/w0)
-20 db/decade in amplitude after w0, -90 phase
Zero: (1+jw/w0)
+20 db/decade in amplitude after w0, +90 phase
Analog circuits: Simple Pole
Bode Plot:
1
H (w ) 
1 + jwRC
-3dB, 1/RC
-20db/decade
- 45 deg, 1/RC
-90 deg
Analog circuits: Simple Zero
H (w )  1 + jwRC
Bode Plot:
+3dB, 1/RC
+20db/decade
+45 deg, 1/RC
+90 deg
Analog circuits: Filters
1
H (w ) 
1 + jwRC
Ch0
Vout
Ch1
Vin
R1
100kk
33
Vout
C1
50 nF
100 nF
Vin
f0 = 1/(2pRC) = 30 Hz
Gnd
Analog circuits: Filters
Vin
C1
Vout
R1
How does this circuit affect the following waveform:
1)
3)
2)
4)
Analog circuits: Active Filters
R1
Active Band Pass:
Z1
C1
C2
R2
Z2
1
Z 2  R2 +
jwC2
U1
TL082
1
Z1  ( + jwC1 ) -1
R1
H(w) = - Z1/Z2
Analog circuits: Active Filters
Active Band Pass:
R1
Z1
C1
C2
R2
U1
TL082
Z2
Zero at w=0
jwR1C2
H (w )  (1 + jwR2C2 )(1 + jwR1C1 )
Pole at w=1/(R2C2)
Pole at w=1/(R1C1)
Analog circuits: Active Filters
20log(|H|)
Idealized Bode Plot:
20log(R1/R2) dB
(1) (2)
(1) (2) (3)
(1)
0 dB
1/(R2C2)
1/(R1C1)
20db/decade
(1)
Zero at w=0
w
jwR1C2
H (w )  (1 + jwR2C2 )(1 + jwR1C1 )
(2)
Pole at w=1/(R2C2)
(3)
Pole at w=1/(R1C1)
Analog circuits: Active Filters
phase(H)
Idealized Bode Plot:
(1)
-90
(1) (2)
-180
(1) (2) (3)
-270
w
1/(R2C2)
1/(R1C1)
Zero at w=0
(1)
jwR1C2
H (w )  (1 + jwR2C2 )(1 + jwR1C1 )
(2)
Pole at w=1/(R2C2)
(3)
Pole at w=1/(R1C1)
Analog circuits: Active Filters
Which best describes the amplitude
response (Bode plot) of the following
transfer function (R1C1 > R2C2):
1)
(1 + jwR1C1 )
H (w ) 
(1 + jwR2C2 )
2)
0db
0db
1/ R1C1
1/ R2C2
3)
1/ R1C1
1/ R2C2
4)
0db
1/ R1C1
1/ R2C2
0db
1/ R1C1
1/ R2C2
Analog circuits – filtering and
detection
Band Pass
IR
DC
detect
block
Amplify
Filter
R1
R1
C1
R2
Low
pass
C2
U1
TL082
R1
C1
R2
C2
U1
TL082
C1
R2
C2
U1
TL082
Use multiple stages to get steeper filter roll-offs…
Htot(w) = H1(w) * H2 (w) *H3(w)
Remember –20dB/dec for each POLE
Debugging Circuits
Learn to systematically check your circuits:
• Power rails:
– Check that 15V is really 15V; if not, localize the component
that is shorting the power rail.
• Physical check:
– Check pinouts, missing/loose wires, etc.
• Isolate stages where possible
– Check output of stage 1 – if ok plug into stage 2 and see if
stage 1 output is degraded.
– If ok check output of stage 2 etc
• Keep wiring TIDY!
DISCUSSION Q: What is wrong with this circuit, when
implemented with a TL082 OP-AMP?
Vcc
+12V
Vin
+
Vcc
+12V
U1
UA741
D2
1N914
+
C1
Vee
-12V
D1
1N914
R1
Vee
-12V
U2
UA741
Vout