Download Power Electronics - HCMUT - Project Management System

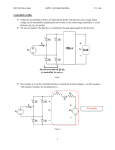
Department of Electrical and Computer Engineering
EE8410 Course Notes
Power Electronics
2006 Edition
David Xu and Bin Wu
Contents
1. Course Outline………………………………………………………………………………. 2
2. Design Projects………………………………………………………………….……………5
2.1 Project 1- DC/DC Switch Mode Power Supply ……………………………………………. 5
2.2 Project 2 – Phase Controlled Rectifier ………………………………………………………8
2.3 Project 3 – Three-phase AC Power Supply …………………………………………………10
3. Solutions to Selected Problems………………………………………………………….. 12
3.1 dc-dc Switch Mode Converters……………………………………………………………... 12
3.2 Single and Three Phase Diode Rectifiers…………………………………………………… 16
3.3 Single and Three Phase Thyristor Rectifiers………………………………………………... 21
3.4 Switch Mode Inverters……………………………………………………………………… 25
4. Examination Samples……………………………………………………………………… 29
EE8410
1
Power Electronics
1. Course Outline
Course Description
A course on microprocessor-controlled solid state converters. Major topics includes: solid state switching
devices, dc-dc switch mode converters, diode & thyristor rectifiers, current & voltage source inverters,
industry applications and microprocessor programming techniques. Typical control schemes for these
converters will also be discussed. Important concepts are illustrated with laboratory design projects. An
MC68HC11 microprocessor based MPP board will be used in the projects.
Course Organization
This course consists of three hours of lecture and two hours of laboratory per week.
Course Material
Text "Power Electronics -- Converters, Applications and Design" by N.Mohan, T.Undeland and
W.Robbins, 3rd Edition, published by John Wiley & Sons, Inc.,
Reference:
“Fundamental of Power Electronics, Second Edition” by R.W. Erickson and D. Maksimovic,
published by Springer Science+Business Media Inc.
Course Notes
"ELE8410 Power Electronics - Course Notes" by D. Xu and Bin Wu, 2006 Edition, which can be
downloaded from ELE754/EE8410 course website:
http://www.ee.ryerson.ca/~courses/ele754/downloads.htm
Course Evaluation
• Theoretical component
Mid-term Examination
Final Examination
•
55%
20%
35%
Design Pojects
DC/DC Switch Mode Power Supply
Phase Controlled Rectifiers
Three-phase AC Power Supply
45%
15%
15%
15%
Each project starts from choosing converter topology, design of passive components, developing
controllers and demonstrating the simulation results. Three semi-formal project reports are required.
EE8410
2
Power Electronics
Lecture Topics
1
dc-dc Switch Mode Converters
(pp 161-199)
1.1 Introduction
1.2 Buck converters
1.3 One-quadrant chopper
1.4 Two-quadrant chopper
1.5 Review of 68HC11 based MPP board
1.6 Microprocessor control of dc-dc converters
7 hrs
2
Microprocessor Controlled dc Motor Drives (pp 377-398)
2.1 Introduction
2.2 Equivalent circuit of dc motors
2.3 dc motor speed control
2.4 Converters used in the dc motor drives
2.5 Microprocessor control of dc motor drives
5 hrs
3
Diode and Thyristor Rectifiers
(pp 79-160)
3.1 Introduction
3.2 Single and three phase diode rectifiers
3.3 Total harmonic distortions and power factor
3.4 Single and three phase thyristor (SCR) rectifiers
3.5 Microprocessor control of thyristor rectifiers
8 hrs
4
Inverters (dc -ac converters)
(pp 200-248)
4.1 Introduction
4.2 Single-phase Inverters
4.3 Three-phase IGBT Inverters
4.4 PWM techniques
4.5 Current source Inverters
4.6 Induction Motor Speed Control (pp 399-434)
8 hrs
5
Applications
(pp 354-364, 460-504)
5.1 Introduction
5.2 Uninterruptible power supplies (UPS)
5.3 Power supplies
5.4 Motor drives
5.5 Active power filters
5.6 Static var compensators
5.7 Electronic ballasts
6 hrs
(pp 667-730)
3 hrs
6
Design Considerations
6.1 Introduction
6.2 Snubber circuit design
6.2 Gate drive circuits
6.3 Heatsink design
EE8410
3
Power Electronics
Project Schedule
Projects
Topics
Week #
Project 1 DC/DC Switch Mode Power Supply
3-6
Project 2 Phase Controlled Rectifier
7-9
Project 3 Three-phase AC Power Supply
10-12
•
Course grade
A final letter grade shall be assigned based on the following conversion table.
A+
A
AB+
B
B-
90% - 100%
85% - 89%
80% - 84%
75% - 79%
70% - 74%
66% - 69%
C+
C
CD+
D
DF
63% - 65%
60% - 62%
57% - 59%
54% - 56%
52% - 53%
50% - 51%
00% - 49%
Instructor
David Xu, PhD
Room ENG333, 245 Church Street, Toronto
Department of Electrical and Computer Engineering
Ryerson University
(416) 979-5000 ext: 6075
eMail: [email protected]
Faculty Course Survey
The faculty course survey will be held in November, 2006.
EE8410
4
Power Electronics
2. Design Projects
2.1 Project 1 DC/DC Switch Mode Power Supply
Objectives
• To review the DC/DC converters;
• To become familiar with feedback control;
• To study the performance of switch mode power supply;
Specification
• Non-isolated switch mode power supply.
• Input: 48VDC
• Output: 5VDC, 50W at full load. The minimum output current is 0.5A
• Ripple voltage over output: ≤100mV, peak-to-peak
Converter Topology
Buck converter is suggested as shown in Figure 1.
T1
+
iL
C + −E
+
G
Vd
D1
VL
−
−
Io
+ L
Vo
−
R
Figure 1 Buck converter with controller
Controller
A voltage regulator is recommended in this project as shown in Figure 2
vo ,ref
vo
Figure 2 Voltage feedback control
The regulators usually is lead-lag regulator (PID regulator), which widen the system bandwidth and
improve the phase margin.
EE8410
5
Power Electronics
Requirement
• A MATLAB/Simulink model is required to choose the parameters and verify the design.
• Choose the proper parameters for the passive components, L and C according to the specification.
Assume the passive components are ideal.
• Choose the proper parameters for lead-lag regulator, assume the triangle wave is 0-10V (peak-to-peak)
and the switching frequency is 50KHz, using simulation software.
• Following simulation results of inductor current and output voltage waveforms at different load
conditions are required in the reports.
1) Full load
2) 10% of the full load.
3) Transient procedures from 10% to 100% of the full load.
4) Transient procedures from 100% to 10% of the full load.
Questions
1) In practical design, the capacitors are not ideal. How to meet the design specification?
2) How to reduce the size of your design?
3) If the supply needs to be isolated from 48V, which topology will you recommend? Why?
Report
Each student should develop your own simulation model and write the report. The guideline of the report is
in appendix I. Submit your report with the copy of simulation model attached.
EE8410
6
Power Electronics
Appendix I
Report Writing Guidelines
Title page
This page includes: the title of the report, author name, for whom and when the report was prepared.
Abstract
An abstract is a short paragraph summarizing the report. One or two sentences for each of the following
items would be appropriate:
• Purposes (objectives)
• Methods
• Observations (figures-of-merit)
• Conclusions & recommendations
An abstract can be executive summary. The reader wants to read a short paragraph and to be able to put the
report into context with other relating materials without spending much time reading the whole report.
Thus, an abstract requires a careful preparation and is the LAST item to be written in a report. It should be
independent and the rest of the report should be written as if an abstract doesn’t exist.
Introduction
This paragraph explains the initiation of the study, the problem to be investigated, the approach or the
method to be employed for the study.
Theory
Develop all theoretical formulations or explanation for the performance of the systems under investigation.
If simulation is adopted, a paragraph of description should be given to the simulation models.
Experiments/Simulation Results
Use graphs and/or tables to show all the data. Oscilloscope tracings and/or waveform drawings should be
reported in this section. Proper calculations should also be given to verify the experimental/simulation
results.
Conclusions & Recommendations
It is important to make a precise conclusion of the project. List the major results together with short
explanations and comments. Recommendations are also necessary in a report.
References
List all the references, such as papers, books and other reports here.
Appendix, Others
• Derivations of the complex equations
• Simulation programs or simulation models
• Others tracings or waveforms.
• Materials related to the report
EE8410
7
Power Electronics
2.2 Project 2 Phase Controlled Rectifier
Objectives
• To review the AC/DC converters;
• To become familiar with feedback control of rectifier;
• To study the performance of phase controlled rectifier;
Specification
• Isolated current source power supply.
• Input: three-phase 208VAC, 60Hz.
• Output: 50A at full load.
• Ripple current over output: ≤1A, peak-to-peak
Converter Topology
Three-phase SCR rectifier is suggested as shown in Figure 3. An isolation transformer is adopted. The
transformer is 10KVA, 208V/208V Y/∆ connection. The leakage inductance is 0.02pu. The load resistance
is about 1Ω.
v
− an +
v
− bn +
v
− cn +
ia
T1
T3
T5
+
id
L
ib
vd
ic
T4
T6
T2
−
Load
R = 1Ω
Figure 3 Three-phase SCR rectifier
Controller
A feedback control is recommended in this project as shown in Figure 4
id ,ref
id
Figure 4 Current feedback control
EE8410
8
Power Electronics
In this controller, a PI regulator is adopted to regulate the output current of the three-phase SCR rectifier.
The current is smoothed by the dc inductor.
Requirement
• A MATLAB/Simulink model is required to choose the parameters and verify the design.
• Choose the proper parameters for the passive component, L according to the specification. Assume L is
an ideal inductor.
• Choose the parameters for the PI regulator.
• Following simulation results of load current and output voltage waveforms at different load conditions
are required in the reports.
1) Full load at 50A,
2) Transient procedures from no load to full load.
3) Transient procedures from full load to no load.
• Show the current waveforms of transformer’s primary and secondary side currents in your report.
Questions
1) In practical design, the transformer is not ideal. What’s the effect of the transformer leakage
inductance?
2) Which topology will you recommend to reduce the size for the current source power supply? Why?
3) How to eliminate the harmonic currents at primary side of the transformer?
Report
Each student should develop your own simulation model and write the report. Submit your report with the
simulation models attached.
EE8410
9
Power Electronics
2.3 Project 3 Three-phase AC Power Supply
Objectives
• To review the DC/AC converters;
• To become familiar with PWM;
• To study the performance of three-phase inverter;
Specification
• Three-phase AC power supply.
• Input: 400VDC,
• Output: 220VAC, rms value, 10KW at full load. The load resistance is 4.84Ω.
Converter Topology
Three-phase inverter is suggested as shown in Figure 5. Three-phase output LC filters are adopted to
smooth the output voltage. Assume the inductance of the filter is about 0.1pu and the output filter corner
frequency is 1KHz. The switching frequency is 20KHz.
Figure 5 Three-phase inverter with output filter
EE8410
10
Power Electronics
Controller
A feedback control is recommended in this project as shown in Figure 6
v A,ref
vA
vB ,ref
vB
vC ,ref
vC
Figure 6 AC current control
In this controller, three PI regulators are adopted to regulate the output voltage. The reference voltages are
three-phase sinusoidal voltages at 220V (RMS). The regulators produce the compensate voltages over the
filter inductance at full load. Due to the performance of PI regulators, parameters should be carefully
chosen since the reference is not DC value. The triangle waveform is ±10V peak-to-peak.
Requirement
• A MATLAB/Simulink model is required to choose the parameters and verify the design.
• Choose the proper parameters for the passive component, L and C according to the specification.
Assume L and C are ideal.
• Choose the parameters for the PI regulators. Assume all the three regulators are identical.
• Following simulation results of load current and output line-to-line voltage waveforms at full load
conditions are required in the reports.
• Show the current waveforms of collector current of IGBT T5 and inverter output current at phase A.
Questions
1) How to avoid the LC resonance in the output filter.
2) How to reduce the steady state error? Which control strategy would be recommended if no steady-state
error is required?
3) Analysis the relationship between inverter output voltage and load voltage at fundamental frequency,
using phasor diagram.
Report
Each student should develop your own simulation model and write the report. Submit your report with the
simulation models attached.
EE8410
11
Power Electronics
3. Solutions to Selected Problems
3.1 dc-dc Switch-mode Converters
Step-down Converters (Chapter 7, Moham)
7-1
VO=5V, Vd=10V to 40V, PO≥5W, fs=50kHz. Find the minimum inductance to keep the converter
in the continuous conduction mode under all conditions.
Solution:
For a given load and output voltage, the likelihood that the inductor current will fall to zero
is increased by lowering the duty ratio and thus increasing the OFF time. The duty ratio is
lowest when Vd=40V. PO/VO=5W/5V=IO=1A
For continuous conduction from Eq. 7 - 5,
IO ≥
D
[Vd − VO ]
2 fS L
D=
5
D
0.125
= 0.125; L =
[Vd − VO ] =
[ 40 − 5]
40
2fS I O
2 × 50000 × 1
L = 43.75 µH
7-2
Vo=5V, fs=20kHz, L=0.001H, C=470µF, Vd=12.6V, Io=0.2A. Find ∆Vo.
Solution:
Is the circuit operating in the continuous mode?
D
[Vd − Vo ] = 0.0754 where D = 5 = 0.397
From Eq.7 - 5, i OB =
2 fs L
12.6
T (1 − D )Vo
It is in the continuous mode, so from Eq.7 - 24 ∆Vo = s
8 LC
[1 − (5 12.6)]× 5
∆Vo =
= 2.01mV
2
(20,000) × 8 × 0.001 × 470 × 10 −6
2
7-3
Find the RMS ripple current through L. (optional)
Solution:
iL,ripple
0.0755
A
t
-0.0755A
DTS
(1-D)TS
TS
EE8410
12
Power Electronics
⎡ di ⎤
V = L⎢ L ⎥ ;
⎣ dt ⎦
During t on ,
di L 12.6 − 5
=
= 7600 A s
dt
0.001
di L
−5
5
=
= −5000 A s ; D =
= 0.397.
dt
0.001
12.6
Therefore, the peak - to - peak ripple current is
During t off ,
∆i L = 0.397(50 µs )(7600 A s ) = 0.151A
for 0 < t < 19.84 µs
i L ,ripple (t ) = −0.0755 + 7600t
Note : Ts = 50 µs
Note : DTs = 19.84 µs
for 19.84 µs < t < 50 µs
= 0.1747 - 5000t
T
1 s
[i L ,ripple ] 2 ∂t =i L ,ripple RMS
∫
Ts 0
RMS ripple current = 43.66mA
7-5
Calculate the ripple voltage in problem 7-2 if the load current is reduced to IOB/2. (optional)
Solution:
Vo
5
D
I o = 0.0377 A;
=
=
; ∴ ∆1 = 1.52 D
Vd 12.6 D + ∆ 1
Using Eq.7 - 14,
V T D∆
12.6 D∆1
0.1197
I o = 0.0377 = d s 1 =
; ∴ ∆1 =
,
2L
2 × 20,000 × 0.001
D
0.1197 = 1.52 D 2 ; D = 0.281.
Using the equation derived in problem7 - 4,
∆VO = 1.66mV
One-quadrant chopper
T
+
G
Vd
iT
iO
L
+
iD
R
VO
D
Ea
_
_
Fig 7-a Circuit diagram of one-quadrant chopper
7-a
EE8410
In the one-quadrant chopper circuit of Fig. 7-a, Vd=600V, Ea=200V,
Ts=4000µs, ton=2500µs. Show that the output current iO is continuous.
Solution:
13
L=4mH, R=1.5Ω,
Power Electronics
τ = 4mH 1.5Ω = 2667 µs
ton τ = 2500 2667 = 0.937
Ts τ = 4000 2667 = 1.5
600 e 0.937 − 1 200
Imin =
−
= 178.3 − 133.3 = 45A
1.5 e1.5 − 1 1.5
Since Imin > 0, iO is continuous.
7-b
For the chopper circuit of problem 7-a, determine:
(a) The average output voltage and current, VO and IO.
(b) The output current at the instant of IGBT turn-off.
Solution:
(a)
From Prob. 7 - a, current is continous.
t
VO = on V = 0.625 × 600 = 375V
T
V − Ea 375 - 200
IO = O
=
= 116.7A
R
1.5
t on 2.5 × 10-3 × 1.5
=
= 0. 9375
(b)
τ
4 × 10-3
Ts 4 × 10-3 × 1.5
=
= 1.5
τ
4 × 10-3
600 1 - e- 0.9375 200
I max =
⋅
= 179.9A
1.5 1 - e -1.5 1.5
7-c
In the chopper circuit of Fig.7-a, Vd=600V, Ea=200V, L=1mH,
ton=2500µs. Show that the output current iO is discontinuous.
Solution:
τ = 1mH 1.5Ω = 667 µs
t on τ = 2500 667 = 3.748
R=1.5Ω, Ts=4000µs, and
Ts τ = 4000 667 = 6.0
600 e 3.748 − 1 200
−
= 41 − 133 = -92A
1.5 e 6.0 − 1 1.5
Since I min < 0, i O is discontinuous.
I min =
7-d
For the chopper circuit of problem 7-c, determine:
(a) The average output voltage and current, VO and IO.
(b) The output current at the instant of commutation.
(a)
Solution:
τ=
t on
τ
L 10 -3
=
s
R 1.5
= 2.5 × 1.5 = 3.75
10 -3
600 − 200
ln { e 3.75 [1 +
(1 − e −3.75 ) ] }
1.5
200
= 3.222 × 10 -3 s
tx =
EE8410
14
Power Electronics
VO =
(b)
7-e
2 .5
(4 - 3.222)
× 600 +
× 200 = 413.9V
4
4
V − Ea 413.9 − 200
IO = O
=
= 142.6A
1 .5
R
I max =
600 - 200
(1 - e-3.75 ) = 260.4A
1.5
In the chopper circuit of Fig. 7-a, Vd=600v, Ea=350V, R=0.1, Ts=1800µs, and L is of so large a value
that the output current may be assumed constant or ripple-free. If the output current is to be
IO=100A:
(a) Calculate the required value of ton.
(b) Sketch to scale the time variations of vG, vO, iO, iD and iT.
Solution:
VO − Ea
A
R
VO = 0.1 × 100 + 350 = 360 V
IO =
(a)
ton =
VO =
ton
Vd
T
V
360 × 1.8 × 10− 3
= 1.08 × 10 - 3 s
600
(b)
vG
vO
t on
Ts
t
600
360
t
iO
100
t
iD
100
t
iT
100
t
EE8410
15
Power Electronics
3.2 Single and Three phase Diode Rectifier
5-1 (Chapter 5, Moham)
Source voltage
v s (t ) = Vˆs sin ωt
Differential equation (assuming that the diode is on)
di
Ri + L = Vˆs sin ωt
dt
from which
V̂
di R
+ i = s sinωt
L
dt L
Adding the forced response and the natural response,
i = Ae
R
t
L
+
V̂s
sin (ωt - Φ )
Z
Z = R 2 + (ωL ) ,
2
where
( ) ( )
Initially at t = 0, i 0 - = i 0 +
previous equation : 0 = A +
∴ A=
⎛ ωL ⎞
Φ = tan -1 ⎜
⎟ and A is the coefficient to be determined.
⎝ R ⎠
= 0 . We will use this initial condition to calculate A in the
V̂s
sin (− Φ )
Z
V̂s
⎛ ωL ⎞
sin Φ = Vˆs ⎜ 2 ⎟
Z
⎝Z ⎠
Vˆ ωL
∴ i(t ) = s 2 e
Z
R
t
L
+
Vˆs
sin (ωt − Φ )
Z
5-3
v = Vd + 2V1 cos ω1t + 2V1 sin ω 1t + 2V3 cos ω 3t
i = I d + 2 I 1 cos ω1t + 2 I 3 cos(ω 3t − Φ 3 )
(a )
P = Vd I d + 2V1 I 1 cos 45° + V3 I 3 cos Φ 3
(b )
V = Vd +
2
2
(
2V1
2
I = I d + I1 + I 3
(c )
PF =
P
=
VI
)
2
+ V3
2
2
Vd I d + 2V1 I 1 cos 45° + V3 I 3 cos Φ 3
2
Vd +
(
2V 1
)
2
2
2
2
+ V3 × I d + I 1 + I 3
2
Note :
2V1 cos ω 1t + 2V1 sin ω 1t
= 2V1 (cos ω 1t + sin ω 1t )
= 2 × 2V1 sin(ω 1t + 45°)
= 2V1 sin(ω 1t + 45°)
EE8410
where 2V1 is peak value.
16
Power Electronics
5-4
(a )
v s : Sinusoidal, Vs = 120V
∴
Vd = 0.9Vs = 108V
Pd = Vd I d = 1080W
(b)
vs
200V
0
60°
120°
vd
120°
0
180°
Vd =
ωt
60°
120°
60°
200V
ωt
(200 × 120 ) + (0 × 60 ) = 200 × 2 = 133.33V
o
o
3
180 o
Pd = Vd I d = 1333.3W
5-6
I D (avg ) =
I D (rms ) =
Id
2
2
Id
I
= d
2
2
5-10
VS
200
ωt
|VS|
200
160
ωt
id
2π/3
EE8410
π
5π/3
ωt
2π
17
Power Electronics
id (0) = 0
0 < ωt <
← see " hint".
2π
3
did
= 200 − 160 = 40
dt
di d
40
40
=
=
d(ωt ) ωLs 377 × 10 −3
Ls
∴
2π
⎛
i d ⎜ ωt =
3
⎝
ωt >
2π
3
( )
2π
⎞ 40 ×
3 = 222.2 A
=
⎟
−3
⎠ 377 × 10
did
= −160
dt
di d
160
∴
== -424.4 A
rad
d(ωt )
377 × 10 -3
222.2
∴ i d comes down to zero in
= 0.523 rad ≅ 30 o
424.4
and it stays at zero until ωt = π .
Ls
5-11
Calculateθ b
2Vs sinθ b = Vd
⎛ 150V ⎞
∴ θ b = sin -1 ⎜
⎟ = 1.084 rad.
⎝ 2 × 120V ⎠
Derive i d (θ )
i d (θ ) =
1
ωL s
=
1
ωL s
i d (θ ) =
1
ωL s
θ
∫θ
b
v L dθ
θ
∫θ (
)
2Vs sin θ − Vd dθ
b
[
]
2Vs (− cosθ + cosθ b ) − Vd (θ − θ b )
∴ i d (θ ) = -450.1cosθ - 397.9θ + 641.8
Calculate θ f
i d (θ f ) = 0 = -450.1cosθ f - 397.9θ f + 641.8
cosθ f + 0.884θ f = 1.426
∴ θ f = 2.56 rad
Calculate I d,peak
The peak current occurs at (π - θ b ) since v L is positive
between θ b and π - θ b .
I d, peak = i d (π - θ b ) ;
π - θ b = 2.058 rad
∴ I d,peak = -450.1cos(2.058) - (397.9 ) × (2.058) + 641.8 = 33.6A
EE8410
18
Power Electronics
5-14
I s (rms ) = I d
From Fourier analysis :
4
I s1 (rms ) =
2 I d = 0.9 I d
π
DPF angle Φ 1 = 0
2
0
I s − I s1
0 THDis = 100
2
I s1
= 100 ×
1 − 0.9 2
= 48.4 0 0
0.9
DPF = 1.0
I
PF = s1 DPF = 0.9
Is
CF =
I s,peak
I s (rms )
=1
5-23
I D (avg ) =
Id
120 o
I
=
d
3
360 o
I D (rms ) =
Id
I
= d
3
3
2
5-27
i s is odd and quarter - wave symmetric.
Therefore, from Table 3 - 1
a n = 0 for all n,
bn =
4
π
∫
90
o
0
b n = 0 for all even n and,
i s sin (nωt )d (ωt ) for all odd n.
for 0 < ωt < 30 o ,
is = 0
30 o < ωt < 60 0 ,
4I d
is = I d
30
4I d
ω
ω
ω
(
)
(
)
(
)
∴ bn =
sin
=
cos
n
t
n
t
d
t
π ∫30o
πn
90 o
4I
= d [cos(30n )° − cos(90n )°]
n = odd
πn
Quautity within the bracket :
o
90 o
3
2
= 0
[cos(30n )° − cos(90n )°] =
∴
EE8410
bn =
4
π
×
3 Id 2 3
× =
Id
2
n
πn
for n = 1,5,7,11,13,L
for all other odd n
for n = 1 and 6n ± 1 where n = 1,2,3, L
19
Power Electronics
From Eq. 3 - 21
⎡ 1
⎤
I d ⎢∑ sin (nωt )⎥
π
⎣ n
⎦
i s (t ) =
2 3
∴
i s1 (t ) =
2 3
∴
Φ1 = 0
π
I d sin ωt
for n = 1
DPF = 1.0
and
(Eq. 5 - 72 )
1 ⎛2 3 ⎞
6
⎜
⎟=
I
d
⎟ π Id
2 ⎜⎝ π
⎠
1
(Eq. 5 - 71)
=
n
(Eq. 5 - 70)
I s1 =
I sn
I s1
I s = I s1 + ∑ I sn
2
2
2
2
⎛ 6 ⎞ ⎡
1⎞ ⎤
⎛
I d ⎟⎟ ⎢1 + ∑ ⎜ ⎟ ⎥
= ⎜⎜
⎝ π
⎠ ⎢⎣ n =5 ⎝ n ⎠ ⎦⎥
=
6
π
PF = DPF
EE8410
1
= 0.816I d
2
n =5 n
Id 1+ ∑
I s1
= 0.955
Is
(Eq. 5 - 69)
(Eq. 5 - 73)
20
Power Electronics
3.3 Single and Three Phase Thyristor Rectifiers
6-3 (Chapter 6, Moham)
vs
Vm
π
ωt
2π
Vm
vd
A1
Vm
α
π+α
π
T1 and T2 on
v d = Vm − A1
π
T3 and T4 on
(
)
= Vm − 2α Vm
(
2α
π = Vm 1 − π
At α = 45°, v d = 100V
ωt
2π
)
At α = 135°, v d = −100V
6-5
(a )
Vdo = 0.9 Vs
π
2 Vs
α
π
Vdα = 2 Vs ∫ sin ωt d(ωt ) π =
DPF = cos(α 2)
[cosα + 1]
180° - α
180°
can be calculated by equating power : Vs I s1 ⋅ DPF = Vdα I d
Is = Id
I s1
I s1 =
(b )
1
Vdα = Vdo
2
2 ⋅ Vs
(1 + cosα ) = 1 × 0.9 ⋅ Vs
π
2
π × 0.9
−L
cosα =
2 2
α = 90°
∴
or
∴
∴
EE8410
Vdα I d
Vs cos(α 2 )
∴
DPF = cos(α 2 ) = 0.707
21
Power Electronics
180 − 90
= 0.707 I d
180
0.5 × 0.9Vs
I s1 =
I d = 0.636 I d
Vs cos(90° 2 )
Is = Id
∴
PF =
I s1
⋅ DPF = 0.636
Is
2
THDi =
(c )
I s − I s1
(d )
6-6
6-7
%=
I s1
0.707 2 − 0.636 2
% = 48.55%
0.636
In a full - bridge converter,
(Eq. 6 - 6)
Vdα = Vdo cos α
∴
2
α = 60°
for Vdα = 0.9Vo ,
DPF = cos α = 0.5 (Eq. 6 - 16 )
PF = 0.9 cos α = 0.45 (Eq. 6 - 17 )
THDi = 48.43%
Comparision of (b) and (c) shows
that the Power Factor is better in the half - controlled converter
I thy (avg ) 1
I thy (rms )
1
= ,
=
Id
Id
2
2
Pd = 1 KW , I d = 10 A, i d ≅ I d , Vs = 115V (+ 5%, - 10% )
Calculate L s :
ω = 2π × 60 = 377 rad s
Transformer VA = 1500VA
rated Vpri = 120V ,
rated I pri = 1500
Z base =
V pri
I pri
120
= 12.5 A
(rated ) = 9.6Ω
ωLs = (8% ) Z base
or
L s = 0.08 × 9.6 377 ≅ 2mH
α cannot go below 0!
Therefore, to calculate the minimum transformer turns ratio a (where a =
V pri
Vsec
),
0.9
2
Vs cos α − ω (Ls )I d
π
a
Substitute Vd = 100V , α = 0° and Vs, min = 115V (− 10% ) = 103.5V
in Eq. 6 - 26, Vd =
∴
From the above equation, a min = 0.89
With a min and Vs = 115V (+ 5% ) = 120.75V ,
the above equation yields α = 31° for Vd = 100V .
EE8410
22
Power Electronics
6-11
3ωLs
Vd = Vdo cos α −
π
cos(α + u ) = cos α −
Vdo =
3 2
π
(Eq. 6 - 55)
Id
2ωLs
2VLL
I d (Eq. 6 - 62)
(Eq. 6 - 36)
VLL
Replacing (ωL s I d ) in Eq. 6 - 55 by Eq. 6 - 62,
3
2
V
V [cos α − cos(α + u )] = Vdo cos α − do [cos α − cos(α + u )]
2
π 2 LL
∴ Vd = Vdo cos α −
∴ Vd =
∴
Vdo
2
[cosα + cos(α + u )]
Vdo I d
[cos α + cos(α + u )]
2
On the ac side, ac power is Pac = 3V LL I s1 cos φ1
dc power Pd = Vd I d =
Approximation : I s1 ≅
6
π
Id
(Eq. 6 - 44)
The above equation is approximate because the above equation is correct only if L s = 0
(and hence u = o).
∴
Pac ≅ 3VLL
6
π
I d cos φ1
Equating Pac = Pdc
3V LL
∴
6
π
I d cos φ1 ≅
DPF = cos φ1 ≅
3 2
π
V LL
Id
[cosα + cos(α + u )]
2
1
[cosα + cos(α + u )]
2
6-12
VLL = 460V , f = 60Hz, ω = 377 rad , L s = 25µH , Vd = 525V , and Pd = 500kW .
s
Pd 500 × 1000
=
= 952.4 A
Id =
525
Vd
Vd = 1.35V LL cos α −
3ωL
π
Id
⎛ 3 × 377
⎞
525 + ⎜
× 25 × 10 −6 × 952.4 ⎟
π
⎝
⎠
∴ cos α =
1.35 × 460
∴ α = 30.77°
cos(α + u ) = cos α −
2ωLs
2V LL
I d = 0.859 −
2 × 377 × 25 × 10 −6
2 × 460
× 952.4
= 0.831
or
(α + u ) = 33.76°
Therefore, the commutation angle u is
u = 33.76° - 30.77° ≅ 3°
EE8410
23
Power Electronics
6-a
EE8410
Consider the 3φ full bridge thyristor rectifier shown in Fig.6-19 (page 138).
Draw waveforms of VPn , VNn and Vd at α=30°, 90° and 150°.
24
Power Electronics
3.4 Switch Mode Inverters
8-a
(Chapter 8, Moham)
The single-phase half-bridge inverter in Fig.8-4 has a resistive load of R=2.4Ω and the dc input
voltage is Vd=48V. Consider square wave operation with device conduction angle of 180° per
cycle. Determine
(a) the rms output voltage Vo1 at the fundamental frequency;
(b) the average output power Po;
(c) the peak and average currents of each transistor; and
(d) the total voltage harmonic distortion.
Solution:
(a ) Fourier series
vo =
∞
2Vd
sin( nωt )
n=1, 3, 5L nπ
∑
Vo1 = 0.45 × 48 = 21.6 V
(b)
Po =
(c )
1 T 2
vo dt = 24 V
T ∫0
Vo =
Vo2
I Peak =
R
Vd
= 240 W
= 10 A
2R
Duty cycle = 50%
I avg = 0.5 ×10 = 5 A
Vo2 − Vo21
=
Vo1
(d ) THD =
8-b
24 2 − 21.6 2
= 0.48
21.6
Repeat Problem 8-a for a single phase bridge inverter in Fig.8-11.
Solution:
(a)
Fourier series
vo =
∞
4Vd
sin(nωt )
n =1, 3, 5L nπ
∑
Vo1 = 0.9 × 48 = 43.2 V
(b)
Po =
(c )
EE8410
Vo2
I Peak =
Iavg
(d )
1 T 2
vo dt = 48 V
T ∫0
Vo =
R
Vd
= 960W
= 20 A
R
= 0.5 × 20 = 10 A
Vo2 − Vo21
THD =
= 0.48
Vo1
25
Power Electronics
8-c
The single phase full bridge inverter in Fig.8-11 has an RLC load with R=10Ω, L=31.5mH, and
C=112µF. The inverter frequency fo = 60Hz and dc input voltage Vd = 220V. Consider the square
wave operation with device conduction angle of 180° per cycle.
(a) Express the instantaneous load current in Fourier series;
(b) Calculate the rms load current I1 at the fundamental frequency;
(c) Calculate the THD of the load current;
(d) Calculate the power absorbed by the load Po and the fundamental power Po1; and
(e) Calculate the average current of dc supply Id.
Solution:
The inductive reactance for the nth harmonic voltage is
X L = j 2nπ × 60 × 31.5 × 10 −3 = j11.87n Ω
The capacitive reactance for the nth harmonic voltage is
j10 6
− j 23.68
=
Ω
2nπ × 60 × 112
n
The impedance for the nth harmonic voltage is
XC = −
[
Z n = 10 2 + (11.87n − 23.68 n)
]
2 12
and the power factor angle for the nth harmonic voltage is
θ n = tan −1
(a )
11.87n − 23.68 n
2.368 ⎞
⎛
= tan −1 ⎜1.187n −
⎟
n ⎠
10
⎝
The instantaneous output voltage can be expressed as
v o (t ) = 280.1sin(337t ) + 93.4 sin(3 × 377t ) + 56.02 sin(5 × 337t )
+ 40.02sin(7 × 377t ) + 31.12 sin(9 × 377t ) + L
Dividing the output voltage by the load impedance and considering the appropriate delay
due to the power factor angles, we can obtain the instantaneous load current as
(
)
(
)
+ sin(5 × 377t - 79.63 ) + 0.5 sin(7 × 377t − 82.85 )
+ 0.3sin(9 × 377t - 84.52 ) + L
i o (t ) = 18.1sin 377t + 49.72o + 3.17 sin 3 × 377t − 70.17 o
o
o
o
(b)
I o1 = 18.1
2 = 12.8 A
(c)
Consider up to the ninth harmonic.
I o = I o21 + I o23 + L + I o29 = 13.02
THD =
(d)
I o2 _ I o21
I o1
= 18%
Po = I o2 R = 1695 W
Po1 = I o21 R = 1638.4 W
(e)
EE8410
I d = Po Vd = 7.7 A
26
Power Electronics
Repeat Problem 8-c assuming that C = 0.
8-d
The solution to this problem is not provided.
8-e
In the single phase full bridge PWM inverter circuit of Fig.8-11, Vd = 300V, ma =0.8, mf = 39 and
the frequency of the sine modulating wave is 60Hz. The load resistance is 10Ω and load inductance
is 1mH. Bipolar modulation technique is used. Determine
(a)
switching frequency of each transistor;
(b)
the rms values of voltage and current at the fundamental frequency;
(c)
the rms values of 37th and 39th harmonic voltages and currents; and
(d)
the ratio of 39th harmonic current to fundamental current.
Answers:
(a)
f sw = 60 Hz × 39 = 2340 Hz
(b)
From Table 8 - 1, the rms voltage of fundamental is
0.8Vd
V
169.7
Vo1 =
= 169.7V
I o1 = o1 =
= 16.96 A
ZL1 10 + j 2 × π × 60 × 0.001
2
(c )
Vo37 =
0.22Vd
= 46.67V
2
Vo39 =
0.818Vd
= 173.52V
2
(d )
I o37 =
Vo37
46.67
=
= 2.719 A
ZL37 10 + j 2 × 37 × π × 60 × 0.001
I o39 =
Vo39
173.52
=
= 9.759 A
ZL39 10 + j 2 × 39 × π × 60 × 0.001
I o39 Io1 = 0.575
8-f
Consider a 3Φ inverter in Fig.8-21. Assume that IGBTs are used as switching devices. The
conduction angle of each IGBT is 180o per cycle.
(a)
Draw waveforms of IGBT gate signals, line-to-line and line-to-neutral voltages of the
inverter.
(b)
Derive an expression for the calculation of rms values of line-to-line and line-to-neutral
voltages.
(c)
Derive an expression for the calculation of rms values of fundamental components of lineto-line and line-to-neutral voltages.
8-g
The three-phase inverter in Fig.8-21 has a wye-connected load of R = 5Ω and L = 23mH. The
inverter frequency is fo= 60Hz and the dc input voltage is Vd = 220V. The conduction angle of each
switching device is 1800 per cycle.
(a)
Express the instantaneous line-to-line voltage vab(t) and line current ia(t) in a Fourier series.
(b)
Determine the rms line voltage VL ;
(c)
Calculate the rms phase voltage VP;
(d)
Calculate the rms line voltage VL1 at the fundamental frequency;
(e)
Calculate the rms phase voltage at the fundamental frequency, VP1;
(f)
Determine the total harmonic distortion THD of line current ia;
(g)
Determine the load power Po; and
(h)
Determine the average dc current Id.
Solution (continued on next page):
EE8410
27
Power Electronics
(a ) Refer to your class notes. The instantaneous line - to - line voltage v ab (t ) can be written as
v ab (t ) = 242.58 sin (337t + 30°) − 48.52 sin 5 × (377t + 30°)
− 34.66 sin 7 × (377t + 30 o ) + 22.05sin 11 × (337t + 30 o )
+ 18.66 sin 13 × (377t + 30 o ) − 14.27 sin 17 × (377t + 30o ) + L
Z L = R 2 + (nωL ) ∠ tan −1 (nωL R ) = 5 2 + (8.67 n ) ∠ tan −1 (8.67 n 5)
2
2
i a (t ) = 14 sin(377t − 60 o ) − 0.64 sin(5 × 377t − 83.4 o )
− 0.33 sin(7 × 377t − 85.3o ) + 0.13 sin(11 × 377t − 87 o )
+ 0.10 sin(13 × 377t − 87.5o ) − 0.06 sin(17 × 377t − 88o ) − L
(b) VL = 0.8165 × 220 = 179.63 V .
(c) Vp = 0.4714 × 220 = 103.7 V .
(d ) VL1 = 0.7797 × 220 = 171.53 V .
(e) Vp1 = VL1
(f)
= 99.03 V .
3
Consider up to 17th harmonic.
(0.64
THD =
)
1
+ 0.332 + 0.132 + 0.10 2 + 0.06 2 2
= 0.053
14
( g ) For wye - connected loads, the line current is the same as the phase current. The rms line current is
(14
=
2
)
1
+ 0.64 2 + 0.332 + 0.132 + 0.10 2 + 0.06 2 2
IL
= 9.91 A
2
The load power Po = 3I L2 R = 3 × 9.912 × 5 = 1473 W .
2
(h) The average dc current I d = Po 220 = 1473 220 = 6.7 A.
8-h
The three phase inverter in Fig.8-21 operates in a PWM mode. A three phase wye-connected load
of R = 10Ω and L = 2mH is connected to the inverter. The input dc voltage is 240V. The gating
pattern is sinusoidally modulated with ma = 1.0 and mf = 21. The fundamental frequency is 100Hz.
Determine:
(a)
the rms values of fundamental voltage and current;
(b)
the rms values of 5th and 7th harmonic voltages and currents; and
(c)
the rms values of 19th and 23rd harmonic voltages and currents.
The solution to this problem is not provided.
EE8410
28
Power Electronics
4. Examination Samples
MIDTERM EXAMINATION
ELE 754 Power Electronics
Ryerson University
Department of Electrical and Computer Engineering
Duration: 2 hours
Instructor:
Dr. B.Wu
Instructions:
1. Answer all four questions.
2. Show details of your derivations/calculations.
Marks:
Q1. 30%
______________
Q2. 20%
______________
Q3. 30%
______________
Q4. 20%
______________
Student Name:
_________________________________
Student Number: _________________________________
Question 1 (30%)
EE8410
29
Power Electronics
iT
T
+
iO
+
iD
G
R
D
Vd
Vo
Ea
-
-
Fig. 1 One quadrant chopper with a dc motor load
An IGBT-based one quadrant chopper is used to drive a dc motor, whose armature circuit parameters are
represented by the winding resistance R (0.2 Ohms), winding inductance L (0.25mH) and back emf as
shown in Fig.1. The input dc voltage of the chopper is 115V and its switching frequency is 500Hz. When
the duty cycle of the chopper is 0.4, the motor runs at 1200rpm with its emf of 55V. Answer Questions 1.1
to 1.3.
1.1) The peak value of armature current.
3%
1.2)
L 0.25 × 10 −3
=
= 1.25 × 10 −3 ,
0.2
R
V − Ea
(1 − e −ton / τ )
I o, peak = d
R
115 − 55
=
(1 − e − 0.64 ) = 141.8 A
0 .2
τ=
t on = 0.4 ×
t on / τ = 0.64
Ts
τ
115 e0.64 − 1 55
×
−
= −144.6 A
0.2 e1.6 − 1 0.2
I o ,min =
3%
⎧
⎡ 115 − 55
t x = 1.25 × 10 −3 ln ⎨e 0.64 ⎢1 +
1 − e −0.64
55
⎣
⎩
2ms
= 1 .6
1.25ms
← discontinuous mode
(
= 1.25 × 10 −3 ln(2.874)
= 1.32ms
0 .8
2 − 1.32
Vo ,dc = 115 ×
+ 55
= 64.7V
2
2
EE8410
=
The average (dc) armature voltage and armature (dc) current.
3%
1.3)
1
= 0.8 × 10 −3 sec
500
)⎤⎥ ⎫⎬
⎦⎭
I o, dc =
64.7 − 55
= 48.5 A
0 .2
Sketch to scale the waveforms of vo and io, indicating the peak values.
30
Power Electronics
3%
Vo
115V
tx
iO
141.8V
Question 1 (continued)
An external dc choke of 6mH is connected in series with the armature winding of the above mentioned dc
motor. The duty cycle is adjusted to 0.5 and the motor runs at 1120rpm. The field winding current remains
unchanged. Find:
1.4) The dc component (average value), fundamental component (peak value) and third harmonic (pick
value) in.
3%
Vo,dc = ________
3%
Vo1, peak = ________
3%
Vo3, peak = ________
Check: continuous or discontinuous mode?
L 6.25 × 10 −3
=
= 31.25 × 10 −3 ,
0.2
R
1 .0
t on / τ =
= 0.032
31.25
τ=
I o ,min =
t on = 0.5 × 2ms = 1.0ms
Ts
τ
=
2ms
= 0.064
31.25ms
115 e 0.032 − 1 51.33
×
−
= 26.25 A ← continuous mode
20 e 0.064 − 1 0.2
Ea =
55
× 1120 = 51.33
1200
Vo
Vd
Use Fourier Series to find Vo,dc, Vo1, peak and V03, peak
EE8410
31
Power Electronics
1.5)
The dc component (average value), fundamental component (peak value) and third harmonic (peak
value) in io.
= ________
3%
Io,dc
3%
Io1, peak = ________
3%
Io3, peak = ________
Vo
115V
π
Vo =
115
+
2
ωt
2π
10
∑
n = 1 , 3 , 5 ...
4 × 57 . 5
sin( n ω t )
nπ
= 57.5 + 73.21sin ωt + 24.4 sin 3ωt + 14.64 sin 5ωt + ...
↑dc
I o, dc =
I o1, peak
↑1st
↑3rd
57.5 − 51.33
= 30.82 A
0.2
73.21V
73.2
= 3.73 A
=
=
R 2 + ωL2
0.2 2 + (2π × 500 × 6.25 ×10 −3 ) 2
I o3, peak =
24.4
0.2 + (2π × 3 × 500 × 6.25 ×10 −3 ) 2
2
= 0.414 A
Question 2 (20%)
The input terminals of a single phase full bridge diode rectifier are connected to a single phase ac voltage
source rated at 208V and 400Hz with a source inductance of 4%. The rectifier is rated at 20kVA. The load
of this rectifier is an ideal dc voltage source of 240V. Answer the following questions:
2.1)
4%
Find the value of source inductance in mH.
2.2)
4%
Derive an expression for the calculation of output dc current.
EE8410
32
Power Electronics
2.3)
6%
Sketch to scale the waveforms of input voltage, dc voltage, dc current, and the voltage on source
inductance.
2.4) Calculate the diode conduction angle per half cycle of the input line frequency.
6%
Solutions:
2.1)
vs
15000
I rated =
= 72.12 A
294V
208
208
Z rated =
= 2.884Ω
θb
θp
72.12
id
383.2A
2.884
Lrated =
= 1.148mH
use equ (1)
2π × 400
θf
L = 0.04 × 1.148 = 45.9 × 10 − 6 H
vL
294V - 240V = 54V
2.2)
θ b = sin −1
240
= 54.67° = 0.945rad
2 × 208
θ p = π − θ b = 2.187rad
[
1
2 × 208(− cos θ + cos 0.954 ) − 240(θ − 0.954)
2π × 400 × 45.9 × 10 −6
id = 8.668(−294.1 cos θ + 170.1 − 240θ + 228.96)
id =
]
id = −2549 cos θ − 2080θ + 3459 A......................equ (1)
2.4)
θf = ?
− 2549 cosθ f − 2080θ f + 3459 = 0
cosθ f + 0.816θ f = 1.357
Try θf = 2.6
Try θf = 2.8
Try θf = 2.82
cosθ + 0.816θ = 1.265
cosθ + 0.816θ = 1.342
cosθ + 0.816θ = 1.352
conduction angle: θf - θ = 2.82 – 0.954 = 1.866 rad = 106.9°
EE8410
33
Power Electronics
Question 3 (30%)
A three-phase full bridge SCR rectifier without a freewheeling diode is connected to a three phase balanced
voltage source of 60Hz, 208V (line to line). Assume the load of the rectifier is a constant current source of
100A and its firing (daley) angle is 60 degrees. Find:
3.1) The average dc output voltage of the rectifier.
6%
Vd = 1.35 × 208 × cos α = 140.4V
at which α is 60°
3.2
12%
The total harmonic distortion of the input current and overall input power factor.
Ia =
1
2π
2π
∫i
a
2
dωt = 0.816 I d = 81.6 A
0
ia = 1.1I d sin(ωt − α ) − 0.22 I sin 5(ωt − α ) + ...
THD =
1.1I d
= 77.78 A
2
1
DF =
= 0.995 ,
1 + THD 2
PF = DF × DPF = 0.478
I a1 =
3.3
6%
2
I a − I a1
I a1
2
2
= 31%
DPF = cos α = 0.5
Use Fig.2 given below, draw the dc output waveform assuming that the delay angle remains at 60
degrees.
α
α
EE8410
34
Power Electronics
3.4
If a freewheeling diode is connected in parallel with the dc current source, draw the dc output
waveform assuming that the delay angle remains at 90 degrees
6%
α
α
Question 4 (20%)
4.1) List four switching devices that are commonly used in power electronic converters.
IGBT, GTO, MOSFET, SCR
4.2) Indicate which of the switching devices you have listed are voltage controlled devices and which
are current controlled devices.
IGBT, MOSFET →Voltage Controlled Devices
SCR, GTO → Current Controlled Devices
4.3) Draw a typical circuit diagram of an IGBT-based two quadrant chopper.
+
Vd
LOAD
-
4.4)
Draw a curve which illustrates the relationship between the boundary current and the duty cycle D
of a buck converter.
IBD
D
4.5)
Write an equation which describes a dynamic relationship between motor speed, electromagnetic
dω m
J
= Te − TL − Bω m
torque and load torque.
dt
In the following multiple-choice questions, circuit one best answer.
4.6)
EE8410
In a single phase, single diode rectifier with an RL load, the diode conduction angle is
a) grater than 180°.
b) less than 180°.
c) equal to 180°.
d) grater than 120°.
e) less than 120°.
f) equal to 120°.
g) grater than 60°.
h) less than 60°.
i) equal to 60°.
j) none of the above.
35
Power Electronics
4.7)
In a three-phase, full SCR bridge rectifier with a three RL load where L is assumed very large, the
delay angel is 60 degrees. The SCR conduction angle is
a) grater than 180°.
b) less than 180°.
c) equal to 180°.
d) grater than 120°.
e) less than 120°.
f) equal to 120°.
g) grater than 60°.
h) less than 60°.
i) equal to 60°.
j) none of the above.
4.8)
In a three-phase, full SCR bridge rectifier with
SCR conduction angle is
a) grater than 180°.
b) less than 180°.
d) grater than 120°.
e) less than 120°.
g) grater than 60°.
h) less than 60°.
4.9)
a three R load, the delay angel is 60 degrees. The
c) equal to 180°.
f) equal to 120°.
i) equal to 60°.
j) none of the above.
The maximum voltage and current ratings of a single IGBT device currently available in the market
are
a) 600A, 1000V b) 600A, 2000V c) 600A, 4500V d) 600A, 6500V
e) 1200A, 1000V f) 1200A, 2000V g) 1200A, 4500V h) 1200A, 6500V
4.10) The source inductance between an ideal voltage source and three phase SCR rectifier
a) may be used to assist SCR commutation
b) may increase input current THD
c) may reduce the dc output voltage
d) may increase the dc output voltage
d) none of the above.
EE8410
36
Power Electronics