* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Power Electronics - HCMUT - Project Management System
Index of electronics articles wikipedia , lookup
Standing wave ratio wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
Integrating ADC wikipedia , lookup
Schmitt trigger wikipedia , lookup
Operational amplifier wikipedia , lookup
Audio power wikipedia , lookup
Radio transmitter design wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Valve audio amplifier technical specification wikipedia , lookup
Power MOSFET wikipedia , lookup
Current source wikipedia , lookup
Surge protector wikipedia , lookup
Voltage regulator wikipedia , lookup
Current mirror wikipedia , lookup
Opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
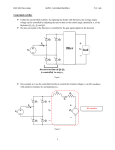
Department of Electrical and Computer Engineering EE8410 Course Notes Power Electronics 2006 Edition David Xu and Bin Wu Contents 1. Course Outline………………………………………………………………………………. 2 2. Design Projects………………………………………………………………….……………5 2.1 Project 1- DC/DC Switch Mode Power Supply ……………………………………………. 5 2.2 Project 2 – Phase Controlled Rectifier ………………………………………………………8 2.3 Project 3 – Three-phase AC Power Supply …………………………………………………10 3. Solutions to Selected Problems………………………………………………………….. 12 3.1 dc-dc Switch Mode Converters……………………………………………………………... 12 3.2 Single and Three Phase Diode Rectifiers…………………………………………………… 16 3.3 Single and Three Phase Thyristor Rectifiers………………………………………………... 21 3.4 Switch Mode Inverters……………………………………………………………………… 25 4. Examination Samples……………………………………………………………………… 29 EE8410 1 Power Electronics 1. Course Outline Course Description A course on microprocessor-controlled solid state converters. Major topics includes: solid state switching devices, dc-dc switch mode converters, diode & thyristor rectifiers, current & voltage source inverters, industry applications and microprocessor programming techniques. Typical control schemes for these converters will also be discussed. Important concepts are illustrated with laboratory design projects. An MC68HC11 microprocessor based MPP board will be used in the projects. Course Organization This course consists of three hours of lecture and two hours of laboratory per week. Course Material Text "Power Electronics -- Converters, Applications and Design" by N.Mohan, T.Undeland and W.Robbins, 3rd Edition, published by John Wiley & Sons, Inc., Reference: “Fundamental of Power Electronics, Second Edition” by R.W. Erickson and D. Maksimovic, published by Springer Science+Business Media Inc. Course Notes "ELE8410 Power Electronics - Course Notes" by D. Xu and Bin Wu, 2006 Edition, which can be downloaded from ELE754/EE8410 course website: http://www.ee.ryerson.ca/~courses/ele754/downloads.htm Course Evaluation • Theoretical component Mid-term Examination Final Examination • 55% 20% 35% Design Pojects DC/DC Switch Mode Power Supply Phase Controlled Rectifiers Three-phase AC Power Supply 45% 15% 15% 15% Each project starts from choosing converter topology, design of passive components, developing controllers and demonstrating the simulation results. Three semi-formal project reports are required. EE8410 2 Power Electronics Lecture Topics 1 dc-dc Switch Mode Converters (pp 161-199) 1.1 Introduction 1.2 Buck converters 1.3 One-quadrant chopper 1.4 Two-quadrant chopper 1.5 Review of 68HC11 based MPP board 1.6 Microprocessor control of dc-dc converters 7 hrs 2 Microprocessor Controlled dc Motor Drives (pp 377-398) 2.1 Introduction 2.2 Equivalent circuit of dc motors 2.3 dc motor speed control 2.4 Converters used in the dc motor drives 2.5 Microprocessor control of dc motor drives 5 hrs 3 Diode and Thyristor Rectifiers (pp 79-160) 3.1 Introduction 3.2 Single and three phase diode rectifiers 3.3 Total harmonic distortions and power factor 3.4 Single and three phase thyristor (SCR) rectifiers 3.5 Microprocessor control of thyristor rectifiers 8 hrs 4 Inverters (dc -ac converters) (pp 200-248) 4.1 Introduction 4.2 Single-phase Inverters 4.3 Three-phase IGBT Inverters 4.4 PWM techniques 4.5 Current source Inverters 4.6 Induction Motor Speed Control (pp 399-434) 8 hrs 5 Applications (pp 354-364, 460-504) 5.1 Introduction 5.2 Uninterruptible power supplies (UPS) 5.3 Power supplies 5.4 Motor drives 5.5 Active power filters 5.6 Static var compensators 5.7 Electronic ballasts 6 hrs (pp 667-730) 3 hrs 6 Design Considerations 6.1 Introduction 6.2 Snubber circuit design 6.2 Gate drive circuits 6.3 Heatsink design EE8410 3 Power Electronics Project Schedule Projects Topics Week # Project 1 DC/DC Switch Mode Power Supply 3-6 Project 2 Phase Controlled Rectifier 7-9 Project 3 Three-phase AC Power Supply 10-12 • Course grade A final letter grade shall be assigned based on the following conversion table. A+ A AB+ B B- 90% - 100% 85% - 89% 80% - 84% 75% - 79% 70% - 74% 66% - 69% C+ C CD+ D DF 63% - 65% 60% - 62% 57% - 59% 54% - 56% 52% - 53% 50% - 51% 00% - 49% Instructor David Xu, PhD Room ENG333, 245 Church Street, Toronto Department of Electrical and Computer Engineering Ryerson University (416) 979-5000 ext: 6075 eMail: [email protected] Faculty Course Survey The faculty course survey will be held in November, 2006. EE8410 4 Power Electronics 2. Design Projects 2.1 Project 1 DC/DC Switch Mode Power Supply Objectives • To review the DC/DC converters; • To become familiar with feedback control; • To study the performance of switch mode power supply; Specification • Non-isolated switch mode power supply. • Input: 48VDC • Output: 5VDC, 50W at full load. The minimum output current is 0.5A • Ripple voltage over output: ≤100mV, peak-to-peak Converter Topology Buck converter is suggested as shown in Figure 1. T1 + iL C + −E + G Vd D1 VL − − Io + L Vo − R Figure 1 Buck converter with controller Controller A voltage regulator is recommended in this project as shown in Figure 2 vo ,ref vo Figure 2 Voltage feedback control The regulators usually is lead-lag regulator (PID regulator), which widen the system bandwidth and improve the phase margin. EE8410 5 Power Electronics Requirement • A MATLAB/Simulink model is required to choose the parameters and verify the design. • Choose the proper parameters for the passive components, L and C according to the specification. Assume the passive components are ideal. • Choose the proper parameters for lead-lag regulator, assume the triangle wave is 0-10V (peak-to-peak) and the switching frequency is 50KHz, using simulation software. • Following simulation results of inductor current and output voltage waveforms at different load conditions are required in the reports. 1) Full load 2) 10% of the full load. 3) Transient procedures from 10% to 100% of the full load. 4) Transient procedures from 100% to 10% of the full load. Questions 1) In practical design, the capacitors are not ideal. How to meet the design specification? 2) How to reduce the size of your design? 3) If the supply needs to be isolated from 48V, which topology will you recommend? Why? Report Each student should develop your own simulation model and write the report. The guideline of the report is in appendix I. Submit your report with the copy of simulation model attached. EE8410 6 Power Electronics Appendix I Report Writing Guidelines Title page This page includes: the title of the report, author name, for whom and when the report was prepared. Abstract An abstract is a short paragraph summarizing the report. One or two sentences for each of the following items would be appropriate: • Purposes (objectives) • Methods • Observations (figures-of-merit) • Conclusions & recommendations An abstract can be executive summary. The reader wants to read a short paragraph and to be able to put the report into context with other relating materials without spending much time reading the whole report. Thus, an abstract requires a careful preparation and is the LAST item to be written in a report. It should be independent and the rest of the report should be written as if an abstract doesn’t exist. Introduction This paragraph explains the initiation of the study, the problem to be investigated, the approach or the method to be employed for the study. Theory Develop all theoretical formulations or explanation for the performance of the systems under investigation. If simulation is adopted, a paragraph of description should be given to the simulation models. Experiments/Simulation Results Use graphs and/or tables to show all the data. Oscilloscope tracings and/or waveform drawings should be reported in this section. Proper calculations should also be given to verify the experimental/simulation results. Conclusions & Recommendations It is important to make a precise conclusion of the project. List the major results together with short explanations and comments. Recommendations are also necessary in a report. References List all the references, such as papers, books and other reports here. Appendix, Others • Derivations of the complex equations • Simulation programs or simulation models • Others tracings or waveforms. • Materials related to the report EE8410 7 Power Electronics 2.2 Project 2 Phase Controlled Rectifier Objectives • To review the AC/DC converters; • To become familiar with feedback control of rectifier; • To study the performance of phase controlled rectifier; Specification • Isolated current source power supply. • Input: three-phase 208VAC, 60Hz. • Output: 50A at full load. • Ripple current over output: ≤1A, peak-to-peak Converter Topology Three-phase SCR rectifier is suggested as shown in Figure 3. An isolation transformer is adopted. The transformer is 10KVA, 208V/208V Y/∆ connection. The leakage inductance is 0.02pu. The load resistance is about 1Ω. v − an + v − bn + v − cn + ia T1 T3 T5 + id L ib vd ic T4 T6 T2 − Load R = 1Ω Figure 3 Three-phase SCR rectifier Controller A feedback control is recommended in this project as shown in Figure 4 id ,ref id Figure 4 Current feedback control EE8410 8 Power Electronics In this controller, a PI regulator is adopted to regulate the output current of the three-phase SCR rectifier. The current is smoothed by the dc inductor. Requirement • A MATLAB/Simulink model is required to choose the parameters and verify the design. • Choose the proper parameters for the passive component, L according to the specification. Assume L is an ideal inductor. • Choose the parameters for the PI regulator. • Following simulation results of load current and output voltage waveforms at different load conditions are required in the reports. 1) Full load at 50A, 2) Transient procedures from no load to full load. 3) Transient procedures from full load to no load. • Show the current waveforms of transformer’s primary and secondary side currents in your report. Questions 1) In practical design, the transformer is not ideal. What’s the effect of the transformer leakage inductance? 2) Which topology will you recommend to reduce the size for the current source power supply? Why? 3) How to eliminate the harmonic currents at primary side of the transformer? Report Each student should develop your own simulation model and write the report. Submit your report with the simulation models attached. EE8410 9 Power Electronics 2.3 Project 3 Three-phase AC Power Supply Objectives • To review the DC/AC converters; • To become familiar with PWM; • To study the performance of three-phase inverter; Specification • Three-phase AC power supply. • Input: 400VDC, • Output: 220VAC, rms value, 10KW at full load. The load resistance is 4.84Ω. Converter Topology Three-phase inverter is suggested as shown in Figure 5. Three-phase output LC filters are adopted to smooth the output voltage. Assume the inductance of the filter is about 0.1pu and the output filter corner frequency is 1KHz. The switching frequency is 20KHz. Figure 5 Three-phase inverter with output filter EE8410 10 Power Electronics Controller A feedback control is recommended in this project as shown in Figure 6 v A,ref vA vB ,ref vB vC ,ref vC Figure 6 AC current control In this controller, three PI regulators are adopted to regulate the output voltage. The reference voltages are three-phase sinusoidal voltages at 220V (RMS). The regulators produce the compensate voltages over the filter inductance at full load. Due to the performance of PI regulators, parameters should be carefully chosen since the reference is not DC value. The triangle waveform is ±10V peak-to-peak. Requirement • A MATLAB/Simulink model is required to choose the parameters and verify the design. • Choose the proper parameters for the passive component, L and C according to the specification. Assume L and C are ideal. • Choose the parameters for the PI regulators. Assume all the three regulators are identical. • Following simulation results of load current and output line-to-line voltage waveforms at full load conditions are required in the reports. • Show the current waveforms of collector current of IGBT T5 and inverter output current at phase A. Questions 1) How to avoid the LC resonance in the output filter. 2) How to reduce the steady state error? Which control strategy would be recommended if no steady-state error is required? 3) Analysis the relationship between inverter output voltage and load voltage at fundamental frequency, using phasor diagram. Report Each student should develop your own simulation model and write the report. Submit your report with the simulation models attached. EE8410 11 Power Electronics 3. Solutions to Selected Problems 3.1 dc-dc Switch-mode Converters Step-down Converters (Chapter 7, Moham) 7-1 VO=5V, Vd=10V to 40V, PO≥5W, fs=50kHz. Find the minimum inductance to keep the converter in the continuous conduction mode under all conditions. Solution: For a given load and output voltage, the likelihood that the inductor current will fall to zero is increased by lowering the duty ratio and thus increasing the OFF time. The duty ratio is lowest when Vd=40V. PO/VO=5W/5V=IO=1A For continuous conduction from Eq. 7 - 5, IO ≥ D [Vd − VO ] 2 fS L D= 5 D 0.125 = 0.125; L = [Vd − VO ] = [ 40 − 5] 40 2fS I O 2 × 50000 × 1 L = 43.75 µH 7-2 Vo=5V, fs=20kHz, L=0.001H, C=470µF, Vd=12.6V, Io=0.2A. Find ∆Vo. Solution: Is the circuit operating in the continuous mode? D [Vd − Vo ] = 0.0754 where D = 5 = 0.397 From Eq.7 - 5, i OB = 2 fs L 12.6 T (1 − D )Vo It is in the continuous mode, so from Eq.7 - 24 ∆Vo = s 8 LC [1 − (5 12.6)]× 5 ∆Vo = = 2.01mV 2 (20,000) × 8 × 0.001 × 470 × 10 −6 2 7-3 Find the RMS ripple current through L. (optional) Solution: iL,ripple 0.0755 A t -0.0755A DTS (1-D)TS TS EE8410 12 Power Electronics ⎡ di ⎤ V = L⎢ L ⎥ ; ⎣ dt ⎦ During t on , di L 12.6 − 5 = = 7600 A s dt 0.001 di L −5 5 = = −5000 A s ; D = = 0.397. dt 0.001 12.6 Therefore, the peak - to - peak ripple current is During t off , ∆i L = 0.397(50 µs )(7600 A s ) = 0.151A for 0 < t < 19.84 µs i L ,ripple (t ) = −0.0755 + 7600t Note : Ts = 50 µs Note : DTs = 19.84 µs for 19.84 µs < t < 50 µs = 0.1747 - 5000t T 1 s [i L ,ripple ] 2 ∂t =i L ,ripple RMS ∫ Ts 0 RMS ripple current = 43.66mA 7-5 Calculate the ripple voltage in problem 7-2 if the load current is reduced to IOB/2. (optional) Solution: Vo 5 D I o = 0.0377 A; = = ; ∴ ∆1 = 1.52 D Vd 12.6 D + ∆ 1 Using Eq.7 - 14, V T D∆ 12.6 D∆1 0.1197 I o = 0.0377 = d s 1 = ; ∴ ∆1 = , 2L 2 × 20,000 × 0.001 D 0.1197 = 1.52 D 2 ; D = 0.281. Using the equation derived in problem7 - 4, ∆VO = 1.66mV One-quadrant chopper T + G Vd iT iO L + iD R VO D Ea _ _ Fig 7-a Circuit diagram of one-quadrant chopper 7-a EE8410 In the one-quadrant chopper circuit of Fig. 7-a, Vd=600V, Ea=200V, Ts=4000µs, ton=2500µs. Show that the output current iO is continuous. Solution: 13 L=4mH, R=1.5Ω, Power Electronics τ = 4mH 1.5Ω = 2667 µs ton τ = 2500 2667 = 0.937 Ts τ = 4000 2667 = 1.5 600 e 0.937 − 1 200 Imin = − = 178.3 − 133.3 = 45A 1.5 e1.5 − 1 1.5 Since Imin > 0, iO is continuous. 7-b For the chopper circuit of problem 7-a, determine: (a) The average output voltage and current, VO and IO. (b) The output current at the instant of IGBT turn-off. Solution: (a) From Prob. 7 - a, current is continous. t VO = on V = 0.625 × 600 = 375V T V − Ea 375 - 200 IO = O = = 116.7A R 1.5 t on 2.5 × 10-3 × 1.5 = = 0. 9375 (b) τ 4 × 10-3 Ts 4 × 10-3 × 1.5 = = 1.5 τ 4 × 10-3 600 1 - e- 0.9375 200 I max = ⋅ = 179.9A 1.5 1 - e -1.5 1.5 7-c In the chopper circuit of Fig.7-a, Vd=600V, Ea=200V, L=1mH, ton=2500µs. Show that the output current iO is discontinuous. Solution: τ = 1mH 1.5Ω = 667 µs t on τ = 2500 667 = 3.748 R=1.5Ω, Ts=4000µs, and Ts τ = 4000 667 = 6.0 600 e 3.748 − 1 200 − = 41 − 133 = -92A 1.5 e 6.0 − 1 1.5 Since I min < 0, i O is discontinuous. I min = 7-d For the chopper circuit of problem 7-c, determine: (a) The average output voltage and current, VO and IO. (b) The output current at the instant of commutation. (a) Solution: τ= t on τ L 10 -3 = s R 1.5 = 2.5 × 1.5 = 3.75 10 -3 600 − 200 ln { e 3.75 [1 + (1 − e −3.75 ) ] } 1.5 200 = 3.222 × 10 -3 s tx = EE8410 14 Power Electronics VO = (b) 7-e 2 .5 (4 - 3.222) × 600 + × 200 = 413.9V 4 4 V − Ea 413.9 − 200 IO = O = = 142.6A 1 .5 R I max = 600 - 200 (1 - e-3.75 ) = 260.4A 1.5 In the chopper circuit of Fig. 7-a, Vd=600v, Ea=350V, R=0.1, Ts=1800µs, and L is of so large a value that the output current may be assumed constant or ripple-free. If the output current is to be IO=100A: (a) Calculate the required value of ton. (b) Sketch to scale the time variations of vG, vO, iO, iD and iT. Solution: VO − Ea A R VO = 0.1 × 100 + 350 = 360 V IO = (a) ton = VO = ton Vd T V 360 × 1.8 × 10− 3 = 1.08 × 10 - 3 s 600 (b) vG vO t on Ts t 600 360 t iO 100 t iD 100 t iT 100 t EE8410 15 Power Electronics 3.2 Single and Three phase Diode Rectifier 5-1 (Chapter 5, Moham) Source voltage v s (t ) = Vˆs sin ωt Differential equation (assuming that the diode is on) di Ri + L = Vˆs sin ωt dt from which V̂ di R + i = s sinωt L dt L Adding the forced response and the natural response, i = Ae R t L + V̂s sin (ωt - Φ ) Z Z = R 2 + (ωL ) , 2 where ( ) ( ) Initially at t = 0, i 0 - = i 0 + previous equation : 0 = A + ∴ A= ⎛ ωL ⎞ Φ = tan -1 ⎜ ⎟ and A is the coefficient to be determined. ⎝ R ⎠ = 0 . We will use this initial condition to calculate A in the V̂s sin (− Φ ) Z V̂s ⎛ ωL ⎞ sin Φ = Vˆs ⎜ 2 ⎟ Z ⎝Z ⎠ Vˆ ωL ∴ i(t ) = s 2 e Z R t L + Vˆs sin (ωt − Φ ) Z 5-3 v = Vd + 2V1 cos ω1t + 2V1 sin ω 1t + 2V3 cos ω 3t i = I d + 2 I 1 cos ω1t + 2 I 3 cos(ω 3t − Φ 3 ) (a ) P = Vd I d + 2V1 I 1 cos 45° + V3 I 3 cos Φ 3 (b ) V = Vd + 2 2 ( 2V1 2 I = I d + I1 + I 3 (c ) PF = P = VI ) 2 + V3 2 2 Vd I d + 2V1 I 1 cos 45° + V3 I 3 cos Φ 3 2 Vd + ( 2V 1 ) 2 2 2 2 + V3 × I d + I 1 + I 3 2 Note : 2V1 cos ω 1t + 2V1 sin ω 1t = 2V1 (cos ω 1t + sin ω 1t ) = 2 × 2V1 sin(ω 1t + 45°) = 2V1 sin(ω 1t + 45°) EE8410 where 2V1 is peak value. 16 Power Electronics 5-4 (a ) v s : Sinusoidal, Vs = 120V ∴ Vd = 0.9Vs = 108V Pd = Vd I d = 1080W (b) vs 200V 0 60° 120° vd 120° 0 180° Vd = ωt 60° 120° 60° 200V ωt (200 × 120 ) + (0 × 60 ) = 200 × 2 = 133.33V o o 3 180 o Pd = Vd I d = 1333.3W 5-6 I D (avg ) = I D (rms ) = Id 2 2 Id I = d 2 2 5-10 VS 200 ωt |VS| 200 160 ωt id 2π/3 EE8410 π 5π/3 ωt 2π 17 Power Electronics id (0) = 0 0 < ωt < ← see " hint". 2π 3 did = 200 − 160 = 40 dt di d 40 40 = = d(ωt ) ωLs 377 × 10 −3 Ls ∴ 2π ⎛ i d ⎜ ωt = 3 ⎝ ωt > 2π 3 ( ) 2π ⎞ 40 × 3 = 222.2 A = ⎟ −3 ⎠ 377 × 10 did = −160 dt di d 160 ∴ == -424.4 A rad d(ωt ) 377 × 10 -3 222.2 ∴ i d comes down to zero in = 0.523 rad ≅ 30 o 424.4 and it stays at zero until ωt = π . Ls 5-11 Calculateθ b 2Vs sinθ b = Vd ⎛ 150V ⎞ ∴ θ b = sin -1 ⎜ ⎟ = 1.084 rad. ⎝ 2 × 120V ⎠ Derive i d (θ ) i d (θ ) = 1 ωL s = 1 ωL s i d (θ ) = 1 ωL s θ ∫θ b v L dθ θ ∫θ ( ) 2Vs sin θ − Vd dθ b [ ] 2Vs (− cosθ + cosθ b ) − Vd (θ − θ b ) ∴ i d (θ ) = -450.1cosθ - 397.9θ + 641.8 Calculate θ f i d (θ f ) = 0 = -450.1cosθ f - 397.9θ f + 641.8 cosθ f + 0.884θ f = 1.426 ∴ θ f = 2.56 rad Calculate I d,peak The peak current occurs at (π - θ b ) since v L is positive between θ b and π - θ b . I d, peak = i d (π - θ b ) ; π - θ b = 2.058 rad ∴ I d,peak = -450.1cos(2.058) - (397.9 ) × (2.058) + 641.8 = 33.6A EE8410 18 Power Electronics 5-14 I s (rms ) = I d From Fourier analysis : 4 I s1 (rms ) = 2 I d = 0.9 I d π DPF angle Φ 1 = 0 2 0 I s − I s1 0 THDis = 100 2 I s1 = 100 × 1 − 0.9 2 = 48.4 0 0 0.9 DPF = 1.0 I PF = s1 DPF = 0.9 Is CF = I s,peak I s (rms ) =1 5-23 I D (avg ) = Id 120 o I = d 3 360 o I D (rms ) = Id I = d 3 3 2 5-27 i s is odd and quarter - wave symmetric. Therefore, from Table 3 - 1 a n = 0 for all n, bn = 4 π ∫ 90 o 0 b n = 0 for all even n and, i s sin (nωt )d (ωt ) for all odd n. for 0 < ωt < 30 o , is = 0 30 o < ωt < 60 0 , 4I d is = I d 30 4I d ω ω ω ( ) ( ) ( ) ∴ bn = sin = cos n t n t d t π ∫30o πn 90 o 4I = d [cos(30n )° − cos(90n )°] n = odd πn Quautity within the bracket : o 90 o 3 2 = 0 [cos(30n )° − cos(90n )°] = ∴ EE8410 bn = 4 π × 3 Id 2 3 × = Id 2 n πn for n = 1,5,7,11,13,L for all other odd n for n = 1 and 6n ± 1 where n = 1,2,3, L 19 Power Electronics From Eq. 3 - 21 ⎡ 1 ⎤ I d ⎢∑ sin (nωt )⎥ π ⎣ n ⎦ i s (t ) = 2 3 ∴ i s1 (t ) = 2 3 ∴ Φ1 = 0 π I d sin ωt for n = 1 DPF = 1.0 and (Eq. 5 - 72 ) 1 ⎛2 3 ⎞ 6 ⎜ ⎟= I d ⎟ π Id 2 ⎜⎝ π ⎠ 1 (Eq. 5 - 71) = n (Eq. 5 - 70) I s1 = I sn I s1 I s = I s1 + ∑ I sn 2 2 2 2 ⎛ 6 ⎞ ⎡ 1⎞ ⎤ ⎛ I d ⎟⎟ ⎢1 + ∑ ⎜ ⎟ ⎥ = ⎜⎜ ⎝ π ⎠ ⎢⎣ n =5 ⎝ n ⎠ ⎦⎥ = 6 π PF = DPF EE8410 1 = 0.816I d 2 n =5 n Id 1+ ∑ I s1 = 0.955 Is (Eq. 5 - 69) (Eq. 5 - 73) 20 Power Electronics 3.3 Single and Three Phase Thyristor Rectifiers 6-3 (Chapter 6, Moham) vs Vm π ωt 2π Vm vd A1 Vm α π+α π T1 and T2 on v d = Vm − A1 π T3 and T4 on ( ) = Vm − 2α Vm ( 2α π = Vm 1 − π At α = 45°, v d = 100V ωt 2π ) At α = 135°, v d = −100V 6-5 (a ) Vdo = 0.9 Vs π 2 Vs α π Vdα = 2 Vs ∫ sin ωt d(ωt ) π = DPF = cos(α 2) [cosα + 1] 180° - α 180° can be calculated by equating power : Vs I s1 ⋅ DPF = Vdα I d Is = Id I s1 I s1 = (b ) 1 Vdα = Vdo 2 2 ⋅ Vs (1 + cosα ) = 1 × 0.9 ⋅ Vs π 2 π × 0.9 −L cosα = 2 2 α = 90° ∴ or ∴ ∴ EE8410 Vdα I d Vs cos(α 2 ) ∴ DPF = cos(α 2 ) = 0.707 21 Power Electronics 180 − 90 = 0.707 I d 180 0.5 × 0.9Vs I s1 = I d = 0.636 I d Vs cos(90° 2 ) Is = Id ∴ PF = I s1 ⋅ DPF = 0.636 Is 2 THDi = (c ) I s − I s1 (d ) 6-6 6-7 %= I s1 0.707 2 − 0.636 2 % = 48.55% 0.636 In a full - bridge converter, (Eq. 6 - 6) Vdα = Vdo cos α ∴ 2 α = 60° for Vdα = 0.9Vo , DPF = cos α = 0.5 (Eq. 6 - 16 ) PF = 0.9 cos α = 0.45 (Eq. 6 - 17 ) THDi = 48.43% Comparision of (b) and (c) shows that the Power Factor is better in the half - controlled converter I thy (avg ) 1 I thy (rms ) 1 = , = Id Id 2 2 Pd = 1 KW , I d = 10 A, i d ≅ I d , Vs = 115V (+ 5%, - 10% ) Calculate L s : ω = 2π × 60 = 377 rad s Transformer VA = 1500VA rated Vpri = 120V , rated I pri = 1500 Z base = V pri I pri 120 = 12.5 A (rated ) = 9.6Ω ωLs = (8% ) Z base or L s = 0.08 × 9.6 377 ≅ 2mH α cannot go below 0! Therefore, to calculate the minimum transformer turns ratio a (where a = V pri Vsec ), 0.9 2 Vs cos α − ω (Ls )I d π a Substitute Vd = 100V , α = 0° and Vs, min = 115V (− 10% ) = 103.5V in Eq. 6 - 26, Vd = ∴ From the above equation, a min = 0.89 With a min and Vs = 115V (+ 5% ) = 120.75V , the above equation yields α = 31° for Vd = 100V . EE8410 22 Power Electronics 6-11 3ωLs Vd = Vdo cos α − π cos(α + u ) = cos α − Vdo = 3 2 π (Eq. 6 - 55) Id 2ωLs 2VLL I d (Eq. 6 - 62) (Eq. 6 - 36) VLL Replacing (ωL s I d ) in Eq. 6 - 55 by Eq. 6 - 62, 3 2 V V [cos α − cos(α + u )] = Vdo cos α − do [cos α − cos(α + u )] 2 π 2 LL ∴ Vd = Vdo cos α − ∴ Vd = ∴ Vdo 2 [cosα + cos(α + u )] Vdo I d [cos α + cos(α + u )] 2 On the ac side, ac power is Pac = 3V LL I s1 cos φ1 dc power Pd = Vd I d = Approximation : I s1 ≅ 6 π Id (Eq. 6 - 44) The above equation is approximate because the above equation is correct only if L s = 0 (and hence u = o). ∴ Pac ≅ 3VLL 6 π I d cos φ1 Equating Pac = Pdc 3V LL ∴ 6 π I d cos φ1 ≅ DPF = cos φ1 ≅ 3 2 π V LL Id [cosα + cos(α + u )] 2 1 [cosα + cos(α + u )] 2 6-12 VLL = 460V , f = 60Hz, ω = 377 rad , L s = 25µH , Vd = 525V , and Pd = 500kW . s Pd 500 × 1000 = = 952.4 A Id = 525 Vd Vd = 1.35V LL cos α − 3ωL π Id ⎛ 3 × 377 ⎞ 525 + ⎜ × 25 × 10 −6 × 952.4 ⎟ π ⎝ ⎠ ∴ cos α = 1.35 × 460 ∴ α = 30.77° cos(α + u ) = cos α − 2ωLs 2V LL I d = 0.859 − 2 × 377 × 25 × 10 −6 2 × 460 × 952.4 = 0.831 or (α + u ) = 33.76° Therefore, the commutation angle u is u = 33.76° - 30.77° ≅ 3° EE8410 23 Power Electronics 6-a EE8410 Consider the 3φ full bridge thyristor rectifier shown in Fig.6-19 (page 138). Draw waveforms of VPn , VNn and Vd at α=30°, 90° and 150°. 24 Power Electronics 3.4 Switch Mode Inverters 8-a (Chapter 8, Moham) The single-phase half-bridge inverter in Fig.8-4 has a resistive load of R=2.4Ω and the dc input voltage is Vd=48V. Consider square wave operation with device conduction angle of 180° per cycle. Determine (a) the rms output voltage Vo1 at the fundamental frequency; (b) the average output power Po; (c) the peak and average currents of each transistor; and (d) the total voltage harmonic distortion. Solution: (a ) Fourier series vo = ∞ 2Vd sin( nωt ) n=1, 3, 5L nπ ∑ Vo1 = 0.45 × 48 = 21.6 V (b) Po = (c ) 1 T 2 vo dt = 24 V T ∫0 Vo = Vo2 I Peak = R Vd = 240 W = 10 A 2R Duty cycle = 50% I avg = 0.5 ×10 = 5 A Vo2 − Vo21 = Vo1 (d ) THD = 8-b 24 2 − 21.6 2 = 0.48 21.6 Repeat Problem 8-a for a single phase bridge inverter in Fig.8-11. Solution: (a) Fourier series vo = ∞ 4Vd sin(nωt ) n =1, 3, 5L nπ ∑ Vo1 = 0.9 × 48 = 43.2 V (b) Po = (c ) EE8410 Vo2 I Peak = Iavg (d ) 1 T 2 vo dt = 48 V T ∫0 Vo = R Vd = 960W = 20 A R = 0.5 × 20 = 10 A Vo2 − Vo21 THD = = 0.48 Vo1 25 Power Electronics 8-c The single phase full bridge inverter in Fig.8-11 has an RLC load with R=10Ω, L=31.5mH, and C=112µF. The inverter frequency fo = 60Hz and dc input voltage Vd = 220V. Consider the square wave operation with device conduction angle of 180° per cycle. (a) Express the instantaneous load current in Fourier series; (b) Calculate the rms load current I1 at the fundamental frequency; (c) Calculate the THD of the load current; (d) Calculate the power absorbed by the load Po and the fundamental power Po1; and (e) Calculate the average current of dc supply Id. Solution: The inductive reactance for the nth harmonic voltage is X L = j 2nπ × 60 × 31.5 × 10 −3 = j11.87n Ω The capacitive reactance for the nth harmonic voltage is j10 6 − j 23.68 = Ω 2nπ × 60 × 112 n The impedance for the nth harmonic voltage is XC = − [ Z n = 10 2 + (11.87n − 23.68 n) ] 2 12 and the power factor angle for the nth harmonic voltage is θ n = tan −1 (a ) 11.87n − 23.68 n 2.368 ⎞ ⎛ = tan −1 ⎜1.187n − ⎟ n ⎠ 10 ⎝ The instantaneous output voltage can be expressed as v o (t ) = 280.1sin(337t ) + 93.4 sin(3 × 377t ) + 56.02 sin(5 × 337t ) + 40.02sin(7 × 377t ) + 31.12 sin(9 × 377t ) + L Dividing the output voltage by the load impedance and considering the appropriate delay due to the power factor angles, we can obtain the instantaneous load current as ( ) ( ) + sin(5 × 377t - 79.63 ) + 0.5 sin(7 × 377t − 82.85 ) + 0.3sin(9 × 377t - 84.52 ) + L i o (t ) = 18.1sin 377t + 49.72o + 3.17 sin 3 × 377t − 70.17 o o o o (b) I o1 = 18.1 2 = 12.8 A (c) Consider up to the ninth harmonic. I o = I o21 + I o23 + L + I o29 = 13.02 THD = (d) I o2 _ I o21 I o1 = 18% Po = I o2 R = 1695 W Po1 = I o21 R = 1638.4 W (e) EE8410 I d = Po Vd = 7.7 A 26 Power Electronics Repeat Problem 8-c assuming that C = 0. 8-d The solution to this problem is not provided. 8-e In the single phase full bridge PWM inverter circuit of Fig.8-11, Vd = 300V, ma =0.8, mf = 39 and the frequency of the sine modulating wave is 60Hz. The load resistance is 10Ω and load inductance is 1mH. Bipolar modulation technique is used. Determine (a) switching frequency of each transistor; (b) the rms values of voltage and current at the fundamental frequency; (c) the rms values of 37th and 39th harmonic voltages and currents; and (d) the ratio of 39th harmonic current to fundamental current. Answers: (a) f sw = 60 Hz × 39 = 2340 Hz (b) From Table 8 - 1, the rms voltage of fundamental is 0.8Vd V 169.7 Vo1 = = 169.7V I o1 = o1 = = 16.96 A ZL1 10 + j 2 × π × 60 × 0.001 2 (c ) Vo37 = 0.22Vd = 46.67V 2 Vo39 = 0.818Vd = 173.52V 2 (d ) I o37 = Vo37 46.67 = = 2.719 A ZL37 10 + j 2 × 37 × π × 60 × 0.001 I o39 = Vo39 173.52 = = 9.759 A ZL39 10 + j 2 × 39 × π × 60 × 0.001 I o39 Io1 = 0.575 8-f Consider a 3Φ inverter in Fig.8-21. Assume that IGBTs are used as switching devices. The conduction angle of each IGBT is 180o per cycle. (a) Draw waveforms of IGBT gate signals, line-to-line and line-to-neutral voltages of the inverter. (b) Derive an expression for the calculation of rms values of line-to-line and line-to-neutral voltages. (c) Derive an expression for the calculation of rms values of fundamental components of lineto-line and line-to-neutral voltages. 8-g The three-phase inverter in Fig.8-21 has a wye-connected load of R = 5Ω and L = 23mH. The inverter frequency is fo= 60Hz and the dc input voltage is Vd = 220V. The conduction angle of each switching device is 1800 per cycle. (a) Express the instantaneous line-to-line voltage vab(t) and line current ia(t) in a Fourier series. (b) Determine the rms line voltage VL ; (c) Calculate the rms phase voltage VP; (d) Calculate the rms line voltage VL1 at the fundamental frequency; (e) Calculate the rms phase voltage at the fundamental frequency, VP1; (f) Determine the total harmonic distortion THD of line current ia; (g) Determine the load power Po; and (h) Determine the average dc current Id. Solution (continued on next page): EE8410 27 Power Electronics (a ) Refer to your class notes. The instantaneous line - to - line voltage v ab (t ) can be written as v ab (t ) = 242.58 sin (337t + 30°) − 48.52 sin 5 × (377t + 30°) − 34.66 sin 7 × (377t + 30 o ) + 22.05sin 11 × (337t + 30 o ) + 18.66 sin 13 × (377t + 30 o ) − 14.27 sin 17 × (377t + 30o ) + L Z L = R 2 + (nωL ) ∠ tan −1 (nωL R ) = 5 2 + (8.67 n ) ∠ tan −1 (8.67 n 5) 2 2 i a (t ) = 14 sin(377t − 60 o ) − 0.64 sin(5 × 377t − 83.4 o ) − 0.33 sin(7 × 377t − 85.3o ) + 0.13 sin(11 × 377t − 87 o ) + 0.10 sin(13 × 377t − 87.5o ) − 0.06 sin(17 × 377t − 88o ) − L (b) VL = 0.8165 × 220 = 179.63 V . (c) Vp = 0.4714 × 220 = 103.7 V . (d ) VL1 = 0.7797 × 220 = 171.53 V . (e) Vp1 = VL1 (f) = 99.03 V . 3 Consider up to 17th harmonic. (0.64 THD = ) 1 + 0.332 + 0.132 + 0.10 2 + 0.06 2 2 = 0.053 14 ( g ) For wye - connected loads, the line current is the same as the phase current. The rms line current is (14 = 2 ) 1 + 0.64 2 + 0.332 + 0.132 + 0.10 2 + 0.06 2 2 IL = 9.91 A 2 The load power Po = 3I L2 R = 3 × 9.912 × 5 = 1473 W . 2 (h) The average dc current I d = Po 220 = 1473 220 = 6.7 A. 8-h The three phase inverter in Fig.8-21 operates in a PWM mode. A three phase wye-connected load of R = 10Ω and L = 2mH is connected to the inverter. The input dc voltage is 240V. The gating pattern is sinusoidally modulated with ma = 1.0 and mf = 21. The fundamental frequency is 100Hz. Determine: (a) the rms values of fundamental voltage and current; (b) the rms values of 5th and 7th harmonic voltages and currents; and (c) the rms values of 19th and 23rd harmonic voltages and currents. The solution to this problem is not provided. EE8410 28 Power Electronics 4. Examination Samples MIDTERM EXAMINATION ELE 754 Power Electronics Ryerson University Department of Electrical and Computer Engineering Duration: 2 hours Instructor: Dr. B.Wu Instructions: 1. Answer all four questions. 2. Show details of your derivations/calculations. Marks: Q1. 30% ______________ Q2. 20% ______________ Q3. 30% ______________ Q4. 20% ______________ Student Name: _________________________________ Student Number: _________________________________ Question 1 (30%) EE8410 29 Power Electronics iT T + iO + iD G R D Vd Vo Ea - - Fig. 1 One quadrant chopper with a dc motor load An IGBT-based one quadrant chopper is used to drive a dc motor, whose armature circuit parameters are represented by the winding resistance R (0.2 Ohms), winding inductance L (0.25mH) and back emf as shown in Fig.1. The input dc voltage of the chopper is 115V and its switching frequency is 500Hz. When the duty cycle of the chopper is 0.4, the motor runs at 1200rpm with its emf of 55V. Answer Questions 1.1 to 1.3. 1.1) The peak value of armature current. 3% 1.2) L 0.25 × 10 −3 = = 1.25 × 10 −3 , 0.2 R V − Ea (1 − e −ton / τ ) I o, peak = d R 115 − 55 = (1 − e − 0.64 ) = 141.8 A 0 .2 τ= t on = 0.4 × t on / τ = 0.64 Ts τ 115 e0.64 − 1 55 × − = −144.6 A 0.2 e1.6 − 1 0.2 I o ,min = 3% ⎧ ⎡ 115 − 55 t x = 1.25 × 10 −3 ln ⎨e 0.64 ⎢1 + 1 − e −0.64 55 ⎣ ⎩ 2ms = 1 .6 1.25ms ← discontinuous mode ( = 1.25 × 10 −3 ln(2.874) = 1.32ms 0 .8 2 − 1.32 Vo ,dc = 115 × + 55 = 64.7V 2 2 EE8410 = The average (dc) armature voltage and armature (dc) current. 3% 1.3) 1 = 0.8 × 10 −3 sec 500 )⎤⎥ ⎫⎬ ⎦⎭ I o, dc = 64.7 − 55 = 48.5 A 0 .2 Sketch to scale the waveforms of vo and io, indicating the peak values. 30 Power Electronics 3% Vo 115V tx iO 141.8V Question 1 (continued) An external dc choke of 6mH is connected in series with the armature winding of the above mentioned dc motor. The duty cycle is adjusted to 0.5 and the motor runs at 1120rpm. The field winding current remains unchanged. Find: 1.4) The dc component (average value), fundamental component (peak value) and third harmonic (pick value) in. 3% Vo,dc = ________ 3% Vo1, peak = ________ 3% Vo3, peak = ________ Check: continuous or discontinuous mode? L 6.25 × 10 −3 = = 31.25 × 10 −3 , 0.2 R 1 .0 t on / τ = = 0.032 31.25 τ= I o ,min = t on = 0.5 × 2ms = 1.0ms Ts τ = 2ms = 0.064 31.25ms 115 e 0.032 − 1 51.33 × − = 26.25 A ← continuous mode 20 e 0.064 − 1 0.2 Ea = 55 × 1120 = 51.33 1200 Vo Vd Use Fourier Series to find Vo,dc, Vo1, peak and V03, peak EE8410 31 Power Electronics 1.5) The dc component (average value), fundamental component (peak value) and third harmonic (peak value) in io. = ________ 3% Io,dc 3% Io1, peak = ________ 3% Io3, peak = ________ Vo 115V π Vo = 115 + 2 ωt 2π 10 ∑ n = 1 , 3 , 5 ... 4 × 57 . 5 sin( n ω t ) nπ = 57.5 + 73.21sin ωt + 24.4 sin 3ωt + 14.64 sin 5ωt + ... ↑dc I o, dc = I o1, peak ↑1st ↑3rd 57.5 − 51.33 = 30.82 A 0.2 73.21V 73.2 = 3.73 A = = R 2 + ωL2 0.2 2 + (2π × 500 × 6.25 ×10 −3 ) 2 I o3, peak = 24.4 0.2 + (2π × 3 × 500 × 6.25 ×10 −3 ) 2 2 = 0.414 A Question 2 (20%) The input terminals of a single phase full bridge diode rectifier are connected to a single phase ac voltage source rated at 208V and 400Hz with a source inductance of 4%. The rectifier is rated at 20kVA. The load of this rectifier is an ideal dc voltage source of 240V. Answer the following questions: 2.1) 4% Find the value of source inductance in mH. 2.2) 4% Derive an expression for the calculation of output dc current. EE8410 32 Power Electronics 2.3) 6% Sketch to scale the waveforms of input voltage, dc voltage, dc current, and the voltage on source inductance. 2.4) Calculate the diode conduction angle per half cycle of the input line frequency. 6% Solutions: 2.1) vs 15000 I rated = = 72.12 A 294V 208 208 Z rated = = 2.884Ω θb θp 72.12 id 383.2A 2.884 Lrated = = 1.148mH use equ (1) 2π × 400 θf L = 0.04 × 1.148 = 45.9 × 10 − 6 H vL 294V - 240V = 54V 2.2) θ b = sin −1 240 = 54.67° = 0.945rad 2 × 208 θ p = π − θ b = 2.187rad [ 1 2 × 208(− cos θ + cos 0.954 ) − 240(θ − 0.954) 2π × 400 × 45.9 × 10 −6 id = 8.668(−294.1 cos θ + 170.1 − 240θ + 228.96) id = ] id = −2549 cos θ − 2080θ + 3459 A......................equ (1) 2.4) θf = ? − 2549 cosθ f − 2080θ f + 3459 = 0 cosθ f + 0.816θ f = 1.357 Try θf = 2.6 Try θf = 2.8 Try θf = 2.82 cosθ + 0.816θ = 1.265 cosθ + 0.816θ = 1.342 cosθ + 0.816θ = 1.352 conduction angle: θf - θ = 2.82 – 0.954 = 1.866 rad = 106.9° EE8410 33 Power Electronics Question 3 (30%) A three-phase full bridge SCR rectifier without a freewheeling diode is connected to a three phase balanced voltage source of 60Hz, 208V (line to line). Assume the load of the rectifier is a constant current source of 100A and its firing (daley) angle is 60 degrees. Find: 3.1) The average dc output voltage of the rectifier. 6% Vd = 1.35 × 208 × cos α = 140.4V at which α is 60° 3.2 12% The total harmonic distortion of the input current and overall input power factor. Ia = 1 2π 2π ∫i a 2 dωt = 0.816 I d = 81.6 A 0 ia = 1.1I d sin(ωt − α ) − 0.22 I sin 5(ωt − α ) + ... THD = 1.1I d = 77.78 A 2 1 DF = = 0.995 , 1 + THD 2 PF = DF × DPF = 0.478 I a1 = 3.3 6% 2 I a − I a1 I a1 2 2 = 31% DPF = cos α = 0.5 Use Fig.2 given below, draw the dc output waveform assuming that the delay angle remains at 60 degrees. α α EE8410 34 Power Electronics 3.4 If a freewheeling diode is connected in parallel with the dc current source, draw the dc output waveform assuming that the delay angle remains at 90 degrees 6% α α Question 4 (20%) 4.1) List four switching devices that are commonly used in power electronic converters. IGBT, GTO, MOSFET, SCR 4.2) Indicate which of the switching devices you have listed are voltage controlled devices and which are current controlled devices. IGBT, MOSFET →Voltage Controlled Devices SCR, GTO → Current Controlled Devices 4.3) Draw a typical circuit diagram of an IGBT-based two quadrant chopper. + Vd LOAD - 4.4) Draw a curve which illustrates the relationship between the boundary current and the duty cycle D of a buck converter. IBD D 4.5) Write an equation which describes a dynamic relationship between motor speed, electromagnetic dω m J = Te − TL − Bω m torque and load torque. dt In the following multiple-choice questions, circuit one best answer. 4.6) EE8410 In a single phase, single diode rectifier with an RL load, the diode conduction angle is a) grater than 180°. b) less than 180°. c) equal to 180°. d) grater than 120°. e) less than 120°. f) equal to 120°. g) grater than 60°. h) less than 60°. i) equal to 60°. j) none of the above. 35 Power Electronics 4.7) In a three-phase, full SCR bridge rectifier with a three RL load where L is assumed very large, the delay angel is 60 degrees. The SCR conduction angle is a) grater than 180°. b) less than 180°. c) equal to 180°. d) grater than 120°. e) less than 120°. f) equal to 120°. g) grater than 60°. h) less than 60°. i) equal to 60°. j) none of the above. 4.8) In a three-phase, full SCR bridge rectifier with SCR conduction angle is a) grater than 180°. b) less than 180°. d) grater than 120°. e) less than 120°. g) grater than 60°. h) less than 60°. 4.9) a three R load, the delay angel is 60 degrees. The c) equal to 180°. f) equal to 120°. i) equal to 60°. j) none of the above. The maximum voltage and current ratings of a single IGBT device currently available in the market are a) 600A, 1000V b) 600A, 2000V c) 600A, 4500V d) 600A, 6500V e) 1200A, 1000V f) 1200A, 2000V g) 1200A, 4500V h) 1200A, 6500V 4.10) The source inductance between an ideal voltage source and three phase SCR rectifier a) may be used to assist SCR commutation b) may increase input current THD c) may reduce the dc output voltage d) may increase the dc output voltage d) none of the above. EE8410 36 Power Electronics