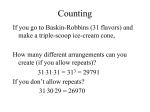Download Section 4 - The University of Kansas

Section 4.2 The Pigeonhole Principle
Pigeonhole principle:
Example 1: In any set of five numbers, there are two numbers x
and y such that x  y (mod 4).
Example 2: If five numbers are chosen from the set {1, 2, 3, 4, 5,
6, 7, 8}, then two of the numbers chosen must have a sum of 9.
The generalized pigeonhole principle:
Example 3:
Example 4:
Example 5:
More Examples
Example 6: Given a group of six acquaintances prove there are 3
mutual friends or 3 mutual enemies.
Example 7: How many students each of whom come from one of
the 50 states must be enrolled at a university to guarantee there
are at least 100 who come from the same state?
Example 8: How many people must be in a room to guarantee
that two people have the same first and last initials?
Section 4.3 Permutations and Combinations
Let alphabet  = {a, b, c, d, e}.
A permutation of a set of distinct objects is
An r-permutation is
Notation: P(n, r)
Example:
Theorem: The number of r permutations of a set with n distinct
elements, n ≥ r is
P(n, r) =
Corollary: P(n, n) = n!/0! = n!/1 = n!
Combinations
An r-combination is
Notation: C(n, r) or
Combinatorial Identities
C(n, r) = C(n, n-r)
n
Σ C(n, i) = 2n
i=0
Examples
Example 1: How many ways are there to choose a five card poker
hand?
Example 2: A committee is chosen from a group of 4 men and 6
women.
a) In how many ways can a committee of size three be chosen?
b) In how many ways can a committee of size three be chosen if
there must be 1 man and 2 women?
Example 3: How many five card poker hands contain at least one
ace?
Why won’t the following approach work?
More examples
Example 4: How many seven card poker hands contain
a. 3 spades and 4 red cards
b. 3 cards of one rank and two cards each of two other ranks
c. 3 cards each of two ranks
d. all red cards with two cards each of three ranks
e. exactly one queen and exactly four spades
Example 5: How many ternary strings of length 10 are there with
a. exactly two 0’s, three 1’s and five 2’s
b. exactly two 0’s, three 1’s and five 2’s with each 1 immediately
preceded by a 2.
Example 6: You invite nine friends to join you at dinner. How
many ways can the ten of you be seated around a circular table?
Section 4.4 Binomial Coefficients
Binomial Theorem
(a + b)0 = 1
(a + b)1 = a + b
(a + b)2 =
(a + b)3 =
The binomial theorem:
(a + b)n = C(n, 0)an + C(n, 1)an-1b + C(n, 2) an-2b2 + …
+ C(n, n-1)abn-1 + C(n, n)bn
Pascal’s Identity: C(n, k) = C(n-1, k) + C(n-1, k-1).
Combinatorial Proof of the identity
There are two ways to get a subset of S of size k
1:
2:
More on Binomial Coefficients
Example: find the coefficient of x5y4 in the expansion of (x + y)9
p. 333 #7 Find the coefficient of x9 in the expansion of (2 - x)19.
p. 333 # 23 Show C(n+1, k) = (n+1)•C(n, k-1)/k
Section 4.5 Generalized Permutations and Combinations
How many arrangements are there of the letters in the word
TOPEKA?
How many arrangements are there of the letters in the word
Kansas?
Combinations with Repeated Elements
Counting Methods to try
To count the number of …
Subsets of n-element set
e.g. number of distinct subsets
from the letters in {a, b, c, d, e}
Outcomes of successive events
e.g. number of ways to award 1st,
2nd and 3rd prizes
Outcomes of disjoint events
e.g. ways to pick either a dog or a
cat from a pet store
Outcomes given specific choices at
each step
e.g. number of ways a best 3 of 5
series can be played
Elements in nondisjoint sets
e.g. pick a spade or a queen from a
deck of cards
Ordered arrangements of r objects out
of n distinct objects
e.g. number of 5 letter words from
{a,…z} without repetition
Ordered arrangements of r objects out
of n distinct objects, repetition allowed
e.g. strings of length 6 from the
set {a,b,c,d}
Ways to choose r out of n distinct
objects
e.g. committee of size five from a
group of size 20
Ways to choose r out of n distinct
objects with repetition allowed
e.g. choose 6 pieces of fruit from
baskets of apples and pears
Method to try
Use formula 2n
Multiply number of outcomes for
each event
Add number of outcomes for each
event
Use a decision tree
Use inclusion exclusion
Use P(n, r) formula
Use nr formula
Use C(n, r) formula
Use C(r + n - 1, r) formula
Modification of Table 3.2 in Gersting