Download Confidence Intervals for Means

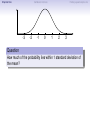
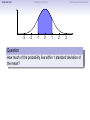
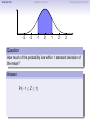
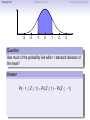
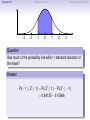
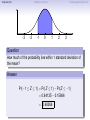
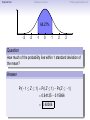
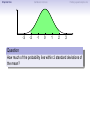
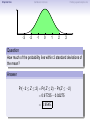
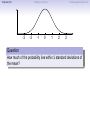
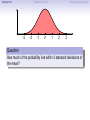
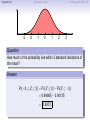
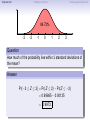
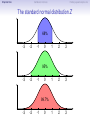
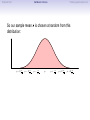
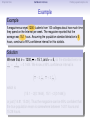
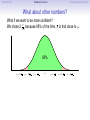
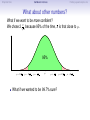
Empirical Rule
Confidence Intervals
Outline
1
Empirical Rule
2
Confidence Intervals
3
Finding a good sample size
Finding a good sample size
Empirical Rule
Confidence Intervals
Outline
1
Empirical Rule
2
Confidence Intervals
3
Finding a good sample size
Finding a good sample size
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 1 standard deviation of
the mean?
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 1 standard deviation of
the mean?
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 1 standard deviation of
the mean?
Answer
Pr(−1 ≤ Z ≤ 1)
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 1 standard deviation of
the mean?
Answer
Pr(−1 ≤ Z ≤ 1) = Pr(Z ≤ 1) − Pr(Z ≤ −1)
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 1 standard deviation of
the mean?
Answer
Pr(−1 ≤ Z ≤ 1) = Pr(Z ≤ 1) − Pr(Z ≤ −1)
= 0.84135 − 0.15866
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 1 standard deviation of
the mean?
Answer
Pr(−1 ≤ Z ≤ 1) = Pr(Z ≤ 1) − Pr(Z ≤ −1)
= 0.84135 − 0.15866
= 0.68269.
Empirical Rule
Confidence Intervals
Finding a good sample size
68.27%
-3
-2
-1
0
1
2
3
Question
How much of the probability lies within 1 standard deviation of
the mean?
Answer
Pr(−1 ≤ Z ≤ 1) = Pr(Z ≤ 1) − Pr(Z ≤ −1)
= 0.84135 − 0.15866
= 0.68269.
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 2 standard deviations of
the mean?
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 2 standard deviations of
the mean?
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 2 standard deviations of
the mean?
Answer
Pr(−2 ≤ Z ≤ 2) = Pr(Z ≤ 2) − Pr(Z ≤ −2)
= 0.97725 − 0.02275
= 0.9545.
Empirical Rule
Confidence Intervals
Finding a good sample size
95.45%
-3
-2
-1
0
1
2
3
Question
How much of the probability lies within 2 standard deviations of
the mean?
Answer
Pr(−2 ≤ Z ≤ 2) = Pr(Z ≤ 2) − Pr(Z ≤ −2)
= 0.97725 − 0.02275
= 0.9545.
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 3 standard deviations of
the mean?
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 3 standard deviations of
the mean?
Empirical Rule
Confidence Intervals
-3
-2
-1
0
Finding a good sample size
1
2
3
Question
How much of the probability lies within 3 standard deviations of
the mean?
Answer
Pr(−3 ≤ Z ≤ 3) = Pr(Z ≤ 3) − Pr(Z ≤ −3)
= 0.99865 − 0.00135
= 0.9973.
Empirical Rule
Confidence Intervals
Finding a good sample size
99.73%
-3
-2
-1
0
1
2
3
Question
How much of the probability lies within 3 standard deviations of
the mean?
Answer
Pr(−3 ≤ Z ≤ 3) = Pr(Z ≤ 3) − Pr(Z ≤ −3)
= 0.99865 − 0.00135
= 0.9973.
Empirical Rule
Confidence Intervals
Finding a good sample size
The standard normal distribution Z
68%
-3
-2
-1
0
1
2
3
1
2
3
1
2
3
95%
-3
-2
-1
0
99.7%
-3
-2
-1
0
Empirical Rule
Confidence Intervals
Finding a good sample size
Any normal distribution X
68%
µ − 3σ µ − 2σ µ − σ
µ
µ + σ µ + 2σ µ + 3σ
95%
µ − 3σ µ − 2σ µ − σ
µ
µ + σ µ + 2σ µ + 3σ
99.7%
µ − 3σ µ − 2σ µ − σ
µ
µ + σ µ + 2σ µ + 3σ
Empirical Rule
Confidence Intervals
Finding a good sample size
Empirical Rule
If X is a normal random variable with standard deviation σ,
68% of the probability is within σ of the mean.
95% of the probability is within 2σ of the mean.
99.7% of the probability is within 3σ of the mean.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example Problem
We now can get approximate answers to some problems
without the z-table!
Example
The heights of men aged 20 to 29 are approximately normal
with mean 6900 and standard deviation 2.800 .
1
About what percentage of these men measure between
6600 and 7200 ?
2
Find a range of heights that contains 95% of these men.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example Problem
We now can get approximate answers to some problems
without the z-table!
Example
The heights of men aged 20 to 29 are approximately normal
with mean 6900 and standard deviation 2.800 .
1
About what percentage of these men measure between
6600 and 7200 ?
2
Find a range of heights that contains 95% of these men.
Solution
1
µ = 69 and σ = 2.8, so 6600 is about one standard
deviation below the mean and 7200 is about one standard
deviation above the mean. Thus, by the Empirical Rule, a
little more than 68% of the men fall within that range.
(Exact answer: 71.5%)
Empirical Rule
Confidence Intervals
Finding a good sample size
Example Problem
We now can get approximate answers to some problems
without the z-table!
Example
The heights of men aged 20 to 29 are approximately normal
with mean 6900 and standard deviation 2.800 .
1
About what percentage of these men measure between
6600 and 7200 ?
2
Find a range of heights that contains 95% of these men.
Solution
1
µ = 69 and σ = 2.8, so 6600 is about one standard
deviation below the mean and 7200 is about one standard
deviation above the mean. Thus, by the Empirical Rule, a
little more than 68% of the men fall within that range.
(Exact answer: 71.5%)
Empirical Rule
Confidence Intervals
Finding a good sample size
Example Problem
Example
The heights of men aged 20 to 29 are approximately normal
with mean 6900 and standard deviation 2.800 .
1
About what percentage of these men measure between
6600 and 7200 ?
2
Find a range of heights that contains 95% of these men.
Solution, cont.
2
By the Empirical Rule, 95% of the men fall within the range
from µ − 2σ to µ + 2σ. Thus the range from
69 − 2 · 2.8 = 63.4
to
69 + 2 · 2.8 = 74.6
contains 95% of the men, so our answer is “63.4 to 74.6
inches.” (More exact answer: 63.51 to 74.49 inches.)
Empirical Rule
Confidence Intervals
Finding a good sample size
Example Problem
Example
The heights of men aged 20 to 29 are approximately normal
with mean 6900 and standard deviation 2.800 .
1
About what percentage of these men measure between
6600 and 7200 ?
2
Find a range of heights that contains 95% of these men.
Solution, cont.
2
By the Empirical Rule, 95% of the men fall within the range
from µ − 2σ to µ + 2σ. Thus the range from
69 − 2 · 2.8 = 63.4
to
69 + 2 · 2.8 = 74.6
contains 95% of the men, so our answer is “63.4 to 74.6
inches.” (More exact answer: 63.51 to 74.49 inches.)
Empirical Rule
Confidence Intervals
Finding a good sample size
Example Problem
Example
The heights of men aged 20 to 29 are approximately normal
with mean 6900 and standard deviation 2.800 .
1
About what percentage of these men measure between
6600 and 7200 ?
2
Find a range of heights that contains 95% of these men.
Solution, cont.
2
By the Empirical Rule, 95% of the men fall within the range
from µ − 2σ to µ + 2σ. Thus the range from
69 − 2 · 2.8 = 63.4
to
69 + 2 · 2.8 = 74.6
contains 95% of the men, so our answer is “63.4 to 74.6
inches.” (More exact answer: 63.51 to 74.49 inches.)
Empirical Rule
Confidence Intervals
Outline
1
Empirical Rule
2
Confidence Intervals
3
Finding a good sample size
Finding a good sample size
Empirical Rule
Confidence Intervals
Finding a good sample size
How good is a sample mean x?
Say we have a population and we want to know its mean µ.
So we choose a sample, measure it, and compute the
sample mean x.
Of course x could be larger or smaller than µ.
How likely is it to be close to µ?
Empirical Rule
Confidence Intervals
Finding a good sample size
Recall the Central Limit Theorem
Population Distribution
Mean µ
Standard deviation σ
µ
Central Limit Theorem
X is normally distributed
with mean µ,
and with standard deviation
√σ .
n
Empirical Rule
Confidence Intervals
Finding a good sample size
Recall the Central Limit Theorem
Population Distribution
Mean µ
Standard deviation σ
µ
Distribution of X
Mean µ
Standard deviation
σ
√
n
µ
Central Limit Theorem
X is normally distributed
with mean µ,
and with standard deviation
√σ .
n
Empirical Rule
Confidence Intervals
Finding a good sample size
Recall the Central Limit Theorem
Population Distribution
Mean µ
Standard deviation σ
µ
Distribution of X
Mean µ
Standard deviation
σ
√
n
µ
Central Limit Theorem
X is normally distributed
with mean µ,
and with standard deviation
√σ .
n
Empirical Rule
Confidence Intervals
Finding a good sample size
Recall the Central Limit Theorem
Population Distribution
Mean µ
Standard deviation σ
µ
Distribution of X
Mean µ
Standard deviation
σ
√
n
µ−
σ
√
n
Central Limit Theorem
X is normally distributed
with mean µ,
and with standard deviation
√σ .
n
µ
µ+
σ
√
n
Empirical Rule
Confidence Intervals
Finding a good sample size
Recall the Central Limit Theorem
Population Distribution
Mean µ
Standard deviation σ
µ
Distribution of X
Mean µ
Standard deviation
σ
√
n
µ−
σ
√
n
Central Limit Theorem
µ+
σ
√
n
We call this the
standard error.
X is normally distributed
with mean µ,
and with standard deviation
µ
√σ .
n
Empirical Rule
Confidence Intervals
Finding a good sample size
So our sample mean x is chosen at random from this
distribution:
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
σ
µ + 2√
n
σ
µ + 3√
n
Empirical Rule
Confidence Intervals
Finding a good sample size
So our sample mean x is chosen at random from this
distribution:
95%
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
σ
µ + 2√
n
σ
µ + 3√
n
That means 95% of the time, our sample mean will be less than
2 standard errors from the population mean µ.
Empirical Rule
Confidence Intervals
Finding a good sample size
So our sample mean x is chosen at random from this
distribution:
95%
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
σ
µ + 2√
n
σ
µ + 3√
n
That means 95% of the time, our sample mean will be less than
2 standard errors from the population mean µ.
Empirical Rule
Confidence Intervals
Finding a good sample size
95% of the time. . .
x is between µ − 2 √σn and µ + 2 √σn .
µ − 2 √σn
µ + 2 √σn
µ
x
Empirical Rule
Confidence Intervals
Finding a good sample size
95% of the time. . .
x is between µ − 2 √σn and µ + 2 √σn .
µ − 2 √σn
µ + 2 √σn
µ
x
I.e., x is no farther away from µ than 2 √σn .
σ
< 2√
n
µ
x
Empirical Rule
Confidence Intervals
Finding a good sample size
95% of the time. . .
x is between µ − 2 √σn and µ + 2 √σn .
µ − 2 √σn
µ + 2 √σn
µ
x
I.e., x is no farther away from µ than 2 √σn .
σ
< 2√
n
µ
x
I.e., µ is no farther away from x than 2 √σn .
Empirical Rule
Confidence Intervals
Finding a good sample size
95% of the time. . .
x is between µ − 2 √σn and µ + 2 √σn .
µ − 2 √σn
µ + 2 √σn
µ
x
I.e., x is no farther away from µ than 2 √σn .
σ
< 2√
n
µ
x
I.e., µ is no farther away from x than 2 √σn .
I.e., µ is between x − 2 √σn and x + 2 √σn .
x − 2 √σn
x + 2 √σn
µ
x
Empirical Rule
Confidence Intervals
Finding a good sample size
Our first confidence interval
x
Now the perspective from the ground!
I took my sample and got my x.
I know that 95% of the times I do that, the real µ is
somewhere between x − 2 √σn and x + 2 √σn .
So I am 95% confident that µ is somewhere in that interval!
This is my 95% confidence interval.
Empirical Rule
Confidence Intervals
Finding a good sample size
Our first confidence interval
x − 2 √σn
x + 2 √σn
x
Now the perspective from the ground!
I took my sample and got my x.
I know that 95% of the times I do that, the real µ is
somewhere between x − 2 √σn and x + 2 √σn .
So I am 95% confident that µ is somewhere in that interval!
This is my 95% confidence interval.
Empirical Rule
Confidence Intervals
Finding a good sample size
Our first confidence interval
x − 2 √σn
x + 2 √σn
µ
x
Now the perspective from the ground!
I took my sample and got my x.
I know that 95% of the times I do that, the real µ is
somewhere between x − 2 √σn and x + 2 √σn .
So I am 95% confident that µ is somewhere in that interval!
This is my 95% confidence interval.
Empirical Rule
Confidence Intervals
Finding a good sample size
Our first confidence interval
x − 2 √σn
x + 2 √σn
µ
x
Now the perspective from the ground!
I took my sample and got my x.
I know that 95% of the times I do that, the real µ is
somewhere between x − 2 √σn and x + 2 √σn .
So I am 95% confident that µ is somewhere in that interval!
This is my 95% confidence interval.
Empirical Rule
Confidence Intervals
Finding a good sample size
The 95% Confidence Interval
Definition
Suppose we have a population with a standard deviation σ.
We take a random sample of size n and compute the sample
mean x. Then
σ
σ
x − 2√ , x + 2√
,
n
n
which means the range of numbers from x − 2 √σn to x + 2 √σn ,
is the 95% confidence interval for µ.
That means we are 95% confident that the true population
mean µ is somewhere in that range of numbers.
Empirical Rule
Confidence Intervals
Finding a good sample size
The 95% Confidence Interval
Definition
Suppose we have a population with a standard deviation σ.
We take a random sample of size n and compute the sample
mean x. Then
σ
σ
x − 2√ , x + 2√
,
n
n
which means the range of numbers from x − 2 √σn to x + 2 √σn ,
is the 95% confidence interval for µ.
That means we are 95% confident that the true population
mean µ is somewhere in that range of numbers.
Empirical Rule
Confidence Intervals
Finding a good sample size
What about σ?
σ
σ
x − 2√ , x + 2√
,
n
n
You might object at this point, because our formula still has
σ in it!
We do know the sample mean x, and we do know the
sample size n.
However, if we don’t know the population mean µ, how on
earth would we know the population standard deviation σ?
We’ll learn in the next class period how to get rid of σ. For
now, we’ll just pretend.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example
Example
A magazine surveyed 1200 students from 100 colleges about how much time
they spend on the Internet per week. The magazine reported that the
average was 15.1 hours. Assuming the population standard deviation is 5
hours, construct a 95% confidence interval for this statistic.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example
Example
A magazine surveyed 1200 students from 100 colleges about how much time
they spend on the Internet per week. The magazine reported that the
average was 15.1 hours. Assuming the population standard deviation is 5
hours, construct a 95% confidence interval for this statistic.
Solution
We see that n = 1200, x = 15.1, and σ = 5, so the standard error is
σ
5
√
= √1200
= 0.1444. We know a 95% confidence interval is
n
x − 2 √σn , x + 2 √σn ,
which is
(15.1 − 2(0.1444), 15.1 + 2(0.1444))
or just (14.81, 15.39). Thus the magazine can be 95% confident that
the true population mean is somewhere between 14.81 hours and
15.39 hours.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example
Example
A magazine surveyed 1200 students from 100 colleges about how much time
they spend on the Internet per week. The magazine reported that the
average was 15.1 hours. Assuming the population standard deviation is 5
hours, construct a 95% confidence interval for this statistic.
Solution
We see that n = 1200, x = 15.1, and σ = 5, so the standard error is
σ
5
√
= √1200
= 0.1444. We know a 95% confidence interval is
n
x − 2 √σn , x + 2 √σn ,
which is
(15.1 − 2(0.1444), 15.1 + 2(0.1444))
or just (14.81, 15.39). Thus the magazine can be 95% confident that
the true population mean is somewhere between 14.81 hours and
15.39 hours.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example
Example
A magazine surveyed 1200 students from 100 colleges about how much time
they spend on the Internet per week. The magazine reported that the
average was 15.1 hours. Assuming the population standard deviation is 5
hours, construct a 95% confidence interval for this statistic.
Solution
We see that n = 1200, x = 15.1, and σ = 5, so the standard error is
σ
5
√
= √1200
= 0.1444. We know a 95% confidence interval is
n
x − 2 √σn , x + 2 √σn ,
which is
(15.1 − 2(0.1444), 15.1 + 2(0.1444))
or just (14.81, 15.39). Thus the magazine can be 95% confident that
the true population mean is somewhere between 14.81 hours and
15.39 hours.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example
Example
A magazine surveyed 1200 students from 100 colleges about how much time
they spend on the Internet per week. The magazine reported that the
average was 15.1 hours. Assuming the population standard deviation is 5
hours, construct a 95% confidence interval for this statistic.
Solution
We see that n = 1200, x = 15.1, and σ = 5, so the standard error is
σ
5
√
= √1200
= 0.1444. We know a 95% confidence interval is
n
x − 2 √σn , x + 2 √σn ,
which is
(15.1 − 2(0.1444), 15.1 + 2(0.1444))
or just (14.81, 15.39). Thus the magazine can be 95% confident that
the true population mean is somewhere between 14.81 hours and
15.39 hours.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example
Example
A magazine surveyed 1200 students from 100 colleges about how much time
they spend on the Internet per week. The magazine reported that the
average was 15.1 hours. Assuming the population standard deviation is 5
hours, construct a 95% confidence interval for this statistic.
Solution
We see that n = 1200, x = 15.1, and σ = 5, so the standard error is
σ
5
√
= √1200
= 0.1444. We know a 95% confidence interval is
n
x − 2 √σn , x + 2 √σn ,
which is
(15.1 − 2(0.1444), 15.1 + 2(0.1444))
or just (14.81, 15.39). Thus the magazine can be 95% confident that
the true population mean is somewhere between 14.81 hours and
15.39 hours.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example
Example
A magazine surveyed 1200 students from 100 colleges about how much time
they spend on the Internet per week. The magazine reported that the
average was 15.1 hours. Assuming the population standard deviation is 5
hours, construct a 95% confidence interval for this statistic.
Solution
We see that n = 1200, x = 15.1, and σ = 5, so the standard error is
σ
5
√
= √1200
= 0.1444. We know a 95% confidence interval is
n
x − 2 √σn , x + 2 √σn ,
which is
(15.1 − 2(0.1444), 15.1 + 2(0.1444))
or just (14.81, 15.39). Thus the magazine can be 95% confident that
the true population mean is somewhere between 14.81 hours and
15.39 hours.
Empirical Rule
Confidence Intervals
What about other numbers?
What if we want to be more confident?
Finding a good sample size
Empirical Rule
Confidence Intervals
Finding a good sample size
What about other numbers?
What if we want to be more confident?
We chose 2 √σn because 95% of the time, x is that close to µ.
95%
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
σ
µ + 2√
n
σ
µ + 3√
n
Empirical Rule
Confidence Intervals
Finding a good sample size
What about other numbers?
What if we want to be more confident?
We chose 2 √σn because 95% of the time, x is that close to µ.
95%
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
What if we wanted to be 99.7% sure?
σ
µ + 2√
n
σ
µ + 3√
n
Empirical Rule
Confidence Intervals
Finding a good sample size
What about other numbers?
What if we want to be more confident?
We chose 2 √σn because 95% of the time, x is that close to µ.
99.7%
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
σ
µ + 2√
n
σ
µ + 3√
n
What if we wanted to be 99.7% sure? Use 3 standard
errors.
Empirical Rule
Confidence Intervals
Finding a good sample size
What about other numbers?
What if we want to be more confident?
We chose 2 √σn because 95% of the time, x is that close to µ.
99.7%
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
σ
µ + 2√
n
σ
µ + 3√
n
What if we wanted to be 99.7% sure? Use 3 standard
errors.
What if we wanted to be 68% sure?
Empirical Rule
Confidence Intervals
Finding a good sample size
What about other numbers?
What if we want to be more confident?
We chose 2 √σn because 95% of the time, x is that close to µ.
68%
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
σ
µ + 2√
n
σ
µ + 3√
n
What if we wanted to be 99.7% sure? Use 3 standard
errors.
What if we wanted to be 68% sure? Use 1 standard error.
Empirical Rule
Confidence Intervals
Finding a good sample size
What about other numbers?
What if we want to be more confident?
We chose 2 √σn because 95% of the time, x is that close to µ.
68%
σ
µ − 3√
n
σ
µ − 2√
n
σ
µ− √
n
µ
σ
µ+ √
n
σ
µ + 2√
n
σ
µ + 3√
n
What if we wanted to be 99.7% sure? Use 3 standard
errors.
What if we wanted to be 68% sure? Use 1 standard error.
What if we wanted a different percentage?
Empirical Rule
Confidence Intervals
Finding a good sample size
How to find a y -confidence interval
(e.g., for a 92% confidence interval, y = 0.92)
1
Draw the standard normal curve Z .
2
Draw two vertical bars symmetrically on the graph, and
label the middle with y .
3
That means the remaining area is 1 − y .
4
That means the left tail has area
5
Use the z-table (backwards) to learn where that tail ends!
6
Use that many standard errors!
1−y
2 .
Empirical Rule
Confidence Intervals
Finding a good sample size
How to find a y -confidence interval
(e.g., for a 92% confidence interval, y = 0.92)
1
Draw the standard normal curve Z .
2
Draw two vertical bars symmetrically on the graph, and
label the middle with y .
3
That means the remaining area is 1 − y .
4
That means the left tail has area
5
Use the z-table (backwards) to learn where that tail ends!
6
Use that many standard errors!
1−y
2 .
Empirical Rule
Confidence Intervals
Finding a good sample size
How to find a y -confidence interval
(e.g., for a 92% confidence interval, y = 0.92)
1
Draw the standard normal curve Z .
y
2
Draw two vertical bars symmetrically on the graph, and
label the middle with y .
3
That means the remaining area is 1 − y .
4
That means the left tail has area
5
Use the z-table (backwards) to learn where that tail ends!
6
Use that many standard errors!
1−y
2 .
Empirical Rule
Confidence Intervals
Finding a good sample size
How to find a y -confidence interval
(e.g., for a 92% confidence interval, y = 0.92)
1
Draw the standard normal curve Z .
1−y
y
2
Draw two vertical bars symmetrically on the graph, and
label the middle with y .
3
That means the remaining area is 1 − y .
4
That means the left tail has area
5
Use the z-table (backwards) to learn where that tail ends!
6
Use that many standard errors!
1−y
2 .
Empirical Rule
Confidence Intervals
Finding a good sample size
How to find a y -confidence interval
(e.g., for a 92% confidence interval, y = 0.92)
1
Draw the standard normal curve Z .
1−y
2
1−y
y
2
Draw two vertical bars symmetrically on the graph, and
label the middle with y .
3
That means the remaining area is 1 − y .
4
That means the left tail has area
5
Use the z-table (backwards) to learn where that tail ends!
6
Use that many standard errors!
1−y
2 .
Empirical Rule
Confidence Intervals
Finding a good sample size
How to find a y -confidence interval
(e.g., for a 92% confidence interval, y = 0.92)
1
Draw the standard normal curve Z .
1−y
2
1−y
y
−z
2
Draw two vertical bars symmetrically on the graph, and
label the middle with y .
3
That means the remaining area is 1 − y .
4
That means the left tail has area
5
Use the z-table (backwards) to learn where that tail ends!
6
Use that many standard errors!
1−y
2 .
Empirical Rule
Confidence Intervals
Finding a good sample size
How to find a y -confidence interval
(e.g., for a 92% confidence interval, y = 0.92)
1
Draw the standard normal curve Z .
1−y
2
1−y
y
−z
2
Draw two vertical bars symmetrically on the graph, and
label the middle with y .
3
That means the remaining area is 1 − y .
4
That means the left tail has area
5
Use the z-table (backwards) to learn where that tail ends!
6
Use that many standard errors!
1−y
2 .
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
Example
Dr. McKnight is studying the length of human pregnancies,
which have a standard deviation of 14 days. She studies a
random sample of 50 pregnancies, and discovers that the
sample mean is 274 days. What is the 98% confidence
interval?
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
Example
Dr. McKnight is studying the length of human pregnancies,
which have a standard deviation of 14 days. She studies a
random sample of 50 pregnancies, and discovers that the
sample mean is 274 days. What is the 98% confidence
interval?
Solution
Let’s follow our procedure!
...
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
We need a 98% confidence interval.
1
Draw the standard normal curve Z .
2
Draw vertical bars and label the middle with 0.98.
3
That means the remaining area is 1 − 0.98 = 0.02.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -2.33.
6
So we need 2.33 standard errors!
0.02
2
= 0.01.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
We need a 98% confidence interval.
1
Draw the standard normal curve Z .
2
Draw vertical bars and label the middle with 0.98.
3
That means the remaining area is 1 − 0.98 = 0.02.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -2.33.
6
So we need 2.33 standard errors!
0.02
2
= 0.01.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
We need a 98% confidence interval.
1
Draw the standard normal curve Z .
0.98
2
Draw vertical bars and label the middle with 0.98.
3
That means the remaining area is 1 − 0.98 = 0.02.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -2.33.
6
So we need 2.33 standard errors!
0.02
2
= 0.01.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
We need a 98% confidence interval.
1
Draw the standard normal curve Z .
0.02
0.98
2
Draw vertical bars and label the middle with 0.98.
3
That means the remaining area is 1 − 0.98 = 0.02.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -2.33.
6
So we need 2.33 standard errors!
0.02
2
= 0.01.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
We need a 98% confidence interval.
1
Draw the standard normal curve Z .
0.01
0.02
0.98
2
Draw vertical bars and label the middle with 0.98.
3
That means the remaining area is 1 − 0.98 = 0.02.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -2.33.
6
So we need 2.33 standard errors!
0.02
2
= 0.01.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
We need a 98% confidence interval.
1
Draw the standard normal curve Z .
0.01
0.02
0.98
−2.33
2
Draw vertical bars and label the middle with 0.98.
3
That means the remaining area is 1 − 0.98 = 0.02.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -2.33.
6
So we need 2.33 standard errors!
0.02
2
= 0.01.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
We need a 98% confidence interval.
1
Draw the standard normal curve Z .
0.01
0.02
0.98
−2.33
2
Draw vertical bars and label the middle with 0.98.
3
That means the remaining area is 1 − 0.98 = 0.02.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -2.33.
6
So we need 2.33 standard errors!
0.02
2
= 0.01.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
Example
Dr. McKnight is studying the length of human pregnancies, which have a standard
deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers
the sample mean is 274 days. What is the 98% confidence interval?
Solution, cont.
Thus we need 2.33 standard errors to get 98% confidence.
So the confidence interval is
σ
σ
x − 2.33 √ , x + 2.33 √
n
n
14
14
=
274 − 2.33 · √ , 274 + 2.33 · √
50
50
= (269.4, 278.6).
Thus Dr. McKnight can be 98% sure that the true population
mean is between 269.4 days and 278.6 days.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
Example
Dr. McKnight is studying the length of human pregnancies, which have a standard
deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers
the sample mean is 274 days. What is the 98% confidence interval?
Solution, cont.
Thus we need 2.33 standard errors to get 98% confidence.
So the confidence interval is
σ
σ
x − 2.33 √ , x + 2.33 √
n
n
14
14
=
274 − 2.33 · √ , 274 + 2.33 · √
50
50
= (269.4, 278.6).
Thus Dr. McKnight can be 98% sure that the true population
mean is between 269.4 days and 278.6 days.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
Example
Dr. McKnight is studying the length of human pregnancies, which have a standard
deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers
the sample mean is 274 days. What is the 98% confidence interval?
Solution, cont.
Thus we need 2.33 standard errors to get 98% confidence.
So the confidence interval is
σ
σ
x − 2.33 √ , x + 2.33 √
n
n
14
14
=
274 − 2.33 · √ , 274 + 2.33 · √
50
50
= (269.4, 278.6).
Thus Dr. McKnight can be 98% sure that the true population
mean is between 269.4 days and 278.6 days.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
Example
Dr. McKnight is studying the length of human pregnancies, which have a standard
deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers
the sample mean is 274 days. What is the 98% confidence interval?
Solution, cont.
Thus we need 2.33 standard errors to get 98% confidence.
So the confidence interval is
σ
σ
x − 2.33 √ , x + 2.33 √
n
n
14
14
=
274 − 2.33 · √ , 274 + 2.33 · √
50
50
= (269.4, 278.6).
Thus Dr. McKnight can be 98% sure that the true population
mean is between 269.4 days and 278.6 days.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pregnancy
Example
Dr. McKnight is studying the length of human pregnancies, which have a standard
deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers
the sample mean is 274 days. What is the 98% confidence interval?
Solution, cont.
Thus we need 2.33 standard errors to get 98% confidence.
So the confidence interval is
σ
σ
x − 2.33 √ , x + 2.33 √
n
n
14
14
=
274 − 2.33 · √ , 274 + 2.33 · √
50
50
= (269.4, 278.6).
Thus Dr. McKnight can be 98% sure that the true population
mean is between 269.4 days and 278.6 days.
Empirical Rule
Confidence Intervals
Outline
1
Empirical Rule
2
Confidence Intervals
3
Finding a good sample size
Finding a good sample size
Empirical Rule
Confidence Intervals
Finding a good sample size
Finding a good sample size
When you’re planning to conduct an experiment, it’s important
to get a large enough sample size.
Example
An environmental scientist is studying the pollution levels in a
stream. He wants to know how many samples he should take
to be 90% sure that his estimate x differs from the true value µ
by no more than 1.5 µg/liter. (The standard deviation of the
pollution levels is 6 µg/liter.) How many samples should he
take?
Empirical Rule
Confidence Intervals
Finding a good sample size
Finding a good sample size
When you’re planning to conduct an experiment, it’s important
to get a large enough sample size.
Example
An environmental scientist is studying the pollution levels in a
stream. He wants to know how many samples he should take
to be 90% sure that his estimate x differs from the true value µ
by no more than 1.5 µg/liter. (The standard deviation of the
pollution levels is 6 µg/liter.) How many samples should he
take?
Solution
First, we need to find out what a 90% confidence interval
looks like.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
We need a 90% confidence interval.
1
Draw the standard normal curve Z .
2
Draw vertical bars and label the middle with 0.90.
3
That means the remaining area is 1 − 0.90 = 0.10.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -1.65.
6
So we need 1.65 standard errors!
0.10
2
= 0.05.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
We need a 90% confidence interval.
1
Draw the standard normal curve Z .
2
Draw vertical bars and label the middle with 0.90.
3
That means the remaining area is 1 − 0.90 = 0.10.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -1.65.
6
So we need 1.65 standard errors!
0.10
2
= 0.05.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
We need a 90% confidence interval.
1
Draw the standard normal curve Z .
0.90
2
Draw vertical bars and label the middle with 0.90.
3
That means the remaining area is 1 − 0.90 = 0.10.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -1.65.
6
So we need 1.65 standard errors!
0.10
2
= 0.05.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
We need a 90% confidence interval.
1
Draw the standard normal curve Z .
0.10
0.90
2
Draw vertical bars and label the middle with 0.90.
3
That means the remaining area is 1 − 0.90 = 0.10.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -1.65.
6
So we need 1.65 standard errors!
0.10
2
= 0.05.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
We need a 90% confidence interval.
1
Draw the standard normal curve Z .
0.05
0.10
0.90
2
Draw vertical bars and label the middle with 0.90.
3
That means the remaining area is 1 − 0.90 = 0.10.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -1.65.
6
So we need 1.65 standard errors!
0.10
2
= 0.05.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
We need a 90% confidence interval.
1
Draw the standard normal curve Z .
0.05
0.10
0.90
−1.65
2
Draw vertical bars and label the middle with 0.90.
3
That means the remaining area is 1 − 0.90 = 0.10.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -1.65.
6
So we need 1.65 standard errors!
0.10
2
= 0.05.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
We need a 90% confidence interval.
1
Draw the standard normal curve Z .
0.05
0.10
0.90
−1.65
2
Draw vertical bars and label the middle with 0.90.
3
That means the remaining area is 1 − 0.90 = 0.10.
4
That means the left tail has area
5
The z-table (backwards) tells us the tail ends at -1.65.
6
So we need 1.65 standard errors!
0.10
2
= 0.05.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
σ
6
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
σ
6
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
6
σ
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
6
σ
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
6
σ
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
6
σ
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
6
σ
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
6
σ
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
6
σ
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.
Empirical Rule
Confidence Intervals
Finding a good sample size
Example: Pollution
Example
An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he
should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The
standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take?
Solution, cont.
So the scientist can be 90% confident that the difference between x
and µ is no more than 1.65 standard errors.
He wants that maximum difference to be 1.5 µg/liter, i.e.,
6
σ
1.5 = 1.65 √ = 1.65 √
n
n
(plugging in σ = 6). We need to find n.
√
1.5√n = 1.65 · 6
n = 9.9 ÷ 1.5
n = 6.62
=
=
=
9.9
6.6
43.56
Thus the scientist must take at least 44 samples.