* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Confidence Intervals for Means
Survey
Document related concepts
Transcript
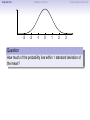
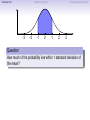
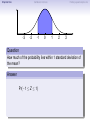
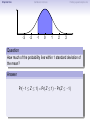
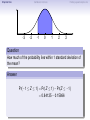
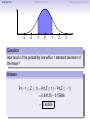
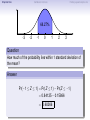
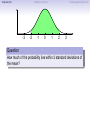
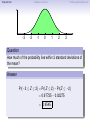
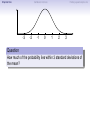
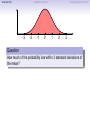
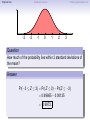
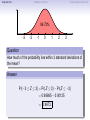
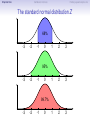
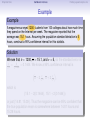
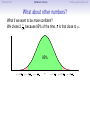
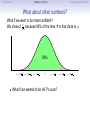
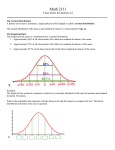
Empirical Rule Confidence Intervals Outline 1 Empirical Rule 2 Confidence Intervals 3 Finding a good sample size Finding a good sample size Empirical Rule Confidence Intervals Outline 1 Empirical Rule 2 Confidence Intervals 3 Finding a good sample size Finding a good sample size Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 1 standard deviation of the mean? Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 1 standard deviation of the mean? Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 1 standard deviation of the mean? Answer Pr(−1 ≤ Z ≤ 1) Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 1 standard deviation of the mean? Answer Pr(−1 ≤ Z ≤ 1) = Pr(Z ≤ 1) − Pr(Z ≤ −1) Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 1 standard deviation of the mean? Answer Pr(−1 ≤ Z ≤ 1) = Pr(Z ≤ 1) − Pr(Z ≤ −1) = 0.84135 − 0.15866 Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 1 standard deviation of the mean? Answer Pr(−1 ≤ Z ≤ 1) = Pr(Z ≤ 1) − Pr(Z ≤ −1) = 0.84135 − 0.15866 = 0.68269. Empirical Rule Confidence Intervals Finding a good sample size 68.27% -3 -2 -1 0 1 2 3 Question How much of the probability lies within 1 standard deviation of the mean? Answer Pr(−1 ≤ Z ≤ 1) = Pr(Z ≤ 1) − Pr(Z ≤ −1) = 0.84135 − 0.15866 = 0.68269. Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 2 standard deviations of the mean? Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 2 standard deviations of the mean? Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 2 standard deviations of the mean? Answer Pr(−2 ≤ Z ≤ 2) = Pr(Z ≤ 2) − Pr(Z ≤ −2) = 0.97725 − 0.02275 = 0.9545. Empirical Rule Confidence Intervals Finding a good sample size 95.45% -3 -2 -1 0 1 2 3 Question How much of the probability lies within 2 standard deviations of the mean? Answer Pr(−2 ≤ Z ≤ 2) = Pr(Z ≤ 2) − Pr(Z ≤ −2) = 0.97725 − 0.02275 = 0.9545. Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 3 standard deviations of the mean? Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 3 standard deviations of the mean? Empirical Rule Confidence Intervals -3 -2 -1 0 Finding a good sample size 1 2 3 Question How much of the probability lies within 3 standard deviations of the mean? Answer Pr(−3 ≤ Z ≤ 3) = Pr(Z ≤ 3) − Pr(Z ≤ −3) = 0.99865 − 0.00135 = 0.9973. Empirical Rule Confidence Intervals Finding a good sample size 99.73% -3 -2 -1 0 1 2 3 Question How much of the probability lies within 3 standard deviations of the mean? Answer Pr(−3 ≤ Z ≤ 3) = Pr(Z ≤ 3) − Pr(Z ≤ −3) = 0.99865 − 0.00135 = 0.9973. Empirical Rule Confidence Intervals Finding a good sample size The standard normal distribution Z 68% -3 -2 -1 0 1 2 3 1 2 3 1 2 3 95% -3 -2 -1 0 99.7% -3 -2 -1 0 Empirical Rule Confidence Intervals Finding a good sample size Any normal distribution X 68% µ − 3σ µ − 2σ µ − σ µ µ + σ µ + 2σ µ + 3σ 95% µ − 3σ µ − 2σ µ − σ µ µ + σ µ + 2σ µ + 3σ 99.7% µ − 3σ µ − 2σ µ − σ µ µ + σ µ + 2σ µ + 3σ Empirical Rule Confidence Intervals Finding a good sample size Empirical Rule If X is a normal random variable with standard deviation σ, 68% of the probability is within σ of the mean. 95% of the probability is within 2σ of the mean. 99.7% of the probability is within 3σ of the mean. Empirical Rule Confidence Intervals Finding a good sample size Example Problem We now can get approximate answers to some problems without the z-table! Example The heights of men aged 20 to 29 are approximately normal with mean 6900 and standard deviation 2.800 . 1 About what percentage of these men measure between 6600 and 7200 ? 2 Find a range of heights that contains 95% of these men. Empirical Rule Confidence Intervals Finding a good sample size Example Problem We now can get approximate answers to some problems without the z-table! Example The heights of men aged 20 to 29 are approximately normal with mean 6900 and standard deviation 2.800 . 1 About what percentage of these men measure between 6600 and 7200 ? 2 Find a range of heights that contains 95% of these men. Solution 1 µ = 69 and σ = 2.8, so 6600 is about one standard deviation below the mean and 7200 is about one standard deviation above the mean. Thus, by the Empirical Rule, a little more than 68% of the men fall within that range. (Exact answer: 71.5%) Empirical Rule Confidence Intervals Finding a good sample size Example Problem We now can get approximate answers to some problems without the z-table! Example The heights of men aged 20 to 29 are approximately normal with mean 6900 and standard deviation 2.800 . 1 About what percentage of these men measure between 6600 and 7200 ? 2 Find a range of heights that contains 95% of these men. Solution 1 µ = 69 and σ = 2.8, so 6600 is about one standard deviation below the mean and 7200 is about one standard deviation above the mean. Thus, by the Empirical Rule, a little more than 68% of the men fall within that range. (Exact answer: 71.5%) Empirical Rule Confidence Intervals Finding a good sample size Example Problem Example The heights of men aged 20 to 29 are approximately normal with mean 6900 and standard deviation 2.800 . 1 About what percentage of these men measure between 6600 and 7200 ? 2 Find a range of heights that contains 95% of these men. Solution, cont. 2 By the Empirical Rule, 95% of the men fall within the range from µ − 2σ to µ + 2σ. Thus the range from 69 − 2 · 2.8 = 63.4 to 69 + 2 · 2.8 = 74.6 contains 95% of the men, so our answer is “63.4 to 74.6 inches.” (More exact answer: 63.51 to 74.49 inches.) Empirical Rule Confidence Intervals Finding a good sample size Example Problem Example The heights of men aged 20 to 29 are approximately normal with mean 6900 and standard deviation 2.800 . 1 About what percentage of these men measure between 6600 and 7200 ? 2 Find a range of heights that contains 95% of these men. Solution, cont. 2 By the Empirical Rule, 95% of the men fall within the range from µ − 2σ to µ + 2σ. Thus the range from 69 − 2 · 2.8 = 63.4 to 69 + 2 · 2.8 = 74.6 contains 95% of the men, so our answer is “63.4 to 74.6 inches.” (More exact answer: 63.51 to 74.49 inches.) Empirical Rule Confidence Intervals Finding a good sample size Example Problem Example The heights of men aged 20 to 29 are approximately normal with mean 6900 and standard deviation 2.800 . 1 About what percentage of these men measure between 6600 and 7200 ? 2 Find a range of heights that contains 95% of these men. Solution, cont. 2 By the Empirical Rule, 95% of the men fall within the range from µ − 2σ to µ + 2σ. Thus the range from 69 − 2 · 2.8 = 63.4 to 69 + 2 · 2.8 = 74.6 contains 95% of the men, so our answer is “63.4 to 74.6 inches.” (More exact answer: 63.51 to 74.49 inches.) Empirical Rule Confidence Intervals Outline 1 Empirical Rule 2 Confidence Intervals 3 Finding a good sample size Finding a good sample size Empirical Rule Confidence Intervals Finding a good sample size How good is a sample mean x? Say we have a population and we want to know its mean µ. So we choose a sample, measure it, and compute the sample mean x. Of course x could be larger or smaller than µ. How likely is it to be close to µ? Empirical Rule Confidence Intervals Finding a good sample size Recall the Central Limit Theorem Population Distribution Mean µ Standard deviation σ µ Central Limit Theorem X is normally distributed with mean µ, and with standard deviation √σ . n Empirical Rule Confidence Intervals Finding a good sample size Recall the Central Limit Theorem Population Distribution Mean µ Standard deviation σ µ Distribution of X Mean µ Standard deviation σ √ n µ Central Limit Theorem X is normally distributed with mean µ, and with standard deviation √σ . n Empirical Rule Confidence Intervals Finding a good sample size Recall the Central Limit Theorem Population Distribution Mean µ Standard deviation σ µ Distribution of X Mean µ Standard deviation σ √ n µ Central Limit Theorem X is normally distributed with mean µ, and with standard deviation √σ . n Empirical Rule Confidence Intervals Finding a good sample size Recall the Central Limit Theorem Population Distribution Mean µ Standard deviation σ µ Distribution of X Mean µ Standard deviation σ √ n µ− σ √ n Central Limit Theorem X is normally distributed with mean µ, and with standard deviation √σ . n µ µ+ σ √ n Empirical Rule Confidence Intervals Finding a good sample size Recall the Central Limit Theorem Population Distribution Mean µ Standard deviation σ µ Distribution of X Mean µ Standard deviation σ √ n µ− σ √ n Central Limit Theorem µ+ σ √ n We call this the standard error. X is normally distributed with mean µ, and with standard deviation µ √σ . n Empirical Rule Confidence Intervals Finding a good sample size So our sample mean x is chosen at random from this distribution: σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n σ µ + 2√ n σ µ + 3√ n Empirical Rule Confidence Intervals Finding a good sample size So our sample mean x is chosen at random from this distribution: 95% σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n σ µ + 2√ n σ µ + 3√ n That means 95% of the time, our sample mean will be less than 2 standard errors from the population mean µ. Empirical Rule Confidence Intervals Finding a good sample size So our sample mean x is chosen at random from this distribution: 95% σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n σ µ + 2√ n σ µ + 3√ n That means 95% of the time, our sample mean will be less than 2 standard errors from the population mean µ. Empirical Rule Confidence Intervals Finding a good sample size 95% of the time. . . x is between µ − 2 √σn and µ + 2 √σn . µ − 2 √σn µ + 2 √σn µ x Empirical Rule Confidence Intervals Finding a good sample size 95% of the time. . . x is between µ − 2 √σn and µ + 2 √σn . µ − 2 √σn µ + 2 √σn µ x I.e., x is no farther away from µ than 2 √σn . σ < 2√ n µ x Empirical Rule Confidence Intervals Finding a good sample size 95% of the time. . . x is between µ − 2 √σn and µ + 2 √σn . µ − 2 √σn µ + 2 √σn µ x I.e., x is no farther away from µ than 2 √σn . σ < 2√ n µ x I.e., µ is no farther away from x than 2 √σn . Empirical Rule Confidence Intervals Finding a good sample size 95% of the time. . . x is between µ − 2 √σn and µ + 2 √σn . µ − 2 √σn µ + 2 √σn µ x I.e., x is no farther away from µ than 2 √σn . σ < 2√ n µ x I.e., µ is no farther away from x than 2 √σn . I.e., µ is between x − 2 √σn and x + 2 √σn . x − 2 √σn x + 2 √σn µ x Empirical Rule Confidence Intervals Finding a good sample size Our first confidence interval x Now the perspective from the ground! I took my sample and got my x. I know that 95% of the times I do that, the real µ is somewhere between x − 2 √σn and x + 2 √σn . So I am 95% confident that µ is somewhere in that interval! This is my 95% confidence interval. Empirical Rule Confidence Intervals Finding a good sample size Our first confidence interval x − 2 √σn x + 2 √σn x Now the perspective from the ground! I took my sample and got my x. I know that 95% of the times I do that, the real µ is somewhere between x − 2 √σn and x + 2 √σn . So I am 95% confident that µ is somewhere in that interval! This is my 95% confidence interval. Empirical Rule Confidence Intervals Finding a good sample size Our first confidence interval x − 2 √σn x + 2 √σn µ x Now the perspective from the ground! I took my sample and got my x. I know that 95% of the times I do that, the real µ is somewhere between x − 2 √σn and x + 2 √σn . So I am 95% confident that µ is somewhere in that interval! This is my 95% confidence interval. Empirical Rule Confidence Intervals Finding a good sample size Our first confidence interval x − 2 √σn x + 2 √σn µ x Now the perspective from the ground! I took my sample and got my x. I know that 95% of the times I do that, the real µ is somewhere between x − 2 √σn and x + 2 √σn . So I am 95% confident that µ is somewhere in that interval! This is my 95% confidence interval. Empirical Rule Confidence Intervals Finding a good sample size The 95% Confidence Interval Definition Suppose we have a population with a standard deviation σ. We take a random sample of size n and compute the sample mean x. Then σ σ x − 2√ , x + 2√ , n n which means the range of numbers from x − 2 √σn to x + 2 √σn , is the 95% confidence interval for µ. That means we are 95% confident that the true population mean µ is somewhere in that range of numbers. Empirical Rule Confidence Intervals Finding a good sample size The 95% Confidence Interval Definition Suppose we have a population with a standard deviation σ. We take a random sample of size n and compute the sample mean x. Then σ σ x − 2√ , x + 2√ , n n which means the range of numbers from x − 2 √σn to x + 2 √σn , is the 95% confidence interval for µ. That means we are 95% confident that the true population mean µ is somewhere in that range of numbers. Empirical Rule Confidence Intervals Finding a good sample size What about σ? σ σ x − 2√ , x + 2√ , n n You might object at this point, because our formula still has σ in it! We do know the sample mean x, and we do know the sample size n. However, if we don’t know the population mean µ, how on earth would we know the population standard deviation σ? We’ll learn in the next class period how to get rid of σ. For now, we’ll just pretend. Empirical Rule Confidence Intervals Finding a good sample size Example Example A magazine surveyed 1200 students from 100 colleges about how much time they spend on the Internet per week. The magazine reported that the average was 15.1 hours. Assuming the population standard deviation is 5 hours, construct a 95% confidence interval for this statistic. Empirical Rule Confidence Intervals Finding a good sample size Example Example A magazine surveyed 1200 students from 100 colleges about how much time they spend on the Internet per week. The magazine reported that the average was 15.1 hours. Assuming the population standard deviation is 5 hours, construct a 95% confidence interval for this statistic. Solution We see that n = 1200, x = 15.1, and σ = 5, so the standard error is σ 5 √ = √1200 = 0.1444. We know a 95% confidence interval is n x − 2 √σn , x + 2 √σn , which is (15.1 − 2(0.1444), 15.1 + 2(0.1444)) or just (14.81, 15.39). Thus the magazine can be 95% confident that the true population mean is somewhere between 14.81 hours and 15.39 hours. Empirical Rule Confidence Intervals Finding a good sample size Example Example A magazine surveyed 1200 students from 100 colleges about how much time they spend on the Internet per week. The magazine reported that the average was 15.1 hours. Assuming the population standard deviation is 5 hours, construct a 95% confidence interval for this statistic. Solution We see that n = 1200, x = 15.1, and σ = 5, so the standard error is σ 5 √ = √1200 = 0.1444. We know a 95% confidence interval is n x − 2 √σn , x + 2 √σn , which is (15.1 − 2(0.1444), 15.1 + 2(0.1444)) or just (14.81, 15.39). Thus the magazine can be 95% confident that the true population mean is somewhere between 14.81 hours and 15.39 hours. Empirical Rule Confidence Intervals Finding a good sample size Example Example A magazine surveyed 1200 students from 100 colleges about how much time they spend on the Internet per week. The magazine reported that the average was 15.1 hours. Assuming the population standard deviation is 5 hours, construct a 95% confidence interval for this statistic. Solution We see that n = 1200, x = 15.1, and σ = 5, so the standard error is σ 5 √ = √1200 = 0.1444. We know a 95% confidence interval is n x − 2 √σn , x + 2 √σn , which is (15.1 − 2(0.1444), 15.1 + 2(0.1444)) or just (14.81, 15.39). Thus the magazine can be 95% confident that the true population mean is somewhere between 14.81 hours and 15.39 hours. Empirical Rule Confidence Intervals Finding a good sample size Example Example A magazine surveyed 1200 students from 100 colleges about how much time they spend on the Internet per week. The magazine reported that the average was 15.1 hours. Assuming the population standard deviation is 5 hours, construct a 95% confidence interval for this statistic. Solution We see that n = 1200, x = 15.1, and σ = 5, so the standard error is σ 5 √ = √1200 = 0.1444. We know a 95% confidence interval is n x − 2 √σn , x + 2 √σn , which is (15.1 − 2(0.1444), 15.1 + 2(0.1444)) or just (14.81, 15.39). Thus the magazine can be 95% confident that the true population mean is somewhere between 14.81 hours and 15.39 hours. Empirical Rule Confidence Intervals Finding a good sample size Example Example A magazine surveyed 1200 students from 100 colleges about how much time they spend on the Internet per week. The magazine reported that the average was 15.1 hours. Assuming the population standard deviation is 5 hours, construct a 95% confidence interval for this statistic. Solution We see that n = 1200, x = 15.1, and σ = 5, so the standard error is σ 5 √ = √1200 = 0.1444. We know a 95% confidence interval is n x − 2 √σn , x + 2 √σn , which is (15.1 − 2(0.1444), 15.1 + 2(0.1444)) or just (14.81, 15.39). Thus the magazine can be 95% confident that the true population mean is somewhere between 14.81 hours and 15.39 hours. Empirical Rule Confidence Intervals Finding a good sample size Example Example A magazine surveyed 1200 students from 100 colleges about how much time they spend on the Internet per week. The magazine reported that the average was 15.1 hours. Assuming the population standard deviation is 5 hours, construct a 95% confidence interval for this statistic. Solution We see that n = 1200, x = 15.1, and σ = 5, so the standard error is σ 5 √ = √1200 = 0.1444. We know a 95% confidence interval is n x − 2 √σn , x + 2 √σn , which is (15.1 − 2(0.1444), 15.1 + 2(0.1444)) or just (14.81, 15.39). Thus the magazine can be 95% confident that the true population mean is somewhere between 14.81 hours and 15.39 hours. Empirical Rule Confidence Intervals What about other numbers? What if we want to be more confident? Finding a good sample size Empirical Rule Confidence Intervals Finding a good sample size What about other numbers? What if we want to be more confident? We chose 2 √σn because 95% of the time, x is that close to µ. 95% σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n σ µ + 2√ n σ µ + 3√ n Empirical Rule Confidence Intervals Finding a good sample size What about other numbers? What if we want to be more confident? We chose 2 √σn because 95% of the time, x is that close to µ. 95% σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n What if we wanted to be 99.7% sure? σ µ + 2√ n σ µ + 3√ n Empirical Rule Confidence Intervals Finding a good sample size What about other numbers? What if we want to be more confident? We chose 2 √σn because 95% of the time, x is that close to µ. 99.7% σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n σ µ + 2√ n σ µ + 3√ n What if we wanted to be 99.7% sure? Use 3 standard errors. Empirical Rule Confidence Intervals Finding a good sample size What about other numbers? What if we want to be more confident? We chose 2 √σn because 95% of the time, x is that close to µ. 99.7% σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n σ µ + 2√ n σ µ + 3√ n What if we wanted to be 99.7% sure? Use 3 standard errors. What if we wanted to be 68% sure? Empirical Rule Confidence Intervals Finding a good sample size What about other numbers? What if we want to be more confident? We chose 2 √σn because 95% of the time, x is that close to µ. 68% σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n σ µ + 2√ n σ µ + 3√ n What if we wanted to be 99.7% sure? Use 3 standard errors. What if we wanted to be 68% sure? Use 1 standard error. Empirical Rule Confidence Intervals Finding a good sample size What about other numbers? What if we want to be more confident? We chose 2 √σn because 95% of the time, x is that close to µ. 68% σ µ − 3√ n σ µ − 2√ n σ µ− √ n µ σ µ+ √ n σ µ + 2√ n σ µ + 3√ n What if we wanted to be 99.7% sure? Use 3 standard errors. What if we wanted to be 68% sure? Use 1 standard error. What if we wanted a different percentage? Empirical Rule Confidence Intervals Finding a good sample size How to find a y -confidence interval (e.g., for a 92% confidence interval, y = 0.92) 1 Draw the standard normal curve Z . 2 Draw two vertical bars symmetrically on the graph, and label the middle with y . 3 That means the remaining area is 1 − y . 4 That means the left tail has area 5 Use the z-table (backwards) to learn where that tail ends! 6 Use that many standard errors! 1−y 2 . Empirical Rule Confidence Intervals Finding a good sample size How to find a y -confidence interval (e.g., for a 92% confidence interval, y = 0.92) 1 Draw the standard normal curve Z . 2 Draw two vertical bars symmetrically on the graph, and label the middle with y . 3 That means the remaining area is 1 − y . 4 That means the left tail has area 5 Use the z-table (backwards) to learn where that tail ends! 6 Use that many standard errors! 1−y 2 . Empirical Rule Confidence Intervals Finding a good sample size How to find a y -confidence interval (e.g., for a 92% confidence interval, y = 0.92) 1 Draw the standard normal curve Z . y 2 Draw two vertical bars symmetrically on the graph, and label the middle with y . 3 That means the remaining area is 1 − y . 4 That means the left tail has area 5 Use the z-table (backwards) to learn where that tail ends! 6 Use that many standard errors! 1−y 2 . Empirical Rule Confidence Intervals Finding a good sample size How to find a y -confidence interval (e.g., for a 92% confidence interval, y = 0.92) 1 Draw the standard normal curve Z . 1−y y 2 Draw two vertical bars symmetrically on the graph, and label the middle with y . 3 That means the remaining area is 1 − y . 4 That means the left tail has area 5 Use the z-table (backwards) to learn where that tail ends! 6 Use that many standard errors! 1−y 2 . Empirical Rule Confidence Intervals Finding a good sample size How to find a y -confidence interval (e.g., for a 92% confidence interval, y = 0.92) 1 Draw the standard normal curve Z . 1−y 2 1−y y 2 Draw two vertical bars symmetrically on the graph, and label the middle with y . 3 That means the remaining area is 1 − y . 4 That means the left tail has area 5 Use the z-table (backwards) to learn where that tail ends! 6 Use that many standard errors! 1−y 2 . Empirical Rule Confidence Intervals Finding a good sample size How to find a y -confidence interval (e.g., for a 92% confidence interval, y = 0.92) 1 Draw the standard normal curve Z . 1−y 2 1−y y −z 2 Draw two vertical bars symmetrically on the graph, and label the middle with y . 3 That means the remaining area is 1 − y . 4 That means the left tail has area 5 Use the z-table (backwards) to learn where that tail ends! 6 Use that many standard errors! 1−y 2 . Empirical Rule Confidence Intervals Finding a good sample size How to find a y -confidence interval (e.g., for a 92% confidence interval, y = 0.92) 1 Draw the standard normal curve Z . 1−y 2 1−y y −z 2 Draw two vertical bars symmetrically on the graph, and label the middle with y . 3 That means the remaining area is 1 − y . 4 That means the left tail has area 5 Use the z-table (backwards) to learn where that tail ends! 6 Use that many standard errors! 1−y 2 . Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy Example Dr. McKnight is studying the length of human pregnancies, which have a standard deviation of 14 days. She studies a random sample of 50 pregnancies, and discovers that the sample mean is 274 days. What is the 98% confidence interval? Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy Example Dr. McKnight is studying the length of human pregnancies, which have a standard deviation of 14 days. She studies a random sample of 50 pregnancies, and discovers that the sample mean is 274 days. What is the 98% confidence interval? Solution Let’s follow our procedure! ... Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy We need a 98% confidence interval. 1 Draw the standard normal curve Z . 2 Draw vertical bars and label the middle with 0.98. 3 That means the remaining area is 1 − 0.98 = 0.02. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -2.33. 6 So we need 2.33 standard errors! 0.02 2 = 0.01. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy We need a 98% confidence interval. 1 Draw the standard normal curve Z . 2 Draw vertical bars and label the middle with 0.98. 3 That means the remaining area is 1 − 0.98 = 0.02. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -2.33. 6 So we need 2.33 standard errors! 0.02 2 = 0.01. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy We need a 98% confidence interval. 1 Draw the standard normal curve Z . 0.98 2 Draw vertical bars and label the middle with 0.98. 3 That means the remaining area is 1 − 0.98 = 0.02. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -2.33. 6 So we need 2.33 standard errors! 0.02 2 = 0.01. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy We need a 98% confidence interval. 1 Draw the standard normal curve Z . 0.02 0.98 2 Draw vertical bars and label the middle with 0.98. 3 That means the remaining area is 1 − 0.98 = 0.02. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -2.33. 6 So we need 2.33 standard errors! 0.02 2 = 0.01. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy We need a 98% confidence interval. 1 Draw the standard normal curve Z . 0.01 0.02 0.98 2 Draw vertical bars and label the middle with 0.98. 3 That means the remaining area is 1 − 0.98 = 0.02. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -2.33. 6 So we need 2.33 standard errors! 0.02 2 = 0.01. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy We need a 98% confidence interval. 1 Draw the standard normal curve Z . 0.01 0.02 0.98 −2.33 2 Draw vertical bars and label the middle with 0.98. 3 That means the remaining area is 1 − 0.98 = 0.02. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -2.33. 6 So we need 2.33 standard errors! 0.02 2 = 0.01. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy We need a 98% confidence interval. 1 Draw the standard normal curve Z . 0.01 0.02 0.98 −2.33 2 Draw vertical bars and label the middle with 0.98. 3 That means the remaining area is 1 − 0.98 = 0.02. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -2.33. 6 So we need 2.33 standard errors! 0.02 2 = 0.01. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy Example Dr. McKnight is studying the length of human pregnancies, which have a standard deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers the sample mean is 274 days. What is the 98% confidence interval? Solution, cont. Thus we need 2.33 standard errors to get 98% confidence. So the confidence interval is σ σ x − 2.33 √ , x + 2.33 √ n n 14 14 = 274 − 2.33 · √ , 274 + 2.33 · √ 50 50 = (269.4, 278.6). Thus Dr. McKnight can be 98% sure that the true population mean is between 269.4 days and 278.6 days. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy Example Dr. McKnight is studying the length of human pregnancies, which have a standard deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers the sample mean is 274 days. What is the 98% confidence interval? Solution, cont. Thus we need 2.33 standard errors to get 98% confidence. So the confidence interval is σ σ x − 2.33 √ , x + 2.33 √ n n 14 14 = 274 − 2.33 · √ , 274 + 2.33 · √ 50 50 = (269.4, 278.6). Thus Dr. McKnight can be 98% sure that the true population mean is between 269.4 days and 278.6 days. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy Example Dr. McKnight is studying the length of human pregnancies, which have a standard deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers the sample mean is 274 days. What is the 98% confidence interval? Solution, cont. Thus we need 2.33 standard errors to get 98% confidence. So the confidence interval is σ σ x − 2.33 √ , x + 2.33 √ n n 14 14 = 274 − 2.33 · √ , 274 + 2.33 · √ 50 50 = (269.4, 278.6). Thus Dr. McKnight can be 98% sure that the true population mean is between 269.4 days and 278.6 days. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy Example Dr. McKnight is studying the length of human pregnancies, which have a standard deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers the sample mean is 274 days. What is the 98% confidence interval? Solution, cont. Thus we need 2.33 standard errors to get 98% confidence. So the confidence interval is σ σ x − 2.33 √ , x + 2.33 √ n n 14 14 = 274 − 2.33 · √ , 274 + 2.33 · √ 50 50 = (269.4, 278.6). Thus Dr. McKnight can be 98% sure that the true population mean is between 269.4 days and 278.6 days. Empirical Rule Confidence Intervals Finding a good sample size Example: Pregnancy Example Dr. McKnight is studying the length of human pregnancies, which have a standard deviation σ = 14 days. She studies a random sample of 50 pregnancies, and discovers the sample mean is 274 days. What is the 98% confidence interval? Solution, cont. Thus we need 2.33 standard errors to get 98% confidence. So the confidence interval is σ σ x − 2.33 √ , x + 2.33 √ n n 14 14 = 274 − 2.33 · √ , 274 + 2.33 · √ 50 50 = (269.4, 278.6). Thus Dr. McKnight can be 98% sure that the true population mean is between 269.4 days and 278.6 days. Empirical Rule Confidence Intervals Outline 1 Empirical Rule 2 Confidence Intervals 3 Finding a good sample size Finding a good sample size Empirical Rule Confidence Intervals Finding a good sample size Finding a good sample size When you’re planning to conduct an experiment, it’s important to get a large enough sample size. Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Empirical Rule Confidence Intervals Finding a good sample size Finding a good sample size When you’re planning to conduct an experiment, it’s important to get a large enough sample size. Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution First, we need to find out what a 90% confidence interval looks like. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution We need a 90% confidence interval. 1 Draw the standard normal curve Z . 2 Draw vertical bars and label the middle with 0.90. 3 That means the remaining area is 1 − 0.90 = 0.10. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -1.65. 6 So we need 1.65 standard errors! 0.10 2 = 0.05. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution We need a 90% confidence interval. 1 Draw the standard normal curve Z . 2 Draw vertical bars and label the middle with 0.90. 3 That means the remaining area is 1 − 0.90 = 0.10. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -1.65. 6 So we need 1.65 standard errors! 0.10 2 = 0.05. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution We need a 90% confidence interval. 1 Draw the standard normal curve Z . 0.90 2 Draw vertical bars and label the middle with 0.90. 3 That means the remaining area is 1 − 0.90 = 0.10. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -1.65. 6 So we need 1.65 standard errors! 0.10 2 = 0.05. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution We need a 90% confidence interval. 1 Draw the standard normal curve Z . 0.10 0.90 2 Draw vertical bars and label the middle with 0.90. 3 That means the remaining area is 1 − 0.90 = 0.10. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -1.65. 6 So we need 1.65 standard errors! 0.10 2 = 0.05. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution We need a 90% confidence interval. 1 Draw the standard normal curve Z . 0.05 0.10 0.90 2 Draw vertical bars and label the middle with 0.90. 3 That means the remaining area is 1 − 0.90 = 0.10. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -1.65. 6 So we need 1.65 standard errors! 0.10 2 = 0.05. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution We need a 90% confidence interval. 1 Draw the standard normal curve Z . 0.05 0.10 0.90 −1.65 2 Draw vertical bars and label the middle with 0.90. 3 That means the remaining area is 1 − 0.90 = 0.10. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -1.65. 6 So we need 1.65 standard errors! 0.10 2 = 0.05. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution We need a 90% confidence interval. 1 Draw the standard normal curve Z . 0.05 0.10 0.90 −1.65 2 Draw vertical bars and label the middle with 0.90. 3 That means the remaining area is 1 − 0.90 = 0.10. 4 That means the left tail has area 5 The z-table (backwards) tells us the tail ends at -1.65. 6 So we need 1.65 standard errors! 0.10 2 = 0.05. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., σ 6 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., σ 6 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., 6 σ 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., 6 σ 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., 6 σ 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., 6 σ 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., 6 σ 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., 6 σ 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., 6 σ 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples. Empirical Rule Confidence Intervals Finding a good sample size Example: Pollution Example An environmental scientist is studying the pollution levels in a stream. He wants to know how many samples he should take to be 90% sure that his estimate x differs from the true value µ by no more than 1.5 µg/liter. (The standard deviation of the pollution levels is 6 µg/liter.) How many samples should he take? Solution, cont. So the scientist can be 90% confident that the difference between x and µ is no more than 1.65 standard errors. He wants that maximum difference to be 1.5 µg/liter, i.e., 6 σ 1.5 = 1.65 √ = 1.65 √ n n (plugging in σ = 6). We need to find n. √ 1.5√n = 1.65 · 6 n = 9.9 ÷ 1.5 n = 6.62 = = = 9.9 6.6 43.56 Thus the scientist must take at least 44 samples.