* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 10. Molecules and Solids
Tight binding wikipedia , lookup
Matter wave wikipedia , lookup
Rigid rotor wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Electron configuration wikipedia , lookup
Chemical bond wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Wave–particle duality wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Mössbauer spectroscopy wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Atomic theory wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Two-dimensional nuclear magnetic resonance spectroscopy wikipedia , lookup
Population inversion wikipedia , lookup
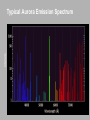
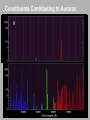
CHAPTER 9 Molecules Rotations Spectra Complex planar molecules Homework due Wednesday Nov. 4th Only 5 problems: Krane Chapter 9 Johannes Diderik van der Waals (1837 – 1923) 8, 14, 17, 20, 22 “Life ... is a relationship between molecules.” Linus Pauling Vibrational Motion: A Simple Harmonic Oscillator The Schrödinger Equation can be separated into equations for the positions of the electrons and those of the nuclei. The simple harmonic oscillator accurately describes the nuclear positions of a diatomic molecule, as well as more complex molecules. Vibrational States The energy levels are those of a quantummechanical oscillator. Evibr (n 1 2) n is called the vibrational quantum number. Don’t confuse it for n, the principal quantum number of the electronic state. Vibrational-transition selection rule: Dn = ±1 The only spectral line is ! However, deviations from a perfect parabolic potential allow other transitions (~2, ~3, …), called overtones, but they’re much weaker. Vibrational Frequencies for Various Bonds Different bonds have different vibrational frequencies (which are also affected by other nearby atoms). ← Higher energy (frequency) Wavenumber (cm-1) Notice that bonds containing Hydrogen vibrate faster because H is lighter. Water’s Vibrations Rotational States Consider diatomic molecules. A diatomic molecule may be thought of as two atoms held together with a massless, rigid rod (rigid rotator model). In a purely rotational system, the kinetic energy is expressed in terms of the angular momentum L and rotational inertia I. Erot L2 2I Rotational States L is quantized. L ( 1) where ℓ can be any integer. The energy levels are Erot 2 ( 1) 2I Erot varies only as a function of the quantum number ℓ. = ħ2/I Rotational transition energies And there is a selection rule that Dℓ = ±1. Erot 2 ( 1) 2I Transitions from ℓ +1 to ℓ : Emitted photons have energies at regular intervals: E ph 2 2I ( 1)( 2) ( 1) 2 2 3 2 2I 2 2 ( 1) I Vibration and Rotation Combined Note the difference in lengths (DE) for larger values of ℓ. E Erot Evib 2 ( 1) 1 n 2I 2 DE increases linearly with ℓ. Most transitions are forbidden by the selection rules that require Dℓ = ±1 and Dn = ±1. Note the similarity in lengths (DE) for small values of ℓ. Vibration and Rotation Combined The positions and intensities of the observed bands are ruled by quantum mechanics. Note two features in particular: 1) The relative intensities of the bands are due to different transition probabilities. 2) Some transitions are forbidden by the selection rule that requires Δℓ = ±1. Absorption spectra: Within Δℓ = ±1 rotational state changes, molecules can absorb photons and make transitions to a higher vibrational state when electromagnetic radiation is incident upon a collection of a particular kind of molecule. Vibrational/Rotational Spectrum In the absorption spectrum of HCl, the spacing between the peaks can be used to compute the rotational inertia I. The missing peak in the center corresponds to the forbidden Dℓ = 0 transition. ℓi ℓf = 1 ℓi ℓf = 1 ni nf = 1 Studying Vibrations and Rotations Infrared spectroscopy allows the study of vibrational and rotational transitions and states. But it’s often difficult to generate and detect the required IR light. It’s easier to work in the visible or near-IR. Input light DE Output light Raman scattering: If a photon of energy greater than DE is absorbed by a molecule, another photon with ±DE additional energy may be emitted. The selection rules become: Δn = 0, ±2 and Δℓ = 0, ±2 Frequencies in Atoms and Molecules Electrons vibrate in their motion around nuclei High frequency: ~1014 - 1017 cycles per second. Nuclei in molecules vibrate with respect to each other E~0.1eV Intermediate frequency: ~1011 - 1013 cycles per second. Nuclei in molecules rotate E~0.01eV Low frequency: ~109 - 1010 cycles per second. E~1eV Including Electronic Energy Levels A typical large molecule’s energy levels: E = Eelectonic + Evibrational + Erotational 2nd excited electronic state Energy 1st excited electronic state Lowest vibrational and rotational level of this electronic “manifold.” Excited vibrational and rotational level Transition Ground electronic state There are many other complications, such as spin-orbit coupling, nuclear spin, etc., which split levels. As a result, molecules generally have very complex spectra. Modeling Very Complex Molecules Sometimes more complex is actually easier! Many large organic (carbonbased) molecules are planar, and the most weakly bound electron is essentially free to move along the perimeter. We call this model the Perimeter Free-Electron Orbital model. plus inner electrons This is just a particle in a one-dimensional box! The states are just sine waves. The only difference is that x = L is the same as x = 0. So y doesn’t have to be zero at the boundary, and there is another state, the lowest-energy state, which is a constant: y 0 ( x) 1/ L Auroras Intensity Typical Aurora Emission Spectrum Species Present in the Atmosphere Constituents Contributing to Auroras + + O N O + 2 H 2 N O2