* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Altitudes, Medians, Bisectors of Triangles
Euler angles wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Perceived visual angle wikipedia , lookup
History of trigonometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
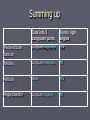
5.2 As we’re going through these slides, look for times when we can write equations: _______= _______ Introduction to Special Segments in Triangles & _______ = 90 Altitudes, Medians, & Bisectors of Triangles Perpendicular Bisector of A triangle: ►Bisects the side of the triangle & ►Makes a right angle. ►May or may not begin at a vertex _______= _______ (segments) & _______ = 90 (angle) Angle Bisector of A triangle: ►Bisects the angle it’s drawn from. ►Always from the vertex to the side opposite. _______= _______ (angles) m1 = m2 1 2 Altitude of A triangle: height of a triangle. ► Always forms a right angle with the side ► The it intersects starts at a vertex and intersects _______ = 90 the opposite side. (angle) ► May be inside, outside or on the triangle. ► Always Median of A triangle: ►Always from the vertex to the midpoint of the opposite side. ► Bisects the side opposite the vertex. _______= _______ (sides) You Try! ► Identify the following special segments in A the triangles. Median ____ Perpendicular Bisector ____ Altitude ____ Angle Bisector ____ X B C W E Y V D Z F Example: ► Find the value of the variable. 1) Given: 𝐶𝑋 is an altitude of ABC. A 2) Given: 𝐵𝑉 is a median of ABC. 2x - 4 V X (5x) 8y C B Think About It… ► In the picture 𝐴𝑊 is a perpendicular bisector of the base. Can you prove the two triangles are congruent? A Explain which postulate you used. If mC = 65 and CB=23. Find the following: mWAB = ____ CW = _____ 25 C 65 65 W 11.5 |----------------------------------| 23 B Summing up Cuts into 2 congruent parts Forms right angles Perpendicular bisector Congruent segments Yes Median Congruent segments No Altitude None Yes Angle bisector Congruent angles No