Download electric current

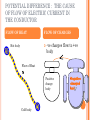
ELECTRIC CURRENT
ELECTRICITY
ELECTRIC
RESISTANCE
SERIES
CONNECTION
PARELLEL
CONNECTION
ELECTRIC
CURRENT
OHM’S LAW
ELECTRIC CURRENT
•The rate of flow of charge across any crosssection of a conductor is known as electric
current.
•It is a scalar quantity.
Direction Of Electronic Current -ve
to +ve ( flow of electrons)
Direction Of Conventional Current
+ve to –ve
I=Q/t
1 Ampere=1 Coulomb/ 1 second
When 1 coulomb of charge flows through any cross-section
of a conductor in 1 second, the electric current flowing through
it is said to be 1 ampere.
1 coulomb
1 ampere=
1 second
or
1C
1 A=
1s
Smaller units of current :
1
1 milliampere=
ampere
1000
1
1 mA=
A=103A
1000
1 A=106 A
Current is measured by an instrument called
ammeter.
An ammeter should have very low resistance.
Let the net charge be q flowing through the conductor, then
this charge q must carried by electrons through the conductor.
Assume that ‘n ‘ no. of electrons carry charge q, so we have
q = n*e ; e = fundamental electric charge = 1.6 × 10-19 C
n is the no. of electrons .
Hence we have I = (n*e) / t
For e.g : if 2A current is flowing through a conductor for 2 mins ,
calculate how many no. of e- ‘s must be flowing through it ?
soln : I = 2A ,
t = 2 min = 120 s
n=?
e = 1.6 × 10 -19 C
so we have, I = q /t ,  n*e / t
2 = (n * 1.6 × 10 -19 ) / 120
n = (2 * 120) / 1.6 × 10 -19
= 1.5 * 1021
POTENTIAL DIFFERENCE : THE CAUSE
OF FLOW OF ELECTRIC CURRENT IN
THE CONDUCTOR
FLOW OF HEAT
Hot body
FLOW OF CHARGES

-ve charges flow to +ve
body
Flow of Heat
Positive
charge
body
Cold body
EXPLANATION OF THE ACTIVITY.





A +ve body is always said to be at higher potential
and a –ve body is said to be at lower potential.
When we connect both bodies with a conducting wire,
as their is less concentrations of electrons in +ve body
, the electrons start flowing from –ve body to positive.
As the no. of electrons goes on increasing on +ve body
the potential keeps on decreasing and as the no. of
electrons keeps on decreasing on –ve body the
potential keeps on increasing.
The flow of electrons will continue till both potential
become same.
This difference of no. of electrons which existed in the
starting of this event , this difference is called
potential difference.
ELECTRIC POTENTIAL:
( THEORITICAL CONCEPT)
It is defined as the amount of work done to bring a unit
+ve charge from infinity to a given point against the
electric field.
 It is denoted by V .
 So if for unit charge if the work done is V, then for say
q amount of charge the work done will be qV.
 The difference in the potential for two points in the
circuit is called as potential difference.
 Its S.I unit is Volt (V).
 It is defined as if the 1 joule of work is done in carrying
1 coulomb of charge across two ends of the conductor,
the potential difference btn two ends will be 1 volt.

OHMS’S LAW:
Generally in all metallic conductors it is observed
that when the potential difference is maintained
between two terminals on the conductors and
current is allowed to flow through it.
 The ratio of the voltage and current remains
constant.
 Hence one can say that V ∞ I
V=RI
Where R = constant of proportionality or Resistance.
If we plot the graph of V  I , then we will get a
straight line passing through origin. And the slope
of the curve will be equal to R.

NON-OHMIC RESISTANCES
In some other electrical conductors like diode,
triode, electrolytes , they do not show ohmic
nature.
 Here the reason is that the devices are made in
such a way that they have varying resistances or
also called as dynamic resistances.
 They are so made due to cater the need for their
application, which requires change in resistances.
 If we plot the graph of V I for non-ohmic
resistances the graph is not a st. Line.

RESISTIVITY OF A CONDUCTOR
R ∞ L ( length of a conductor)

∞ A ( Area of cross-section of the conductor)
 By combining the above two, we have
 R = (SL) / A ;
 Where S = the proportionality constant, and is called
as resistivity of the conductor.
 It’s the property of the material to resist the flow of
the electric current.
 Its value varies from material to material. And it
doesn't depend on the dimensions of the material
 S = (RA)/ L
= Ω m2 / m = Ω m. Is the unit of resistivity.
The reciprocal of resistivity is conductivity.
It’s unit is (Ω m)-1

EMF
Electromotive force of a cell is defined as the
potential difference across the electrodes of the
open circuit. ( not connected)
 It’s a maximum potential difference a cell or a
battery can provide.
 for e.g. If we say that batteries used in torch are of
1.5 V, that means those batteries can give a
maximum of 1.5V. In reality it is a little less than
1.5V.
 Why is it less ?
 Ans: it is less because it has to overcome internal
resistance of the battery or cell. So some energy is
lost in doing so and hence what we get is little less
, which is called as terminal voltage.

TERMINAL VOLTAGE
It is defined as
EMF – POTENTIAL DROP OF THE CELL.
V = E – Ir ;
E = emf, r = internal resistance and I is the current
through the cell.
from above we can calculate the value of r as
r = (E –V ) / I
the value of r depends on the following points.
 the nature and concentration of electrolyte, more
concentrated electrolyte more is the resistance.
 More the distance between electrolyte more is the
internal resistance
 Amount of electrodes submerged in the electrolyte,
more submerged less is the resistance.
 More temperature of electrolyte less is the internal
resistance.

SERIES CONNECTIONS OF RESISTANCES


Consider three resistances R1, R2, &
R3 connected in series combination
with a power supply of voltage.
Potential difference of each resistor
is V1, V2, & V3 respectively. Let
electric current I is passing through
the circuit.
Now V = V1 + V2 + V3
According to Ohm’s law V = IR
thus :
IRe = IR1 + IR2 + IR3
Re = equivalent R in series.
IRe = I(R1 + R2 + R3)
IRe/I = R1 + R2 + R3

Re = R1 + R2 + R3
This shows that in series
combination equivalent resistance
of circuit is always greater than
individual resistances.
MORE ABOUT SERIES CONNECTION:
Characterstics
1. If different resistances are
joined with each other such
that there is only one path
for the flow of electric
current then the
combination of such
resistances is called Series
Combination.

2. In series combination
current through each
resistor is constant.
3. In series combination
Potential difference across
each resistor is different
depending upon the value
of resistance.
4. Equivalent resistance of
circuit is equal to the sum
of individual resistances.


Disadvantages
If one component is fused,
then the other components
of circuit will not function.
PARELLEL CONNECTION OF
RESISTANCES :

Consider three resistances
R1 , R2 & R3 connected in
parallel combination with
a power supply of voltage
V.
Now
I = I1 + I 2 + I3
According to Ohm’s law
V/R = I ; I1 = V/R1, similarly
for I2 , I3.
Therefore,
V/Re = V/R1 + V/R2 + V/R3
V/Re = V(1/R1 + 1/R2 + 1/R3)
V/Re*V = 1/R1 + 1/R2 + 1/R3
OR
MORE ABOUT PARALLEL CONNECTION :

Characteristics:
1. If there are more than
one path for the flow of
current in a circuit then the
combination of resistances
is called Parallel
Combination.
2. In parallel combination
current through each
resistor is different.
3. Potential difference
across each resistor is
constant.
4. Equivalent resistance of
circuit is always less than
either of the resistances
included in the circuit.


ADVANTAGE:
In parallel combination of
resistors, if one component of
circuit (resistor) is damaged
then rest of the component of
the circuit will perform their
work without any disturbance.
It is due to the presence of
more than paths for the flow
of electric current.