Download correlation coefficient

Last lecture summary
Confidnce interval
• confidence interval of the mean
• Confidence level 95%, what does it mean?
• How is the interval constructed?
𝑠
𝑚𝑒𝑎𝑛 ± 𝑠𝑜𝑚𝑒𝑡ℎ𝑖𝑛𝑔 ×
𝑛
– what is 𝑠𝑜𝑚𝑒𝑡ℎ𝑖𝑛𝑔?
– Z-value on the standard normal distribution
tn-1-value on t-distribution
Hypothesis testing
• We test a claim about what?
– population parameter
• Two hypothesis?
• Which hypothesis we test? What does it
mean statistically significant?
• So, how would you proceed in testing the
following claim: “Jarda sleeps on average
8 hours 45 minuts a day”?
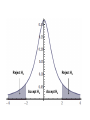
Reject Ho
Reject Ho
Accept Ho
Accept Ho
•
Set up the null and alternative hypotheses:
– Ho, says that the population parameter is equal to some claimed number.
– Three possible alternative hypotheses exist; choose the one that's most relevant.
• Ha: The population parameter is not equal (≠) to the claimed number.
• Ha: The population parameter is less than (<) the claimed number.
• Ha: The population parameter is greater than (>) the claimed number.
•
•
Take a random sample, calculate the sample statistic.
Convert the sample statistic to a test statistic:
– Take your sample statistic minus the number in the null hypothesis and divide by
the standard error of your statistic. This changes the distance to standard units.
•
Find the p-value for your test statistic.
– If Ha contains a less-than alternative, find the percentile in appropriate table (Z, t)
that corresponds to your test statistic.
– If Ha contains a greater-than alternative, find the percentile in appropriate table
(Z, t) that corresponds to your test statistic, and then take 100% minus that
percentile.
– Double this percentage if (and only if) Ha is the not-equal-to alternative.
– Change the percentage to a probability by dividing by 100, this is your p-value.
•
Examine your p-value and make your decision.
– Smaller p-values show more evidence against Ho. Reject the claim.
– Larger p-values show more evidence for Ho. Your sample supports the claim.
– Cutoff point (α level) between accpet/reject Ho, usually 0.05.
Errors in testing
• Type-1
– You reject Ho, while you shouldn’t.
– False positive
• Type-2
– You do not reject Ho, while you should.
– False negative
• The chance making a Type I error is α.
• The chance making a Type II error
depends mainly on the sample size.
– If you have more data, you’re less likely to
miss something that’s going on.
• However, large sample increases the
chance of Type I error.
• Type I and Type II errors sit on opposite
ends of a seesaw - as one goes up, the
other goes down.
• To try to meet in the middle, choose a
large sample size and a small α level (0.05
or less) for your hypothesis test.
New Stuff
Correlation and linear
regression
• Find a cricket, count the number of its
chirps in 15 seconds, add 37, you have
just approximated the outside temperature
in degrees Fahrenheit.
• National Service Weather Forecast Office:
http://www.srh.noaa.gov/epz/?n=wxcalc_cricketconvert
chirps in 15 sec temperature chirps in 15 sec temperature
18
57
27
68
20
60
30
71
21
64
34
74
23
65
39
77
• Each observation is composed of two
variables – bivariate data.
• First step in making sense of data is to
draw them – scatterplot.
• this is positive linear
relationship (proportional)
• opposite is negative linear
relationship (inverse)
We say that data are
correlated.
from Statistics for Dummies
• Looking at the scatterplot leads to the
conclusion that there appear to be a linear
positive relationship (as the chirps
increase, temperature increases).
• These two variables are associated.
• But you must be very careful if you want to
interpret the association as the causality.
• Look at the following example.
• There is a strong relationship
between the ice cream
consumption and the crime
rate.
• How could this be true?
• The two variables must have
something in common with one
another. It must be something
that relates to both level of ice
cream consumption and level
of crime rate. Can you guess
what that is?
• Outside temperature.
from causeweb.org
• If you stop selling ice cream, does the crime rate
drop? What do you think?
• That’s because of the simple principle that
correlations express the association that exists
between two or more variables; they have
nothing to do with causality.
• In other words, just because level of ice cream
consumption and crime rate increase/descrease
together does not mean that a change in one
necessarily results in a change in the other.
• You can’t interpret associations as being
causal.
• In ice cream example, there exist a
variable (outside temperature) we did not
realize to control.
• Such variable is called third variable,
confounding variable, lurking variable.
• The methodologies of scientific studies
therefore need to control for these factors
to avoid a type I error ('false positive‘)
conclusion that the dependent variables
are in a causal relationship with the
independent variable.
• Let’s have a look at dependence of murder
rate on temperature.
from http://www-personal.umich.edu/~bbushman/BWA05a.pdf
Journal of Personality and Social Psychology, 2005, Vol. 89, No. 1, 62–66
from http://www-personal.umich.edu/~bbushman/BWA05a.pdf
Journal of Personality and Social Psychology, 2005, Vol. 89, No. 1, 62–66
• Quantitative measure of correlation is a
correlation coefficient. It reflects the
amount of variability that is shared
between two variables and what they have
in common.
• It ranges between a value of –1 and a
value of +1.
• A correlation between two continuous
variables is described by the Pearson
correlation coefficient rxy
1 n  xi  x  yi  y 
rxy 

n  1 i 1
sx s y
n
s xy 
 x  x  y
i 1
i
n 1
i
 y
covariance
divide by n-1 for sample but by n for population
rxy 
sxy
sx s y
Covariance
• Watch explanation video.
http://www.youtube.com/watch?v=35NWFr53cgA
• Covariance and correlation are related
parameters that indicate the extent to
which two random variables co-vary.
• Covariance matrix is a matrix whose
element in the i, j position is the
covariance between the ith and jth elements
of a random vector.
Covariance matrix
elem1
elem2
3
5
2
4
4
6
random vector
with 2 elements
1. Standardize a data matrix A.
–
–
What does this mean?
Subtract mean, divide by standard
deviation. You get matrix B.
2. Covariance matrix is then
1
BT B
n 1
3 observations
of a random vector
elem1
elem2
0
0
-1
-1
1
1
–
What are the properties of
covariance matrix?
•
square, symmetric, positive definite,
real eigenvalues and eigenvectors
Back to the correlation coefficient
• The absolute value of the coefficient reflects
the strength of the correlation. So, a
correlation of –0.70 is stronger than a
correlation 0.50.
• One of the frequently made mistakes
regarding correlation coefficients occurs
when people assume that a direct or positive
correlation is always stronger (i.e., “better”)
than an indirect or negative correlation
because of the sign and nothing else.
•
•
•
•
•
.8 to 1.0
.6 to .8
.4 to .6
.2 to .4
.0 to .2
Very strong relationship
Strong relationship
Moderate relationship
Weak relationship
Weak or no relationship
However, there is a more
precise way to interpret
the correlation coefficient:
calculate the coefficient
of determination.
• Correlation matrix
income
education
attitude
vote
income education attitude
vote
1.00
0.35
-0.19
0.51
1.00
-0.21
0.43
1.00
0.55
1.00
Coefficient of determination
• Percentage of variance in one variable that is
accounted for by the variance in the other
variable.
• It is calculated simply as r2.
r2 = 0
r2 = 0.25
r2 = 0.81
from http://www.sagepub.com/upm-data/11894_Chapter_5.pdf
• Correlation analysis investigates the
relationships between variables using
graphs or correlation coefficients.
• Regression analysis answers the
questions like: which relationship exists
between variables X and Y (linear,
quadratic ,….), is it possible to predict Y
using X, and with what error?
Simple linear regression
• also single linear regression (jednoduchá lineární regrese)
• one y (dependent variable, závisle proměnná), one x
(independent variable, nezávisle proměnná)
• y^ = a + bx
• a – y-intercept (constant), b – slope
• y^ is estimated value, so to distinguish it from the actual
value y corresponding to the given x statisticans use y^
Data set
• Students in
higher grades
carry more
textbooks.
• Weight of the
textbooks
depends on the
weight of the
student.
Grade
Average Student
Wt. (lbs.)
Average Textbook
Wt. (lbs.)
1
48.50
8.00
2
54.50
9.44
3
61.25
10.08
4
69.00
11.81
5
74.50
12.28
6
85.00
13.61
7
89.00
15.13
8
99.00
15.47
9
112.00
17.36
10
123.00
18.07
11
134.00
20.79
12
142.00
16.06
strong positive correlation, r = 0.926
outlier
from Intermediate Statistics for Dummies
Build a model
• Find a straight line y = a + bx
from Intermediate Statistics for Dummies
• y-intercept (3.69 in our case)
– it may or may not have a practical meaning
• Does it fall within actual values in the data set? If yes, it is a clue it
may have a practical meaning.
• Does it fall within negative territory where negative y-value are not
possible? (e.g. weights can’t be negative)
• Does a value x = 0 have practical meaning (student weighting 0)?
– However, even if it has no meaning, it may be necessary
(i.e. significantly different from zero)!
• slope
– change in y due to one-unit increase in x (i.e. if student’s
weight increases by 1 pound, its textbook’s weight
increases by 0.113 pounds)
• now you can use regression line to estimate y value
for new x