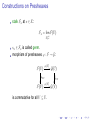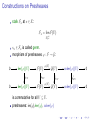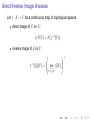Download Generalities About Sheaves - Lehrstuhl B für Mathematik

Generalities About Sheaves
Sebastian Jambor, Arne Lorenz
Lehrstuhl B für Mathematik
RWTH Aachen
summer school
Kleinwalsertal 2007
Outline
1
Presheaves
2
Sheaves
Examples
The Sheaf Associated to a Presheaf
Sequences and Cohomology
Sheaf Cohomology
3
Coherent Sheaves
Presheaves
Definition
Let X be a topological space. A presheaf F of abelian groups
consists of:
U ⊆ X open
abelian group of sections F(U ),
V ⊆ U open
restriction morphism
ρU V : F(U ) → F(V ),
such that:
F(∅) = 0,
ρU U = idF (U ) ,
W ⊆ V ⊆ U:
ρU W = ρV W ◦ ρU V .
For a section s ∈ F(U ) write s|V = ρU V (s).
Constructions on Presheaves
stalk Fx at x ∈ X:
Fx = lim F(U )
−→
U 3x
sx ∈ Fx is called germ.
Constructions on Presheaves
stalk Fx at x ∈ X:
Fx = lim F(U )
−→
U 3x
sx ∈ Fx is called germ.
morphism of presheaves ϕ : F → G:
F(U )
ϕ(U )
ρU V
F(V )
ϕ(V )
is commutative for all V ⊆ U .
/ G(U )
ρ0U V
/ G(V )
Constructions on Presheaves
stalk Fx at x ∈ X:
Fx = lim F(U )
−→
U 3x
sx ∈ Fx is called germ.
morphism of presheaves ϕ : F → G:
0
/ ker(ϕ)(U )
0
ρU V
/ ker(ϕ)(V )
/ F(U ) ϕ(U ) / G(U )
ρU V
/ F(V )
ϕ(V )
ρ0U V
/ G(V )
is commutative for all V ⊆ U .
presheaves: im(ϕ),ker(ϕ), coker(ϕ)
/ coker(ϕ)(U )
/0
ρ0U V
/ coker(ϕ)(V )
/0
Sheaves
Definition
Let {Vi } be an open covering of U ⊆ X (open). A presheaf F
on X is a sheaf if for all i:
s ∈ F(U ) and s|Vi = 0 then s = 0,
given si ∈ F(Vi ) that match on the overlaps:
si |Vi ∩Vj = sj |Vi ∩Vj
there is a unique s ∈ F(U ) with s|Vi = si .
Sheaves are defined by local data.
Examples of sheaves
X topological space: constant sheaves R, Z
(R, Z have discrete topology)
regular functions on an affine variety, e. g. An .
X ⊆ Rn : continuous functions C(U ) U → R
X ⊆ Rn : differentiable functions D(U ) U → R
X ⊆ Cn : holomorphic functions OX (U ) U → C
X ⊆ Cn : meromorphic functions
Extension to varieties, complex spaces and manifolds by gluing
is possible.
Types of sheaves
In the following, we deal with sheaves of
rings OX
ideals I with I(U ) E OX (U ),
OX -modules M.
(X, OX ) is called a ringed space with structure sheaf OX .
Module constructions extend to sheaves due to their local
nature:
⊕, F/G, ker, im, coker
Caution:
F/G, im, coker are only presheaves!
The sheaf associated to a presheaf
Every presheaf F defines a sheaf F + . For U ⊆ X take the
sections
[
s:U →
Fx
x∈U
such that:
s(x) ∈ Fx ,
for each x ∈ U we find:
x∈V ⊆U
and t ∈ F(V ) with tx = s(x).
The sheaf associated to a presheaf
Every presheaf F defines a sheaf F + . For U ⊆ X take the
sections
[
s:U →
Fx
x∈U
such that:
s(x) ∈ Fx ,
for each x ∈ U we find:
x∈V ⊆U
and t ∈ F(V ) with tx = s(x).
Equivalent definition of sheaves F + via ‘espaces étales’:
[
Fx
Spé(F) =
x∈X
F + (U ) are the continuous sections U → Spé(F).
Morphisms of sheaves
Use F + for some sheaves related to morphisms ϕ : F → G:
F 0 is a subsheaf of F if for each U ⊆ X:
0
F
F 0 (U ) ⊆ F(U ) and ρF
U V = ρU V |F (U )
Morphisms of sheaves
Use F + for some sheaves related to morphisms ϕ : F → G:
F 0 is a subsheaf of F if for each U ⊆ X:
0
F
F 0 (U ) ⊆ F(U ) and ρF
U V = ρU V |F (U )
ker(ϕ) is a subsheaf of F.
ϕ is injective ⇐⇒ ker(ϕ) = 0.
Morphisms of sheaves
Use F + for some sheaves related to morphisms ϕ : F → G:
F 0 is a subsheaf of F if for each U ⊆ X:
0
F
F 0 (U ) ⊆ F(U ) and ρF
U V = ρU V |F (U )
ker(ϕ) is a subsheaf of F.
ϕ is injective ⇐⇒ ker(ϕ) = 0.
The sheaf im(ϕ) is
im(ϕ) := impresheaf (ϕ)+
ϕ is surjective ⇐⇒ im(ϕ) = G.
Morphisms of sheaves
Use F + for some sheaves related to morphisms ϕ : F → G:
F 0 is a subsheaf of F if for each U ⊆ X:
0
F
F 0 (U ) ⊆ F(U ) and ρF
U V = ρU V |F (U )
ker(ϕ) is a subsheaf of F.
ϕ is injective ⇐⇒ ker(ϕ) = 0.
The sheaf im(ϕ) is
im(ϕ) := impresheaf (ϕ)+
ϕ is surjective ⇐⇒ im(ϕ) = G.
ϕ is surjective ⇐⇒
∀x ∈ X
ϕx : Fx → Gx
is surjective
but ϕ(U ) is not necessarily surjective.
Cohomology
Let (X, OX ) be a ringed space.
A sequence of sheaves:
S:
...
i−1
/ Si
/ S i−1 d
with im(di−1 ) ⊆ ker(di ).
S is exact ⇐⇒ im(di−1 ) = ker(di ).
di
i+1
/ S i+1 d
/ ...
Cohomology
Let (X, OX ) be a ringed space.
A sequence of sheaves:
S:
...
i−1
/ Si
/ S i−1 d
di
i+1
/ S i+1 d
/ ...
with im(di−1 ) ⊆ ker(di ).
S is exact ⇐⇒ im(di−1 ) = ker(di ).
S is exact ⇐⇒ the sequence of stalks is exact:
...
i−1
/ S i−1 dx / S i
x
x
dix
/ S i+1
x
/ ...
Cohomology sheaves:
hi (S) = (ker(di )/ im(di−1 ))+ .
∀x ∈ X.
Sheaf cohomology
Do not confuse this with the sheaf cohomology of F:
An injective resolution of F:
/F
0
/ S0
d0
/ S1
d1
/ ...
defines a sequence:
S:
0
/ S0
d0
/ S1
d1
/ S2
d2
/ ... .
The category of OX -modules has enough injectives.
Apply the global section functor Γ(X, ·) to S to obtain the
sheaf cohomology:
H q (X, F) = ker(dq (X))/ im(dq−1 (X))
H 0 (X, F) = Γ(X, F), since Γ(X, ·) is left exact.
Calculation: Next talks!
direct/inverse image sheaves
Let f : X → Y be a continuous map of topological spaces.
direct image of F on X:
f∗ F(V ) = F(f −1 (V ))
inverse image of G on Y :
+

f −1 (G)(U ) =  lim G(V )
−→
V ⊇f (U )
direct/inverse image sheaves
Let f : X → Y be a continuous map of topological spaces.
direct image of F on X:
f∗ F(V ) = F(f −1 (V ))
inverse image of G on Y :
+

f −1 (G)(U ) =  lim G(V )
−→
V ⊇f (U )
We can restrict sheaves F to subsets Z ⊆ X:
Z open: F|Z (V ) = F(V )
Z closed: Use the embedding ι : Z → X:
F|Z (V ) := ι−1 (F)(V )
Coherent sheaves
Definition
A sheaf F of OX -modules is coherent, if F is of finite type and
of relation finite type.
F is of finite type if for each x ∈ X there are x ∈ U ⊆ X,
p ∈ N and an exact sequence
p
OX
|U
σ
/ F|U
/ 0.
Coherent sheaves
Definition
A sheaf F of OX -modules is coherent, if F is of finite type and
of relation finite type.
F is of finite type if for each x ∈ X there are x ∈ U ⊆ X,
p ∈ N and an exact sequence
p
OX
|U
σ
/ F|U
/ 0.
F is of relation finite type if ker(σ) is of finite type.
Locally, a coherent sheaf has a finite representation:
q
OX
|U
/ O p |U
X
σ
/ F|U
/ 0.
Coherent sheaves II
The sheaf OX of holomorphic functions on a complex
space X is coherent.
The sheaf of differentiable functions D on a manifold X is
coherent.
For a coherent structure sheaf OX , an OX -module F is
coherent
⇐⇒ F locally has a finite representation.
Meromorphic functions do not form a coherent sheaf.
They are not finitely generated over OX .
Literature
Hans Grauert and Reinhold Remmert.
Coherent analytic sheaves, volume 265 of Grundlehren der
Mathematischen Wissenschaften.
Springer-Verlag, Berlin, 1984.
R. Hartshorne.
Algebraic geometry, volume 52 of Graduate Texts in
Mathematics.
Springer-Verlag, New York, 1977.
F. Hirzebruch.
Topological methods in algebraic geometry, volume 131 of
Grundlehren der Mathematischen Wissenschaften.
Springer-Verlag New York, Inc., New York, 1966.