* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 4-5 Isosceles and Equilateral Triangles
Multilateration wikipedia , lookup
Golden ratio wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Euler angles wikipedia , lookup
Noether's theorem wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Four color theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
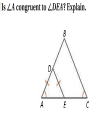
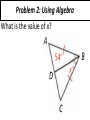
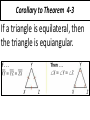
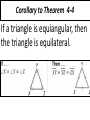
4-5 Isosceles and Equilateral Triangles • The congruent sides of an isosceles triangle are its legs • The third side is the base • The two congruent legs form the vertex angle • The other two angles are the base angles Isosceles Triangle Theorem If two sides of a triangle are congruent, then the angles opposite those sides are congruent Converse of the Isosceles Triangle Theorem If two angles of a triangle are congruent , then the sides opposite those angles are congruent Problem 1: Using the Isosceles Triangle Theorems Theorem 4-5 If a line bisects the vertex angle of an isosceles triangle, then the line is also the perpendicular bisector of the base Problem 2: Using Algebra What is the value of x? Corollary: is a theorem that can be proved easily using another theorem. A corollary is a theorem, so you can use it as a reason in a proof. Corollary to Theorem 4-3 If a triangle is equilateral, then the triangle is equiangular. Corollary to Theorem 4-4 If a triangle is equiangular, then the triangle is equilateral. Problem 3: Finding Angle Measures What are the measures of <A, <B, and <ADC in the photo?