Download Matched Pairs Samples - VCC Library

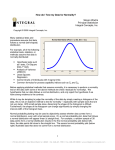
HOSP 1207 (Business Stats)
Learning Centre
Making Decisions with
Matched-Pairs Samples
Let’s say a manager of an accounting firm wants to evaluate the effects of a mandatory
ergonomics training program on reducing worker injuries. If the manager attempts to
compare a group of workers from her own firm who has had the training with a group of
workers from another firm who has not, she won’t be able to tell whether the training
program explains the difference in worker injuries. There are too many other factors that
could explain the difference! But, if the manager compares the number of worker
injuries from the same group of individuals before, and after, the training program, she
should be able to tell if the program is effective. This is an example of a matched-pairs
analysis.
Matched-pairs analysis is used for quantitative sets of data with normally distributed
differences. You are trying to make a decision about the average difference of the
population on the basis of the average difference of the sample. There can be two types
of studies:
1) matched-pairs experimental study – There is a measurement of some parameter,
followed by an action of some type, followed by a second measurement of the
same parameter in the same subjects or comparable subjects. Note that there
must be a clear correlation if two different groups of subjects are used (e.g.
people of a similar age, intelligence, and education if you’re testing whether the
graduates from one department earn more than graduates from another
department)
2) matched-pairs observational study – There is a matching or pairing of
observations, to help decide what caused an observed change between two
comparable groups.
For all matched pairs sets of data, the null hypothesis will be that the average
difference is 0. (H0: μD = 0) The three possible alternative hypotheses are: μD > 0, μD <
0, or μD ≠ 0. You will choose the alternative hypothesis based on the question of
interest and the order of the subtraction of the matched observations.
The first step will always be to calculate the differences. It is important to always be
consistent about the order of subtraction; if you are calculating for individual #1 the
difference in errors as “before” – “after”, you must follow the same rule for all other
individuals in your sample. You can’t swap to “after” – “before” part way through or your
data will be meaningless. You then must check that the differences are normally
distributed to ensure that the test is appropriate.
Next, find the sample mean of the differences and the standard deviation of the
differences using the same formulas from early in the course.
© 2013 Vancouver Community College Learning Centre.
Student review only. May not be reproduced for classes.
Authored by
by Emily
EmilySimpson
Simpson
Last, find the t-score for nD − 1 degrees of freedom and compare the t-score to the
critical t-value to decide whether to reject or fail to reject the null hypothesis.
Example 1: You want to study the effect of instituting a mandatory ergonomics training
program. You examine a random sample of people and observe the number of worker
injuries reported before and after their training. Use a significance level of 0.010. Note
that the last two columns will not be given with the data normally, they just show the
work for the solution.
Number of injuries
Worker Name Before
After
Angela
Darcy
Colin
Tyler
Robin
William
Phoebe
Hans
Maria
Alec
Javier
3
3
5
4
4
2
2
5
6
1
5
2
1
2
2
3
2
1
4
4
2
5
Difference Difference2
(xD)
(xD2)
1
1
2
4
3
9
2
4
1
1
0
0
1
1
1
1
2
4
-1
1
0
0
Solution: The first step is to calculate the differences in the number of injuries (shown
above as xD). Usually we want to try to set this up so the majority of the differences are
POSITIVE (in this case, before minus after). The null hypothesis is always μD = 0, and
the alternative hypothesis, H1 is: μD > 0 (since if the training is having an effect, the
number of injuries before training would be greater than the number of injuries after
training).
Since we don’t know anything about the normality of the population, we should check
for normality of the sample data by creating a histogram of the differences. Since the
histogram appears to be somewhat normal, we will assume that the population of
differences is normally distributed and calculate the t-score.
Sample size, nD is 11. We calculate the mean of the differences as the sum of all the
differences divided by the size of the sample:
∑
12
1.091
11
The standard deviation of the differences is
∑
∑
1.136
Since we don’t know anything about the normality of the population, we should check
for normality of the sample data by creating a histogram of the differences. Since the
© 2013 Vancouver Community College Learning Centre.
Student review only. May not be reproduced for classes.
2
histogram appears to be somewhat normal, we will assume that the population of
differences is normally distributed and calculate the t-score.
1.091
⁄√
0
1.136⁄√11
3.185
The critical t-value for 10 degrees of freedom and a significance level of 0.10 for a onetailed test is 2.764. Since our t-score is greater than the critical t-value, we reject the null
hypothesis. The training program has reduced the number of worker injuries.
Similarly to creating a confidence interval to estimate a population mean, we can do the
same thing to express an estimate of a population mean of differences.
·
√
For the example above, the confidence interval at 95% certainty would be 1.091 ± 0.763.
Exercises
1. An educational researcher believes that studying while listening to classical
music will improve a student’s retention of material. To try to prove her theory,
she devises a test where a random sample of students are given material to
review for 20 minutes and then tested on their recall. She records those results
and then repeats the process with a new test, but has the students listen to
classical music during the 20 minute review period. The test results are shown
below. Is there sufficient evidence at a 5% significance level to suggest that
playing classical music led to higher test scores?
Student Score (no
Score
music)
(music)
1
75
76
2
85
90
3
72
73
4
69
68
5
74
77
6
83
85
7
86
84
8
82
84
9
78
81
10
79
82
11
88
89
12
90
89
13
64
64
14
83
85
15
84
85
16
82
84
© 2013 Vancouver Community College Learning Centre.
Student review only. May not be reproduced for classes.
3
2. A small bake shop that specializes in gourmet cupcakes decides to rebrand itself.
The owner is certain that the new brand/logo will increase their sales Weekly
sales at a random sample of stores in Vancouver are recorded before and after
the company rebranding. Using a 2.5% level of significance, decide if the
rebranding has improved sales. Also construct a 95% confidence interval
estimate of the differences in sales after the company rebranding.
Weekly Sales Before and After Product Rebranding
Store
Sales after
Sales before
A
$837.42
$815.67
B
$826.54
$700.71
C
$817.86
$736.48
D
$871.97
$834.46
E
$771.44
$793.22
F
$788.19
$768.73
G
$725.17
$670.66
H
$571.95
$633.05
I
$753.87
$726.39
J
$731.04
$768.76
Solutions
1. Differences are normally distributed so we can proceed.
H0: μD = 0 H1: μD > 0 (calculate difference as with music – no music)
nD = 16, df = 15
1.375
1.7842
3.083
The critical t-value is 1.753. Since our calculated t-score is greater than the
critical t-value, this is a significant result. We reject H0 and conclude that listening
to classical music while studying does improve test scores.
2. H0: μD = 0 H1: μD > 0 (calculate difference as sales after – sales before)
nD = 10, df = 9
$24.73
$55.73
1.403
The critical t-value is 2.262. The t-score is less than the critical t-value so the
result is NOT significant. We fail to reject H0 and cannot conclude that the
rebranding has increased sales for the bake shop.
The confidence interval for the mean of differences at 95% confidence:
$ .
$24.73 2.262 ·
$24.73 $39.87
√
© 2013 Vancouver Community College Learning Centre.
Student review only. May not be reproduced for classes.
4