* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Propagation for Data Mining: Models, Algorithms and Applications
Human cytomegalovirus wikipedia , lookup
Middle East respiratory syndrome wikipedia , lookup
Ebola virus disease wikipedia , lookup
Orthohantavirus wikipedia , lookup
Marburg virus disease wikipedia , lookup
2015–16 Zika virus epidemic wikipedia , lookup
West Nile fever wikipedia , lookup
Hepatitis B wikipedia , lookup
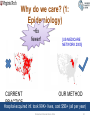
Influenza A virus wikipedia , lookup
Herpes simplex virus wikipedia , lookup
Leveraging Propagation for Data Mining Models, Algorithms & Applications B. Aditya Prakash Naren Ramakrishnan August 10, Tutorial, SIGKDD 2016, San About us • B. Aditya Prakash – Asst. Professor – CS, Virginia Tech. – PhD. CMU, 2012. – Data Mining, Applied ML • Graph and Time-series mining • Applications to Social Media, Epidemiology/Public Health, Cyber Security – Homepage: http://www.cs.vt.edu/~badityap/ Prakash and Ramakrishnan 2016 2 About us • Naren Ramakrishnan – Thomas L. Phillips Prof. – CS, Virginia Tech. – PhD. Purdue, 1997. – Data mining • for intelligence analysis, forecasting, sustainability, and health informatics – Homepage: http://people.cs.vt.edu/naren/ Prakash and Ramakrishnan 2016 3 Tutorial webpage • http://people.cs.vt.edu/~badityap/TALKS/16-kdd-tutorial/ • All Slides will be posted there. • Talk video as well (later). Prakash and Ramakrishnan 2016 4 Networks are everywhere! Facebook Network [2010] Gene Regulatory Network [Decourty 2008] Human Disease Network [Barabasi 2007] The Internet [2005] Prakash and Ramakrishnan 2016 5 Dynamical Processes over networks are also everywhere! Prakash and Ramakrishnan 2016 6 Why do we care? • • • • • • • • Social collaboration Information Diffusion Viral Marketing Epidemiology and Public Health Cyber Security Human mobility Games and Virtual Worlds Ecology • ........ Prakash and Ramakrishnan 2016 7 Why do we care? (1: Epidemiology) • Dynamical Processes over networks [AJPH 2007] Diseases over contact networks Prakash and Ramakrishnan 2016 CDC data: Visualization of the first 35 tuberculosis (TB) patients and their 1039 contacts 8 Why do we care? (1: Epidemiology) • Dynamical Processes over networks • Each circle is a hospital • ~3000 hospitals • More than 30,000 patients transferred [US-MEDICARE NETWORK 2005] Problem: Given k units of disinfectant, whom to immunize? Prakash and Ramakrishnan 2016 9 Why do we care? (1: Epidemiology) ~6x fewer! CURRENT PRACTICE [US-MEDICARE NETWORK 2005] OUR METHOD Hospital-acquired inf. took 99K+ lives, cost $5B+ (all per year) Prakash and Ramakrishnan 2016 10 Why do we care? (2: Online Diffusion) > 800m users, ~$1B revenue [WSJ 2010] ~100m active users > 50m users Prakash and Ramakrishnan 2016 11 Why do we care? (2: Online Diffusion) • Dynamical Processes over networks Buy Versace™! Followers Celebrity Social Media Marketing Prakash and Ramakrishnan 2016 12 Why do we care? (3: To change the world?) • Dynamical Processes over networks Social networks and Collaborative Action Prakash and Ramakrishnan 2016 13 High Impact – Multiple Settings epidemic outQ. How to squash rumors faster? breaks products/viruses Q. How do opinions spread? transmit s/w patches Q. How to market better? Prakash and Ramakrishnan 2016 14 Research Theme ANALYSIS Understanding POLICY/ ACTION DATA Large real-world networks & processes Managing Prakash and Ramakrishnan 2016 15 Research Theme – Public Health ANALYSIS Will an epidemic happen? DATA POLICY/ ACTION Modeling # patient transfers How to control out-breaks? Prakash and Ramakrishnan 2016 16 Research Theme – Social Media ANALYSIS # cascades in future? DATA POLICY/ ACTION Modeling Tweets spreading How to market better? Prakash and Ramakrishnan 2016 17 In this tutorial Given propagation models, on arbitrary networks: Q1: What is the epidemic threshold? Fundamental Models Understanding Q2: How do viruses compete? With extensions to dynamic networks, multiprofile networks etc. Prakash and Ramakrishnan 2016 18 In this tutorial Q3: How to estimate and learn influence and networks? Q4: How to immunize and control out-breaks better? Algorithms Managing/Manipula ting Q5: How to reverse-engineer epidemics? Q6: How to leverage viral marketing? Q7: How to pick sensors for graphs? Prakash and Ramakrishnan 2016 19 In this tutorial How to use propagation for _________ Q8: Memes, Tweets, Blogs Q9: Disease Surveillance Applications Q10: Protest Trends Large real-world networks & processes Q11: Malware Attacks Q12: General Graph Mining Prakash and Ramakrishnan 2016 20 Plan • Three breaks! – 2-2:05pm – 3-3:30pm (conference coffee break) – 4:15-4:20pm • Part 2: Algorithms starts at roughly 1:50pm • Part 3: Applications at 3:30pm (after the coffee break) • Please interrupt anytime for questions Prakash and Ramakrishnan 2016 21 Outline • Motivation • Part 1: Understanding Epidemics (Theory) • Part 2: Policy and Action (Algorithms) • Part 3: Applications (Data-Driven) • Conclusion Prakash and Ramakrishnan 2016 22 Part 1: Theory • Q1: What is the epidemic threshold? • Q2: How do viruses compete? Prakash and Ramakrishnan 2016 23 A fundamental question Strong Virus Epidemic? Prakash and Ramakrishnan 2016 24 example (static graph) Weak Virus Epidemic? Prakash and Ramakrishnan 2016 25 Problem Statement # Infected above (epidemic) below (extinction) Separate the regimes? time Find, a condition under which – virus will die out exponentially quickly – regardless of initial infection condition Prakash and Ramakrishnan 2016 26 Threshold (static version) Problem Statement • Given: –Graph G, and –Virus specs (attack prob. etc.) • Find: –A condition for virus extinction/invasion Prakash and Ramakrishnan 2016 27 Threshold: Why important? • • • • Accelerating simulations Forecasting (‘What-if’ scenarios Design of contagion and/or topology A great handle to manipulate the spreading – Immunization – Maximize collaboration ….. Prakash and Ramakrishnan 2016 28 Part 1: Theory • Q1: What is the epidemic threshold? – Background – Result and Intuition (Static Graphs) – Proof Ideas (Static Graphs) – Bonus: Dynamic Graphs • Q2: How do viruses compete? Prakash and Ramakrishnan 2016 29 “SIR” model: life immunity (mumps) • Each node in the graph is in one of three states – Susceptible (i.e. healthy) – Infected – Removed (i.e. can’t get infected again) Prob. δ t=1 t=2 Prakash and Ramakrishnan 2016 t=3 30 Terminology: continued • Other virus propagation models (“VPM”) – SIS : susceptible-infected-susceptible, flu-like – SIRS : temporary immunity, like pertussis – SEIR : mumps-like, with virus incubation (E = Exposed) ….…………. • Underlying contact-network – ‘who-can-infectwhom’ Prakash and Ramakrishnan 2016 31 Related Work R. M. Anderson and R. M. May. Infectious Diseases of Humans. Oxford University Press, 1991. A. Barrat, M. Barthélemy, and A. Vespignani. Dynamical Processes on Complex Networks. Cambridge University Press, 2010. F. M. Bass. A new product growth for model consumer durables. Management Science, 15(5):215–227, 1969. D. Chakrabarti, Y. Wang, C. Wang, J. Leskovec, and C. Faloutsos. Epidemic thresholds in real networks. ACM TISSEC, 10(4), 2008. D. Easley and J. Kleinberg. Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge University Press, 2010. A. Ganesh, L. Massoulie, and D. Towsley. The effect of network topology in spread of epidemics. IEEE INFOCOM, 2005. Y. Hayashi, M. Minoura, and J. Matsukubo. Recoverable prevalence in growing scale-free networks and the effective immunization. arXiv:cond-at/0305549 v2, Aug. 6 2003. H. W. Hethcote. The mathematics of infectious diseases. SIAM Review, 42, 2000. H. W. Hethcote and J. A. Yorke. Gonorrhea transmission dynamics and control. Springer Lecture Notes in Biomathematics, 46, 1984. J. O. Kephart and S. R. White. Directed-graph epidemiological models of computer viruses. IEEE Computer Society Symposium on Research in Security and Privacy, 1991. J. O. Kephart and S. R. White. Measuring and modeling computer virus prevalence. IEEE Computer Society Symposium on Research in Security and Privacy, 1993. R. Pastor-Santorras and A. Vespignani. Epidemic spreading in scale-free networks. Physical Review Letters 86, 14, 2001. All are about either: ……… ……… ……… • Static graphs Prakash and Ramakrishnan 2016 • Structured topologies (cliques, block-diagonals, hierarchies, random) • Specific virus propagation models 32 Part 1: Theory • Q1: What is the epidemic threshold? – Background – Result and Intuition (Static Graphs) – Proof Ideas (Static Graphs) – Bonus: Dynamic Graphs • Q2: How do viruses compete? Prakash and Ramakrishnan 2016 33 How should the answer look like? • Answer should depend on: – Graph – Virus Propagation Model (VPM) • But how?? – Graph – average degree? max. degree? diameter? – VPM – which parameters? – How to combine – linear? quadratic? exponential? 2 2 ( d avg davg ) / d max ? ….. d avg diameter ? Prakash and Ramakrishnan 2016 34 Static Graphs: Our Main Result • Informally, For, any arbitrary topology (adjacency matrix A) any virus propagation model (VPM) in standard literature • the epidemic threshold depends only 1. on the λ, first eigenvalue of A, and 2. some constant CVPM , determined by the virus propagation model In Prakash+ ICDM 2011 λ CVPM No epidemic if λ * CVPM < 1 35 Our thresholds for some models • s = effective strength • s < 1 : below threshold Models Effective Strength (s) s=λ. s=λ. SI1I2 V1 V2 (H.I.V.) s = λ . 1v2 2 v2 v1 SIS, SIR, SIRS, SEIR SIV, SEIV Threshold (tipping point) s=1 36 Our result: Intuition for λ “Official” definition: • Let A be the adjacency matrix. Then λ is the root with the largest magnitude of the characteristic polynomial of A [det(A – xI)]. “Un-official” Intuition • λ ~ # paths in the graph A k ≈ u k .u • Doesn’t give much intuition! A k (i, j) = # of paths i j of length k Prakash and Ramakrishnan 2016 37 Largest Eigenvalue (λ) better connectivity λ≈2 λ≈2 N = 1000 higher λ λ= N λ = N-1 λ= 31.67 λ= 999 Prakash and Ramakrishnan 2016 N nodes 38 Footprint Fraction of Infections Examples: Simulations – SIR (mumps) Time ticks (a) Infection profile Effective Strength (b) “Take-off” plot PORTLAND graph 31 million links, 6 million nodes 39 Footprint Fraction of Infections Examples: Simulations – SIRS (pertusis) Time ticks (a) Infection profile Effective Strength (b) “Take-off” plot PORTLAND graph 31 million links, 6 million nodes 40 Part 1: Theory • Q1: What is the epidemic threshold? – Background – Result and Intuition (Static Graphs) – Proof Ideas (Static Graphs) – Bonus: Dynamic Graphs • Q2: How do viruses compete? Prakash and Ramakrishnan 2016 41 Proof Sketch General VPM structure Model-based λ * CVPM < 1 Topology and stability Prakash and Ramakrishnan 2016 Graph-based 42 Models and more models Model Used for SIR Mumps SIS Flu SIRS Pertussis SEIR Chicken-pox …….. SICR Tuberculosis MSIR Measles SIV Sensor Stability SI1I2 V1 V2 H.I.V. ………. Prakash and Ramakrishnan 2016 43 Ingredient 1: Our generalized model Endogenous Transitions Susceptible Infected Exogenous Transitions Endogenous Transitions Vigilant Prakash and Ramakrishnan 2016 44 Special case: SIR Susceptible Infected Vigilant Prakash and Ramakrishnan 2016 45 Special case: H.I.V. SI1I2 V1 V2 “Non-terminal” “Terminal” Multiple Infectious, Vigilant states Prakash and Ramakrishnan 2016 46 Ingredient 2: NLDS + Stability • View as a NLDS – discrete time – non-linear dynamical system (NLDS) size mN x 1 . . . . . . Probability vector Specifies the state of the system at time t size N (number of nodes in the graph) Prakash and Ramakrishnan 2016 S I V 47 Ingredient 2: NLDS + Stability • View as a NLDS – discrete time – non-linear dynamical system (NLDS) size mN x 1 . . . . . . Non-linear function Explicitly gives the evolution of system Prakash and Ramakrishnan 2016 48 Ingredient 2: NLDS + Stability • View as a NLDS – discrete time – non-linear dynamical system (NLDS) • Threshold Stability of NLDS Prakash and Ramakrishnan 2016 49 Special case: SIR S size 3N x 1 S I I R R = probability that node i is not attacked by any of its infectious NLDS neighbors Prakash and Ramakrishnan 2016 50 Fixed Point 1 1 . 0 0 . 0 0 . State when no node is infected Q: Is it stable? Prakash and Ramakrishnan 2016 51 Stability for SIR Stable under threshold Unstable above threshold Prakash and Ramakrishnan 2016 52 See paper for full proof General VPM structure Model-based λ * CVPM < 1 Topology and stability Graph-based Prakash and Ramakrishnan 2016 53 Part 1: Theory • Q1: What is the epidemic threshold? – Background – Result and Intuition (Static Graphs) – Proof Ideas (Static Graphs) – Bonus: Dynamic Graphs • Q2: How do viruses compete? Prakash and Ramakrishnan 2016 54 Dynamic Graphs: Epidemic? Alternating behaviors DAY (e.g., work) adjacency matrix 8 8 Prakash and Ramakrishnan 2016 55 Dynamic Graphs: Epidemic? Alternating behaviors NIGHT (e.g., home) adjacency matrix 8 8 Prakash and Ramakrishnan 2016 56 Model Description Healthy • SIS model N2 – recovery rate δ N1 – infection rate β Infected Prob. β X Prob. δ N3 • Set of T arbitrary graphs day N night N N , weekend….. N Prakash and Ramakrishnan 2016 57 Our result: Dynamic Graphs Threshold • Informally, NO epidemic if eig (S) = Single number! Largest eigenvalue of The system matrix S In Prakash+, ECML-PKDD 2010 <1 S = 58 Infection-profile log(fraction infected) MIT Reality Mining Synthetic ABOVE ABOVE AT AT BELOW BELOW Time Prakash and Ramakrishnan 2016 59 Footprint (# infected @ “steady state”) “Take-off” plots Synthetic MIT Reality EPIDEMIC Our threshold NO EPIDEMIC Our threshold EPIDEMIC NO EPIDEMIC (log scale) Prakash and Ramakrishnan 2016 60 Extension: Multi-profile networks • Setting: – NOT fair play---same network, multiple profiles • • • • Example: PS4 tweet on Twitter network PS4 fans are positive People like brother may not care XBOX fans may be hostile – So, different βs and δs for different profiles In Rapti, Sioutas, Tsichlas, Tzimas SIGKDD 2015 Prakash and Ramakrishnan 2016 61 Extension: Multi-profile networks • Setting: – NOT fair play---same network, multiple profiles – Main results: • Situation much more complex • High sensitivity in one profile and low in another can still lead to epidemic Prakash and Ramakrishnan 2016 62 Part 1: Theory • Q1: What is the epidemic threshold? • Q2: What happens when viruses compete? – Mutually-exclusive viruses – Interacting viruses Prakash and Ramakrishnan 2016 63 Competing Contagions iPhone v Android Blu-ray v HD-DVD Attack v Retreat Biological common flu/avian flu, pneumococcal inf etc Prakash and Ramakrishnan 2016 64 A simple model • Modified flu-like • Mutual Immunity (“pick one of the two”) • Susceptible-Infected1-Infected2Susceptible Virus 2 Virus 1 Prakash and Ramakrishnan 2016 65 Question: What happens in the end? Number of Infections green: virus 1 red: virus 2 Footprint @ Steady State Footprint @ Steady State ASSUME: Virus 1 is stronger than Virus 2 = ? Prakash and Ramakrishnan 2016 66 Question: What happens in the end? Number of Infections green: virus 1 red: virus 2 Footprint @ Steady State Footprint @ Steady State ?? Strength Strength = 2 Strength Strength ASSUME: Virus 1 is stronger than Virus 2 Prakash and Ramakrishnan 2016 67 Answer: Winner-Takes-All Number of Infections green: virus 1 red: virus 2 ASSUME: Virus 1 is stronger than Virus 2 Prakash and Ramakrishnan 2016 68 Our Result: Winner-Takes-All Given our model, and any graph, the weaker virus always dies-out completely 1. The stronger survives only if it is above threshold 2. Virus 1 is stronger than Virus 2, if: strength(Virus 1) > strength(Virus 2) 3. Strength(Virus) = λ β / δ same as before! In Prakash+ WWW 2012 Prakash and Ramakrishnan 2016 69 Real Examples [Google Search Trends data] Reddit v Digg Blu-Ray v HD-DVD 70 Prakash and Ramakrishnan 2016 Part 1: Theory • Q1: What is the epidemic threshold? • Q2: What happens when viruses compete? – Mutually-exclusive viruses – Interacting viruses Prakash and Ramakrishnan 2016 71 A simple model: SI1|2S • Modified flu-like (SIS) • Susceptible-Infected1 or 2-Susceptible • Interaction Factor ε – Full Mutual Immunity: ε = 0 – Partial Mutual Immunity (competition): ε < 0 – Cooperation: ε > 0 Virus 1 & Virus 2 72 Prakash and Ramakrishnan 2016 Question: What happens in the end? ε=0 Winner takes all ε=1 Co-exist independently 0.8 0.7 0.6 0.5 0.4 0.3 0.2 k1 k2 0.1 0 0 100 200 300 400 Time 500 600 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 k1 k2 0.1 i1,2 0 700 800 Footprint (Fraction of Population) 0.9 Footprint (Fraction of Population) Footprint (Fraction of Population) 0.9 ε=2 Viruses cooperate 20 40 60 80 Time 100 120 0.8 0.7 0.6 0.5 0.4 0.3 0.2 k1 k2 0.1 i1,2 0 140 20 40 60 80 Time 100 120 What about for 0 < ε <1? Is there a point at which both viruses can co-exist? ASSUME: Prakash and Ramakrishnan 2016 Virus 1 is stronger than Virus 2 73 140 Footprint (Fraction of Population) Answer: Yes! There is a phase transition 0.8 0.6 0.4 0.2 k1 k2 0 0 100 200 300 400 Time 500 600 700 ASSUME: Virus 1 is stronger than Virus 2 Prakash and Ramakrishnan 2016 74 800 Footprint (Fraction of Population) Answer: Yes! There is a phase transition 0.8 0.6 0.4 0.2 k1 k2 0 i1,2 20 40 60 80 Time 100 120 140 ASSUME: Virus 1 is stronger than Virus 2 Prakash and Ramakrishnan 2016 75 Footprint (Fraction of Population) Answer: Yes! There is a phase transition 0.8 0.6 0.4 0.2 k1 k2 0 i1,2 0 50 100 150 Time 200 250 ASSUME: Virus 1 is stronger than Virus 2 Prakash and Ramakrishnan 2016 76 300 Our Result: Viruses can Coexist Given our model and a fully connected graph, there exists an εcritical such that for ε ≥ εcritical, there is a fixed point where both viruses survive. 1. The stronger survives only if it is above threshold 2. Virus 1 is stronger than Virus 2, if: strength(Virus 1) > strength(Virus 2) 3. Strength(Virus) σ = N β / δ In Beutel+ SIGKDD 2012 77 Real Examples [Google Search Trends data] Hulu v Blockbuster Prakash and Ramakrishnan 2016 78 Real Examples [Google Search Trends data] Chrome v Firefox Prakash and Ramakrishnan 2016 79 We can also extend this to • Composite networks [Wei+ JSAC 2013] – phone call + SMS networks – power grid + telecomm networks • Main result: Behavior depends on viral strengths in the different networks – Also depends on strength of interaction between the networks Prakash and Ramakrishnan 2016 80