Download 9-5 Inscribed Angles

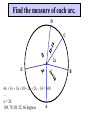
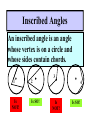
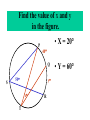
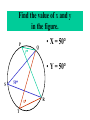
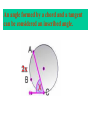
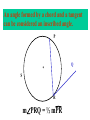
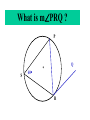
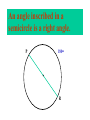
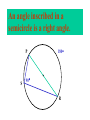
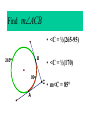
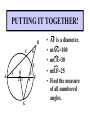
8-5 Angles in Circles
Central Angles
• A central angle is an angle whose vertex is
the CENTER of the circle
Central
Angle
(of a circle)
Central
Angle
(of a circle)
NOT A
Central
Angle
(of a circle)
CENTRAL ANGLES AND ARCS
The measure of a central angle is equal to
the measure of the intercepted arc.
CENTRAL ANGLES AND ARCS
The measure of a central angle is equal to
the measure of the intercepted arc.
Central
Y
Angle
O
110
Z
Intercepted Arc
EXAMPLE
• Segment AD is a diameter. Find the
values of x and y and z in the figure.
25
B
C
A
x y
z
55
O
D
x = 25°
y = 100°
z = 55°
SUM OF CENTRAL ANGLES
The sum of the measures fo the central angles of a circle with
no interior points in common is 360º.
360º
Find the measure of each arc.
D
C
2x
E
4x + 3x + 3x + 10+ 2x + 2x – 14 = 360
…
x = 26
A
104, 78, 88, 52, 66 degrees
B
Inscribed Angles
An inscribed angle is an angle
whose vertex is on a circle and
whose sides contain chords.
1
Is
NOT!
2
Is SO!
3
4
Is
NOT!
Is SO!
Thrm 9-7. The measure of an inscribed angle is
INSCRIBED
ANGLE
THEOREM
equal to ½ the measure
of the intercepted
arc.
The measure of an inscribed angle is equal
to ½ the measure of the intercepted arc.
x
1
x
2
Thrm 9-7. The measure of an inscribed angle is
INSCRIBED
ANGLE
THEOREM
equal to ½ the measure
of the intercepted
arc.
The measure of an inscribed angle is equal
to ½ the measure of the intercepted arc.
1

2
Thrm 9-7. The measure of an inscribed angle is
INSCRIBED
ANGLE
THEOREM
equal to ½ the measure
of the intercepted
arc.
The measure of an inscribed angle is equal
to ½ the measure of the intercepted arc.
Inscribed Angle
Y
55
Z
Intercepted Arc
Thrm 9-7.
Thethe
measure
of anofinscribed
Find
value
x andangle
y is
equal to ½ the measure of the intercepted arc.
in the figure.
• X = 20°
P
40
Q
S
50
y
x
T
R
• Y = 60°
Corollary
1. Ifthe
two inscribed
angles
intercept
Find
value of
x and
y the
same arc, then the angles are congruent..
in the figure.
• X = 50°
P
y
Q
• Y = 50°
S
50
x
T
R
An angle formed by a chord and a tangent
can be considered an inscribed angle.
An angle formed by a chord and a tangent
can be considered an inscribed angle.
P
Q
S
R
mPRQ = ½ mPR
What is mPRQ ?
P
Q
S
60
R
An angle inscribed in a
semicircle is a right angle.
P
180
R
An angle inscribed in a
semicircle is a right angle.
P
S
180
90
R
Interior Angles
• Angles that are formed by two
intersecting chords. (Vertex IN the
circle)
A
D
B
C
Interior Angle Theorem
The measure of the angle formed by the
two chords is equal to ½ the sum of the
measures of the intercepted arcs.
Interior Angle Theorem
The measure of the angle formed by the
two chords is equal to ½ the sum of the
measures of the intercepted arcs.
A
D
1
B
C
1
m1  (mAC  mBD)
2
Interior Angle Theorem
A
91
C
y°
x°
B
D
85
1
x  (91  85)
2
x  88
y  180  88
y  92
Exterior Angles
• An angle formed by two secants, two
tangents, or a secant and a tangent drawn
from a point outside the circle. (vertex
OUT of the circle.)
Exterior Angles
• An angle formed by two secants, two
tangents, or a secant and a tangent drawn
from a point outside the circle.
k
j 1
k
j 1
k
j
1
Exterior Angle Theorem
• The measure of the angle formed is equal
to ½ the difference of the intercepted
arcs.
k
j
1
k
j
1
1
m1  (k  j)
2
k
j
3
Find mACB
• <C = ½(265-95)
B
265
95
A
• <C = ½(170)
C
• m<C = 85°
PUTTING IT TOGETHER!
D
C
6
E
A
3
Q
2 1
5
4 F
G
•
•
•
•
•
AF is a diameter.
mAG=100
mCE=30
mEF=25
Find the measure
of all numbered
angles.
Inscribed Quadrilaterals
• If a quadrilateral is inscribed in a circle,
then the opposite angles are supplementary.
P
Q
mPSR + mPQR = 180 
S
R