* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 9-5 Inscribed Angles
Survey
Document related concepts
Transcript
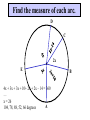
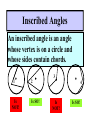
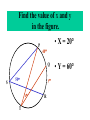
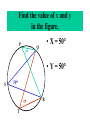
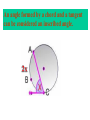
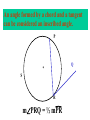
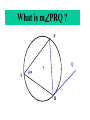
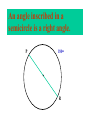
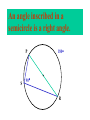
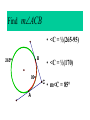
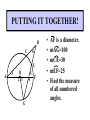
8-5 Angles in Circles Central Angles • A central angle is an angle whose vertex is the CENTER of the circle Central Angle (of a circle) Central Angle (of a circle) NOT A Central Angle (of a circle) CENTRAL ANGLES AND ARCS The measure of a central angle is equal to the measure of the intercepted arc. CENTRAL ANGLES AND ARCS The measure of a central angle is equal to the measure of the intercepted arc. Central Y Angle O 110 Z Intercepted Arc EXAMPLE • Segment AD is a diameter. Find the values of x and y and z in the figure. 25 B C A x y z 55 O D x = 25° y = 100° z = 55° SUM OF CENTRAL ANGLES The sum of the measures fo the central angles of a circle with no interior points in common is 360º. 360º Find the measure of each arc. D C 2x E 4x + 3x + 3x + 10+ 2x + 2x – 14 = 360 … x = 26 A 104, 78, 88, 52, 66 degrees B Inscribed Angles An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords. 1 Is NOT! 2 Is SO! 3 4 Is NOT! Is SO! Thrm 9-7. The measure of an inscribed angle is INSCRIBED ANGLE THEOREM equal to ½ the measure of the intercepted arc. The measure of an inscribed angle is equal to ½ the measure of the intercepted arc. x 1 x 2 Thrm 9-7. The measure of an inscribed angle is INSCRIBED ANGLE THEOREM equal to ½ the measure of the intercepted arc. The measure of an inscribed angle is equal to ½ the measure of the intercepted arc. 1 2 Thrm 9-7. The measure of an inscribed angle is INSCRIBED ANGLE THEOREM equal to ½ the measure of the intercepted arc. The measure of an inscribed angle is equal to ½ the measure of the intercepted arc. Inscribed Angle Y 55 Z Intercepted Arc Thrm 9-7. Thethe measure of anofinscribed Find value x andangle y is equal to ½ the measure of the intercepted arc. in the figure. • X = 20° P 40 Q S 50 y x T R • Y = 60° Corollary 1. Ifthe two inscribed angles intercept Find value of x and y the same arc, then the angles are congruent.. in the figure. • X = 50° P y Q • Y = 50° S 50 x T R An angle formed by a chord and a tangent can be considered an inscribed angle. An angle formed by a chord and a tangent can be considered an inscribed angle. P Q S R mPRQ = ½ mPR What is mPRQ ? P Q S 60 R An angle inscribed in a semicircle is a right angle. P 180 R An angle inscribed in a semicircle is a right angle. P S 180 90 R Interior Angles • Angles that are formed by two intersecting chords. (Vertex IN the circle) A D B C Interior Angle Theorem The measure of the angle formed by the two chords is equal to ½ the sum of the measures of the intercepted arcs. Interior Angle Theorem The measure of the angle formed by the two chords is equal to ½ the sum of the measures of the intercepted arcs. A D 1 B C 1 m1 (mAC mBD) 2 Interior Angle Theorem A 91 C y° x° B D 85 1 x (91 85) 2 x 88 y 180 88 y 92 Exterior Angles • An angle formed by two secants, two tangents, or a secant and a tangent drawn from a point outside the circle. (vertex OUT of the circle.) Exterior Angles • An angle formed by two secants, two tangents, or a secant and a tangent drawn from a point outside the circle. k j 1 k j 1 k j 1 Exterior Angle Theorem • The measure of the angle formed is equal to ½ the difference of the intercepted arcs. k j 1 k j 1 1 m1 (k j) 2 k j 3 Find mACB • <C = ½(265-95) B 265 95 A • <C = ½(170) C • m<C = 85° PUTTING IT TOGETHER! D C 6 E A 3 Q 2 1 5 4 F G • • • • • AF is a diameter. mAG=100 mCE=30 mEF=25 Find the measure of all numbered angles. Inscribed Quadrilaterals • If a quadrilateral is inscribed in a circle, then the opposite angles are supplementary. P Q mPSR + mPQR = 180 S R