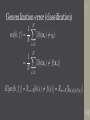Download Defining Learning

1/17/17
Machine Learning
Defining Learning
1
•
1/17/17
Types of learning
Supervised: we know input and targets
– Goal is to learn a model that, given input data,
accurately predicts target data
•
Unsupervised: we know the input only and want
to make generalizations
2
•
1/17/17
Supervised learning: Classification
Map inputs x to outputs y where 𝑦 ∈ {1, … , 𝐶}
where C is the number of classes
– Binary classification is C = 2
– Multinomial classification C > 2
– Multi-label classification: classes are not mutually
exclusive
•
Probabilistic interpretation: instead of returning
class assignment, return probability (certainty)
of class label.
3
•
Let ℎ 𝐱 + = Pr(𝑦+ |𝐱 + , 𝒟, ℋ)
•
ℎ(𝐱 + ) is a vector of length c, indicating how likely
each class c is.
•
Our best guess of the particular class assignment
for any x is
𝑦4 = 𝑔 𝐱 = argmax Pr(𝑦 = 𝑐|𝐱, 𝒟, ℋ)
1/17/17
Probability and Classification
:;<
This is considered the MAP (maximum a
posteriori) estimate
•
Clearly, ℎ(𝐱 + ) has more information than just 𝑦4
4
•
Classification except we now have continuous
response variables.
•
𝑥 ∈ ℝ@ , 𝑦 ∈ ℝ< , estimate a function 𝑔 𝐱 = 𝑦4 such
that 𝑦4 ≈ 𝑓 𝑥 + 𝜖
1/17/17
Supervised learning: Regression
5
1/17/17
Probability and Regression
•
Let ℎ 𝐱 + = Pr(𝑦+ |𝐱 + , 𝒟, ℋ)
•
In linear regression ℎ 𝐱 + = 𝐰 G 𝐱 + which returns
estimate 𝑦4.
•
Our best guess for ℎ 𝐱 + = 𝐰 G 𝐱 +
N
𝑦4 = 𝑔 𝐱 = argm𝑖𝑛 K 𝑦+ − 𝐰 G 𝐱 +
J
M
+;<
This is considered the MLE (maximum
likelihood) estimate
6
1/17/17
What are some supervised learning
questions that are classification and
regression problems?
7
•
Estimate which cluster each data point belongs
to by looking for patterns in the input data.
•
Let K denote the number of clusters.
•
We need to infer the distribution over the
number of clusters or Pr 𝐾 𝓓 .
•
Usually we assume 𝐾 ∗ = argmax Pr(𝐾|𝓓) then
1/17/17
Unsupervised learning: Clustering
S
we need to estimate the class of each data point.
𝑧+∗ = argmax 𝐏𝐫(𝑧+ = 𝑘|𝐱 + , 𝓓, ℎ(𝐱)
U
8
•
In unsupervised learning we often use high
dimensional data (e.g. images, text)
•
We often consider dimensionality reduction as a
means to capture the “essence” of the data
1/17/17
Unsupervised learning: Latent
Factors
– What features are meaningful for distinguishing among
images or documents
– Can we discover a low dimensional space capable of
explaining the data nearly as well
9
•
1/17/17
Other types of Unsupervised learning
Discovering graph/relational structure
– Graphical Models
– Network analysis
•
Matrix completion
– Image imputation (fill in holes/occlusions of images)
– Collaborative filtering (movie prediction example)
– Market basket analysis (collaborative filtering with no
missing data)
10
1/17/17
What are some unsupervised learning
questions that are cluster detection or
latent factor discovery?
11
Supervised vs. Unsupervised
methods
•
Supervised:
There exists a ground truth
•
Find patterns
in fully observed data
•
Then predict on partially observed data.
•
Collection of emails spam/not spam
•
After learning about the difference, categorize
new incoming messages
Supervised vs. Unsupervised
methods
•
Unsupervised:
find hidden/latent structure in
data
•
Patterns are not formally
observed
•
Difficult to evaluate accuracy
of unsupervised models
•
But are useful in tackling problems such as
image classification, speech processing and
semantic topics
Discrete vs. Continuous methods
•
Discrete: manipulate a countable set of objects
– classification, count
•
Continuous: methods manipulating continuous
values
– stock market prediction, regression problems
The space of models
supervised
unsupervised
discrete
classification
clustering
continuous
regression
dimensionality
reduction
The space of models
supervised
unsupervised
discrete
classification
clustering
continuous
regression
dimensionality
reduction
predictions: an individual’s job, main object in an image, event
models: logistic regression, neural network classification, SVM
The space of models
supervised
unsupervised
discrete
classification
clustering
continuous
regression
dimensionality
reduction
data: topic of a newspaper article, similarity
models: k-means, topic modeling
The space of models
supervised
unsupervised
discrete
classification
clustering
continuous
regression
dimensionality
reduction
predictions: income, number of papers published
models: linear regression, regression trees
The space of models
supervised
unsupervised
discrete
classification
clustering
continuous
regression
dimensionality
reduction
data: NLP, dynamical systems
models: kernel methods, process models, Bayesian non-parametric
20
1/17/17
1/17/17
Machine Learning
Defining What Learning isn’t
21
•
We’ve discussed a bit about learning from data
•
But some approaches don’t use data….
•
Or use data in a different way.
1/17/17
Learning vs Design
22
•
1/17/17
Coin recognizer: Data solution
ML approach: Measure size and mass of coins,
find hypothesis that explains data well.
23
•
Call the mint, ask for information about the size
of the coins and variability around the size. Ask
for frequency of production of each coin.
•
Physically model variation in size and mass
1/17/17
Coin recognizer: Design solution
– Consider wear and tear on the coins.
– Measurement error of the system.
24
•
Data confirms relationships between input and
output (e.g. force = mass times acceleration).
•
This doesn’t use data to build the model, just
confirm the functional form.
1/17/17
High School Physics
25
•
ML is the intersection of a learning algorithm and a
hypothesis set
•
If my hypothesis set is very constrained, ML
algorithms won’t work.
1/17/17
Theory Driven vs Data Driven
– Theoretical constraints on the hypothesis space.
– A solution exists, but it’s not in any common hypothesis set.
•
It often is the case we have additional (theoretical)
assumptions that constrain our hypothesis space.
•
If we can write down an analytical (theoretic) form, no
point in using data driven solutions.
26
27
1/17/17
•
There must be a pattern in the data.
•
We cannot pin down the pattern mathematically.
1/17/17
Requirements of learning
– Instead we’re looking at generalization of a theory
•
We have data.
•
Supervised learning assumption for this lecture.
g ⇡ f.
– Unknown target function
– Data D
– Learning algorithm picks g ⇡ f from the hypothesis set H
28
•
1/17/17
Requirements of learning…
What if we don’t have a pattern?
– Our model just doesn’t learn
•
What if there’s a mathematical form?
– We can still try ML but it isn’t the right tool. The
analytic solution will almost surely be better.
•
What if we don’t have data…
– We’re out of luck. We absolutely need data.
29
•
Intuition says we need data for training.
•
More fundamentally, learning requires data.
•
Two tasks:
1/17/17
Why do we need data?
– Learn the data that is observed (consistency)
– Approximate the underlying target function f such that
we can predict to unseen data (generalization)
30
•
1/17/17
Finding a good model
How do we know what our hypothesis set
ℋshould be?
– In our previous example, we assumed any linear model.
•
In practice this is specific to the domain and the
amount of data available.
– The larger and more complex our hypothesis set ℋ is,
the more data we need.
– The closer (or more confident) we want to be in our
predictions, the more data we need.
31
•
1/17/17
Over vs underfitting
If our hypothesis set is large or our model is
complex, our model is more capable of accounting
for the observed training data.
– This includes capturing the noise and error (or
variance) of these data.
•
If our hypothesis set is too simplistic (e.g. linear
model for a quadratic system) or our model too
simple, we cannot account for the observed
training data perfectly.
– In fact our estimates will be biased.
32
•
In Machine learning, we always have training
data
•
But the goal is to have good performance on
unseen data.
•
How do we estimate performance on unseen
data?
1/17/17
Training vs Testing
– Pull out some of the training data and use as a testing
set.
– Testing data should only be used on a fully trained
model (more soon)
33
Interpretability vs. Flexibility
interpretability
Linear model
Neural networks
flexibility
interpretability
Interpretability vs. Flexibility
Strong assumptions about
relationship between
X and Y
Few assumptions about
relationship, once
relationship is uncovered,
difficult to interpret
flexibility
interpretability
Interpretability vs. Flexibility
≈ # of parameters
flexibility
The basics of model evaluation
•
We train a model on observations where we know both
X and Y.
•
We test our model by asking, given X, what do we
expect Y to be.
•
To understand how our mode performs we look at the
difference between our expected Y and our observed Y
on the test set.
•
Error is computed as a cost function based on the
difference between estimated Y and true Y.
•
Can we know anything about model selection and
learning before we start?
•
E.g. Is learning feasible?
•
There’s a whole literature on this
(statistical/computational learning theory) that
we won’t cover here.
1/17/17
General model performance
38
1/17/17
Can we learn?
39
•
1/17/17
Can we learn?
It’s unclear that we can always learn.
– A particular input may have an output that is outside of
anything our training data would allow us to expect
•
But usually we can do something.
– Our sample data x is related to the sample space X
– If we learn a probability distribution underlying X, we
can make more informed estimates
•
That’s learning!
40
•
1/17/17
Probability distributions
Next class.
41
•
Before even talking about the specifics of a
model, I know some things about performance
expectations.
•
This comes mostly from statistics but we’ll
review it here.
1/17/17
Performance breakdown
42
Evaluating model accuracy
2.1estimated
What Is Statistical
19
How good of a model is our
model atLearning?
actually approximating f ?
manufacturing variation in the drug itself or the patient’s general feeling
• Two types of error
of well-being on that day.
– reducible: we can build
better and better models to close
ˆ
Consider the
a given
estimate
andmodel
a set and
of predictors
X,are
which yields the
gap between
thef true
the model we
estimate
prediction Ŷusing
= fˆto
(X).
Assume for a moment that both fˆ and X are fixed.
( ε )that
Then, it is– irreducible
easy to show
•
E(Y − Ŷ )2
=
=
E[f (X) + ϵ − fˆ(X)]2
[f (X) − fˆ(X)]2 + Var(ϵ) ,
! "# $
!
"#
$
Reducible
ˆ
2
Irreducible
(2.3)
Model fit
31
1.5
1.0
0.0
2
4
0.5
6
Y
8
Mean Squared Error
10
2.0
12
2.5
2.2 Assessing Model Accuracy
0
20
40
60
X
80
100
2
5
10
20
Flexibility
FIGURE 2.9. Left: Data simulated from f , shown in black. Three estimates of
f are shown: the linear regression line (orange curve), and two smoothing spline
fits (blue and green curves). Right: Training MSE (grey curve), test MSE (red
Model fit
33
1.5
1.0
0.0
2
4
0.5
6
Y
8
Mean Squared Error
10
2.0
12
2.5
2.2 Assessing Model Accuracy
0
20
40
60
X
80
100
2
5
10
20
Flexibility
FIGURE 2.10. Details are as in Figure 2.9, using a different true f that is
much closer to linear. In this setting, linear regression provides a very good fit to
the data.
Model fit
2. Statistical Learning
15
10
5
0
−10
0
Y
10
Mean Squared Error
20
20
34
0
20
40
60
X
80
100
2
5
10
20
Flexibility
FIGURE 2.11. Details are as in Figure 2.9, using a different f that is far from
linear. In this setting, linear regression provides a very poor fit to the data.
Testing vs training error
X
80
100
02
20
5 40
1060
X
Flexibility
80
20
100
20
15
10
5
0
−10
0.0
Mean Squared Error
Y
Mean Squared Error
0
10
20
0.5
1.0
1.5
2.0
81.5
6
1.0
0.02
60
33
2.5
10 2.0 12 2.5
31 2.22.Assessing
Model
Accuracy
34
Statistical
Learning
4
0.5
Y
Mean Squared
Error
2.2 Assessing Model Accuracy
0 2
20
5
40
10
60
Flexibility
X
8020
100
2
5
10
20
Flexibility
FIGURE
Details
areestimates
as in Figure
different
that is2.9, using a different f that is far from
FIGURE
2.11.aDetails
aretrue
as inf Figure
Data simulated from
f , shown2.10.
in black.
Three
of 2.9, using
much closer
to and
linear.
this setting,
linear
provides
a very
good fit provides
to
linear.regression
In this setting,
linear
regression
a very poor fit to the data.
regression line (orange
curve),
twoInsmoothing
spline
the data.
rves). Right: Training
MSE (grey curve), test MSE (red
Bias-Variance trade-off
•
E[(Y
All error can be broken down into three parts.
2
Ŷ ) ] = E[f (X) + ✏
h(X)]
2
2
= V ar(h(X)) + (Bias(h(X))) + V ar(✏)
•
We define bias as 𝐸Z([) ℎ 𝑋 − 𝑓 𝑋
•
With expected value methods and basic
assumptions about 𝜖, we can prove this (hint:
this may be on the midterm)
Intuition: Variance of 𝑓
•
How much would our estimated 𝑓 change if we
estimated it using different training data?
•
If we removed a point, how much
would our estimate change?
•
If we reran our data collection, we’d
get different observations. Would
that change the fit of the green line?
of the yellow line?
2. Statistical Learning
15
10
5
0
−10
0
Y
10
Mean Squared Error
20
20
34
0
20
40
60
80
100
2
X
FIGURE 2.11. Details are as in Figure 2.9, using a di
Intuition: Bias of 𝑓
Introduced by the assumption of our estimated ℎ(𝑥)
ℎ 𝑋 −𝑓 𝑋
•
Bias cannot be reduced by more
training data but only by a more
complex model.
20
20
0
0
−10
15
For example, linear regression assumes
linear relationship. Probably not entirely
true so our estimated outcomes are
biased.
2. Statistical Learning
10
•
34
5
Expected difference between true f and
our hypothesis.
Mean Squared Error
•
10
• 𝐸Z([)
Y
•
0
20
40
60
X
80
100
2
Bias-Variance tradeoff
•
We want simple interpretable models
•
But with simple models comes biases (e.g.
assumptions of linearity)
•
As we increase flexibility, we decrease bias.
•
The cost of flexibility though is increased
variance.
20
15
2.0
MSE
Bias
Var
0.5
2
5
10
Flexibility
20
0
0.0
0.0
0.5
5
1.0
1.0
10
1.5
1.5
2.0
2.5
2. Statistical Learning
2.5
36
2
5
10
Flexibility
20
2
5
10
20
Flexibility
FIGURE 2.12. Squared bias (blue curve), variance (orange curve), Var(ϵ)
•
All of this shows us the relationship between the
hypothesis set, a given ℎ 𝑋 and the true
(unknown) function 𝑓 𝑋
•
But how to do we evaluate and choose the
specific hypothesis set and then a specific 𝑔 𝑋
given ℋ, 𝒟|𝑓?
•
Remember 𝑓 is UNKNOWN.
•
Usually, our hypothesis set ℋ is a choice of
model flexibility (e.g. neural networks vs linear
models)
1/17/17
Model vs hypothesis evaluation
52
•
1/17/17
Model Evaluation
We want to pick the best hypothesis 𝑔 ∈ ℋ such
that 𝑔 ≈ 𝑓 to the best of our ability.
– How do we assess the fit of 𝑔 to the true function 𝑓
when 𝑓 is unknown?
•
We want a function that is consistent (stats
cares, ML not so much)
– Altering the parameters slightly doesn’t dramatically
change the result
•
More importantly, we want a function that
generalizes (focus of ML)
– Good estimates for input values that haven’t been seen
during training.
53
1/17/17
Generalization error (classification)
N
X
1
err(h, f ) =
I(h(xi ) 6= yi )
N i=1
N
X
1
=
I(h(xi ) 6= f (xi ))
N i=1
E[err(h, f )] = Px⇠X [h(x) 6= f (x)] = Ex⇠X [Ih(x)6=f (x) ]
54