Download vectors

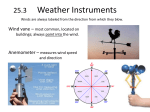
AOS 101
Atmospheric Forces
April 8/10
Vector
• Vectors have a
magnitude and a
direction (e.g. winds)
• Can be broken down
into components:

V  u ˆi  v ˆj
• |a| = magnitude of
vector a

V
u
v
• Vectors can be added:
A+B=C
Resultant
vector
B
Components can also be
added:
A
A = 3i + 1j
B = 3i + 4j
C = A + B = (3+3)i + (1+4)j
= 6i +5j
Newton’s Second Law
• Forces and accelerations are also vectors
having directions and magnitudes.
• Newton’s second law:


F  ma
• An object will accelerate in the same
direction as the force acts on it
• However, several forces will typically act
on an object simultaneously
• Hence, an object will accelerate in the
direction of the net force


Fnet  m a
where Fnet = F1 + F2 + F3 + F4 + ..., the
sum of all force vectors.
Zero Net Force
• Sometimes all forces will completely
cancel out and Fnet = 0
• In this situation, the forces are said to be
balanced
• If there is zero net force, there is zero
acceleration meaning:
– If the object is at rest, it will stay at rest
– If the object is moving, it will continue to
move at the same velocity.
Free Body Diagram
• Draw vectors representing each force
mg
mg
Fr
BOOK
mg
mg
Four Forces in the Atmosphere
•
•
•
•
Pressure Gradient Force
Coriolis Force
Friction (surface)
Centrifugal (highly curved)
1. Pressure Gradient (PG) Force
• Always points from high to low
• Always perpendicular to pressure contours
(isobars)
LOW
FPG
HIGH
P1 = 1000 hPa
P2 = 1004 hPa

1 | P2  P1 |
FPG 
a
D
• ρa = density of air ~ 1 kg/m3
• |P2 – P1| = difference in pressure (abs. value)
• D = distance between observations
• Larger pressure difference, shorter distance
(i.e. isobars closer together) results in larger
force
2. Coriolis (cor) Force
• Apparent force due to earth’s rotation
• Always perpendicular and to the right (in the
N.H.) of the wind

V
Fcor


Fcor  f | V |
• |V| = magnitude of wind (in m/s)
• f = 1.4 x 10-4 * sin(latitude)
– Midlatitudes: f ~ 1.0 x 10-4
• An increase in wind speed results in a stronger
force
• In the absence of friction, will oppose PG force
Geostrophic Balence
• PG and Coriolis forces balance:


FPG  Fcor
• How does this happen?
– Wind will increase until magnitude of Coriolis
force (fv) is the same as PG force.
• Thus, balanced wind speed can be found by:


| V |  FPG / f
LOW
HIGH
FPG
Fcor

V
P1 = 1000 hPa
P2 = 1004 hPa
• When geostrophically balenced, winds will be
parallel to isobars, with low pressure to the left
3. Frictional (Fr) Force
• Due to roughness of the earth’s surface
– Only important within 1-2 km of the ground
(planetary boundary layer)
– Negligible in free atmosphere (above 2 km)
• Always in the opposite direction of the wind

V
FFr
LOW
FPG

V
P1 = 1000 hPa
FFr
HIGH
Fcor
P2 = 1004 hPa
• At the ground, winds will not be parallel to
isobars
• Winds will cross isobars towards lower pressure
4. Centrifugal (cen) Force
• Outward “force” due to inertia while curving
• Always perpendicular to wind vector, outward
from circle

V
L
Fcen

 2
Fcen  | V | / R
• |V| = magnitude of wind (in m/s)
• R = radius of circulation
• Only important for strong winds (e.g. the
jet stream) that are highly curved.
Two possibilities
Fcen
FPG

V
Fcor
H



FPG  Fcen  Fcor
Fcen

V
Fcor
FPG
L



FPG  Fcor  Fcen
Summary
• Pressure Gradient
– ALWAYS perpendicular to isobars
– ALWAYS points from high to low pressure
• Coriolis
– ALWAYS perpendicular to wind vector
– ALWAYS (in the NH) to the right of wind vector
• Friction
– ALWAYS in opposite direction of wind vector
– Only important with 1-2 km of the ground
• Centrifugal
– ALWAYS points outward from circle, perpendicular to wind vector
– Only important for strong winds and highly curved flows
Application to Weather Maps
• Weather maps will typically be on an isobaric
surface (constant pressure sfc.)
• Height of the surface plotted instead of
pressure
• “height” features are same as “pressure”
features
– High height area is same as high pressure area
– Low height area is same as low pressure area
• PGF acts from high heights to low heights