* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson 4.1 - Advanced Geometry: 2(A)
Euler angles wikipedia , lookup
Rational trigonometry wikipedia , lookup
Poincaré conjecture wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Euclidean geometry wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
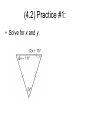
Lesson 4.1 & 4.2 ADV: 1. Triangle Sum Theorem 2. Properties of Isosceles Triangles 4.1 Warm Up: • Have a pen and a pencil out for this opening activity. • On your own, write everything you know about triangles in pencil. • You will have 3 minutes to write this information in your notes. • Then you will have discussion time with the person next to you to add anything new in pen. • Make a decision about who in your group will investigate an acute triangle and who will investigate an obtuse triangle. Investigation #1: • Split a piece of paper with your desk-mate. • One of you will draw (using a straightedge) an acute angle on your half and the other person will draw an obtuse angle on his/her half. • Cut out your triangle. • Tear off the three angles and arrange them on a line. (Draw a line if this helps.) • What do you notice about the angle measures? Triangle Sum Conjecture: • The sum of the measures of the angles in a triangle is __________. Proof of the Triangle Sum Conjecture: • Why do angles 2, 4, and 5 add up to 180º? Use deductive reasoning to explain. 4.1 Example #1: Classifying Triangles by Sides: • Name the triangle that fits the given description: Isosceles Triangles: (4.2) Investigations 1 & 2: • In your notes, do the Investigations on p. 207 – 208. • After each investigation, summarize each conjecture in your notes. Isosceles Triangles: A • Conjectures: Isosceles Triangle Conjecture: If a triangle is Isosceles, then _____________________________. If AB AC , then C Converse of the Isosceles Triangle Conjecture: If a triangle has two congruent angles, then __________________________. If B C , then B (4.2) Practice #1: • Solve for x and y. (4.2) Example #2: • Solve for the variables. (4.2) Example #3: Homework: • P. 203-205: 5, 6, 9, 10, 16 • P. 208-209: 8, 9, 18, 19, 25 Closing Activity: • Write any new conjectures in your LT. Add any helpful example of each conjecture. Be sure to define any new words.