Download Connected and occupied sites

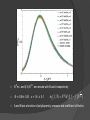
Application of Statistics and Percolation Theory
Temmy Brotherson
Michael Lam
Granular Materials

What are granular materials?
○ Macroscopic particles
○ Interaction between particles- repulsive
contact forces

Why are they studied?
○ Use
○ Properties and behavior
Indeterminants

The stacking of cannon balls

Hyper-static Equilibrium ( 6 Contact Points )

Stable Equilibrium ( Any 3 Contact Points )

Contacts become random
Hysteresis

For a particle at rest on multiple surfaces,
direction of frictional force can’t be determined

Without prior knowledge of system forces can
be determined
Statistics

Indeterminacies make straight forward
analytical approaches difficult

Numerous grains in material furthers this
difficulty

Statistical methods are a natural way to
analyze this type of system
Probability Distribution

Distributions can be used to study general
properties of forces in the system

Systems undergoing different processes can
be identified

Most likely shear Ft is about its mean value. All other forces most
probable value is near its mean.

Both compression forces share similar probability at high forces
but shear Ft are more likely to be bigger then Fn
Radial Distributions

Can be used to study the direction of
propagating forces

Net forces on system and propagation of
forces can be extrapolated.

12 contact points represents the 6 equilibrium points of the
two configurations

Represents two different configurations
Correlation

Finds the linear dependence of forces
between two grains as a function of separation

If defined as
Cor  r   F  x  F  x  r 
where F(x) is the sum of contact forces on a
grain at x

Can be use to find force chain lengths

Shear system has longer probable chains lengths in y
direction then x

Compression has equally probability in both directions
Clusters
Connected and
occupied sites
Percolation Theory

What is Percolation theory?
○
○
○
○

Numbers and properties of the clusters
f= force
fc= critical threshold force
Elaborate later on scaling exponents and
function
Use of the Percolation theory model
P( s, f )  s  [ s ( f  f c )  ]
○ s= random grain size; fc= critical threshold; 
and  are scaling exponents; =scaling
function
Mean Cluster Size


S is the mean cluster size
ns(p) is the number of clusters per lattice site
S   s 2 ns
s
S  c 3  z 2 exp( z )dz
1
c  ( f  fc )

S  c 3U ( z )
z  cs
A general form of the moment
mn ( f , N )  N n M n ([ f  f c ]N
1
2
)
 1
n  1 
 
n 

 1
 N=system size i.e. number of contacts in the packing
Why Percolation Theory?

Probability of connectivity
○ f=0, f=1
○ f< fc, f> fc
○ Force network inhomogeneity in granular materials
○ Quantification of force chains
 Threshold, fc, small and large f
 Force network variation- statistical approach

Around fc, the system shows scale invariance
○ Power-law behavior of our scaling exponents and
scaling function
○ Suggests systems with this behavior have same
properties



N-Φm2 and (f-fc)N1/2v are rescale with B and A respectively
Φ = 0.89 ± 0.01 , v = 1.6 ± 0.1
1
2
mn ( f , N )  N n M n ([ f  f c ]N )
A and B are a function of polydispersity, pressure and coefficient of friction

Plot show similar features

Problem in calculating fc

For proper scaling in x-axis proper centering is needed