* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Sensor Based Forgery detection Forensic Imaging seminar
Survey
Document related concepts
Transcript
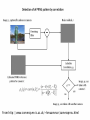
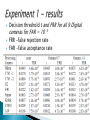
Prof. Hagit Hel-Or By Noa Privman Horesh Motivation. Image acquisition process. Sensor pattern noise. Photo-response non–uniformity noise (PRNU). Digital camera identification. PRNU-based Image Forgery Detection Digital fingerprint – We would like to have reliable, inexpensive and fast identification of digital image origin. Is the image was taken by this camera? Is a set of images were taken by the same camera? Camera Shutter Before the light reaches the sensor, it passes through the camera lenses, a blurring filter, and then through a color filter array (CFA). A de-mosaicking process is subsequently carried out. A sequence of image processing operations such as color correction, white balancing, Gamma correction, enhancing, JPEG compression, etc. also take place before the photo is saved Lens Aberrations Vignetting Spherical aberration Chromatic Aberration Lens Glare Radial Distortion Color Filter Array (CFA) CFA - a mosaic of color filters that block out a certain portion of the spectrum, allowing each pixel to detect only one specific color. The Foveon™ X3 sensor is the only sensor that does not use CFA and is able to capture all three basic colors at every pixel. Fuji Corporation The heart of every digital camera is the imaging sensor. The sensor is divided into very small minimal addressable picture elements (pixels) that collect photons and convert them into voltages that are subsequently sampled to a digital signal in an A/D converter. CCD ◦ Charge Coupled Device CMOS ◦ Complementary Metal Oxide Semiconductor Photosensitive element Charge acquired depends on the number of photons which reach the element CMOS devices are arrays of this basic element Boyle and Smith, 1969, Bell Labs (Nobel prize 2009) Converts light into electrical signal (pixels) Even if the imaging sensor takes a picture of an absolutely evenly lit scene, the resulting digital image will still exhibit small changes in intensity between individual pixels. This is due to: ◦ Shot noise (also known as photonic noise), which is a random component ◦ Sensor Pattern noise (SPN) – a deterministic component that stays approximately the same if multiple pictures of the exact same scene are taken. Photon Shot Noise Light is quantum in nature Noise due to statistics of the detected photons themselves More noise in bright parts of the image You can identify the white and black regions from the noise image Can be used for camera identification since it is present in every image. Two main components: The fixed pattern noise (FPN) - caused by dark currents. It primarily refers to pixel-topixel differences when the sensor array is not exposed to light. FPN also depends on exposure and temperature. The photo-response non-uniformity noise (PRNU) which is the dominant part of the pattern noise. Electron emission when no light Dark current noise is high for long exposures To remove (some) of it ◦ Calibrate the camera (make response linear) ◦ Capture the image of the scene as usual ◦ Cover the lens with the lens cap and take another picture ◦ Subtract the second image from the first image Original image + Dark Current Noise Image with lens cap on Result of subtraction Copyright Timo Autiokar Caused primarily by pixel non-uniformity (PNU), which is defined as different sensitivity of pixels to light caused by the inhomogenity of silicon wafers and imperfections during the sensor manufacturing process. Light refraction on dust particles and optical surfaces and zoom settings also contribute to the PRNU noise. These components are known as “doughnut” patterns and vignetting and are of low spatial frequency in nature. The output of the sensor y = (yij) can be expressed in the following form (before any other camera processing) yij = fij (xij + ηij)+ cij + εij. Where: ◦ x = (xij) – the photon counts that would be ideally registered by the sensor due to incoming light ◦ η = (ηij) - the shot noise ◦ ε = (εij) - additive random noise ◦ c = (cij) - dark current Final pixel values pij (assume to be in the range 0 ≤ pij ≤ 255), are pij = P(yij, N(yij), i, j) Where P is a non-linear function of yij, the pixel location (i, j), and values y from a local neighborhood N(yij). To verify that a specific image p was taken with camera C: ◦ Determine the camera reference pattern PC, which is an approximation to the PNU noise. ◦ The presence of the reference pattern in p will be established using correlation. Obtain an approximation to the PNU noise by averaging multiple images p(k), k = 1, …, Np. This process can be sped up by suppressing the scene content from the image prior to averaging. This can be achieved using a denoising filter F and averaging the noise residuals n(k): n(k) = p(k) – F(p(k)) From: Khanna, Nitin. Forensic camera classification: Verification of sensor pattern noise approach. Diss. Purdue University, 1740. Another benefit of working with the noise residuals is that the low-frequency components of PRNU are automatically suppressed. The larger the number of images Np, the more we suppress random noise components and the impact of the scene. using Np > 50, is recommend. Although various denoising filters can be used as F, the wavelet-based denoising filter has been reported as effective in producing good results. The denoising filter is built in two stages. ◦ In the first stage, the local image variance is estimated. Calculate the fourth-level wavelet In each subband, estimate the local variance of the original noise-free image for each wavelet coefficient. ◦ In the second stage the local Wiener filter is used to obtain an estimate of the denoised image in the wavelet domain To decide whether a specific image p was taken by camera C, the correlation ρC between the noise residual n = p – F(p) and the camera reference pattern PC, was calculated. From http://www.commsp.ee.ic.ac.uk/~hmuammar/cameraprnu.html Image database containing approximately 320 images from each camera (listed in the table) with a variety of outdoor and indoor scenes, including closeups and landscapes taken under varying light conditions Images were taken with and without the flash and with varying zoom settings. images were taken under vastly different ambient temperatures Reference pattern for each camera was calculated by averaging the noise residual (n(k) = p(k) – F(p(k))) for Np = 300 images from the database. Then, the correlation of each reference pattern with the noise residual from every image from the database was calculated. For every image from the database of 9×300=2700 images, the correlation with the reference pattern of the camera that took the image was always the highest. Decision threshold t and FRR for all 9 Digital cameras for FAR = 10−3 FRR -false rejection rate FAR -false acceptance rate Use PRNU as a unique sensor fingerprint Given two images I1 and I2, decide if they were taken with the same camera (that is unavailable) Where g is the color channel gain, γ is the gamma correction factor, K is a zero-mean multiplicative factor responsible for PRNU. is the sensor output in the absence of noise and Θ is a complex of independent random noise components. Sharp peak in NCC is indicative of the fact that both images were taken with the same camera Images coming from 8 cameras from different manufacturers with a variety of sensors and resolutions. Total of 10 images of various indoor and outdoor scenes in the raw format were taken with each camera. For each camera, device linking algorithm for matching and non-matching image pairs was run. All matching pairs (10×9/2=45) and 200 randomly chosen un-matching pairs where tested. PSR ◦ The ratio between the primary peak to the secondary peak. ◦ Used as a measure of peak sharpness. ◦ Defined as the largest value in the NCC excluding a central region around the primary peak. PSR used to evaluate the performance of the proposed method. An image pair is declared to come from the same camera if PSR ≥ Th False alarm rate of PFA = 1 – c(Th) where c is the cumulative density function of the PSR for n samples taken from a Gaussian distribution The decision threshold was set so that the probability of false alarms was PFA ≅ 5×10–5 Many works try to improve the accuracy of device linking using Sensor Pattern noise (SPN). One example is ‘Source camera linking using enhanced sensor pattern noise extracted from images’ by Li, Chang-Tsun which is presented in the following slides. It is based on the model that extract the SPN, n, from an image I using n = I – F(I), where F is a denoising function which filters out the sensor pattern noise The key limitation is that the SPN, n, can be severely contaminated by the details from the scene because details account for the highfrequency components of I as well and will remain in n Hypothesis - The stronger a signal component in n is, the less trustworthy the component should be and thus should be attenuated. Enhanced fingerprint ne , where α is a threshold decided by the user. To demonstrate the performance of the proposed sensor pattern noise enhancer with α = 7, source device linking tests was carried out on 600 photos of 1536×2048 pixels taken in JPEG format by six cameras, each responsible for 100. For each photo I, the similarity was calculate between it and six other photos, one randomly picked from each of the six cameras. The similarity between any two SPNs i and j is calculated using Let m be the photo corresponding to the maximum of the six similarity values: Photo i and j can be linked to the same source camera Cm, m ϵ [1,6]. Assumption - either the camera that took the image is available or other images taken by that camera are available The forged region is determined as the one that lacks the pattern noise. Reminder : ◦ Denoting the random shot noise as η= (ηij), the additive random noise as ϵ= (ϵij), and the dark current as c = (cij), the digitized output of the sensor y = (y ) can be expressed in the following form: yij = fij(xij + ηij) + cij + ϵij ◦ Final pixel values pij (assume to be in the range 0 ≤ pij ≤ 255), are pij = P(yij, N(yij), i, j) ij ◦ Where P is a non-linear function of yij, the pixel location (i, j), and values y from a local neighborhood N(yij). To decide whether a selected region R in image p is compatible with the pattern noise from camera C, we first calculate the correlation between the noise residual n = p – F(p) with the camera reference pattern PC The correlations is calculated for regions of the same size and shape coming from other cameras or from the same camera but at a different location within the image. Cumulative distribution function (CDF) describes the probability that a real-valued random variable X with a given probability distribution will be found to have a value less than or equal to x. generalized Gaussian distribution (or generalized normal distribution) is a parametric family of symmetric distributions. It includes all normal distribution Once having the correlation value, need to decide whether the region was tampered. Model the distribution with the generalized Gaussian distribution with cumulative distribution function G(x). Using this model, the probability that a generalized Gaussian random variable with the estimated distribution will attain the value ρ(n(R), PC(R)) or larger is R was tampered if p > 10–3 and not tampered otherwise. Assuming that the ROI have been determined manually by an operator as an area whose integrity is in question, or have been identified by one of the forgery-detection techniques and there is a need to strengthen the evidence. Selecting the ROI R Calculate ◦ The correlation ρ(n(R), PC(R)) ◦ The correlations ρ(n(Qk), PC(R)), k = 1, …, NR, for regions Qk of the same size as R coming from 90 non-tampered images obtained using 9 different digital cameras (10 from each digital camera). ◦ Using this statistical model, the p-value was calculated. Recall that if p > 10–3 the ROI was tampered and not tampered otherwise. Let y be a digital image observed at the camera output. y can be written as y = (1+k)x + θ (1) Where x is the ideal noise-free image, k the camera PRNU, and θ an additive noise term which accounts for all types of disturbances. Rewriting y as y = xk + x + θ the PRNU, k, is the only signal of interest, and the goal is to decide whether or not it comes from the camera under test A. B. C. D. Estimation of the camera PRNU (off-line). Computation of image noise residual and of derived statistics. Sliding-window pixel-wise forgery detection test. Morphological processing of test result map. The detection problem is formulated as a binary hypothesis test: the camera PRNU is absent - the pixel has been tampered the camera PRNU is is present -the pixel is genuine Where z = yk ; n is the denoising error and other disturbances in a single noise The detection test is based on the normalized correlation index between rWi and zWi , the restrictions of r and z, to a window Wi centered on the target pixel. Pixel labeling is obtained by comparing the decision statistic with a thresholdγ1. the threshold is selected to obtain the desired false acceptance rate (FAR) Morphological filtering operates on the map output by the previous test All regions smaller than 64×64 pixels, one fourth of the window size, are attributed to random errors and removed. Finally, the surviving regions are dilated with a structured element of radius 20 pixel to restore, approximately, the shape of the forged region, since many border points go lost because their correlation index is computed on mixed (forged/genuine) blocks 1. 2. 3. 4. 5. J. Lukas, J. Fridrich, and M. Goljan, ‘Digital camera identification from sensor noise’, IEEE Transactions on Information Forensics and Security, vol. 1, no. 2, pp. 205–214, 2006. C.T. Li, ‘Source camera linking using enhanced sensor pattern noise extracted from images’, International Conference on Imaging for Crime Detection and Prevention, 2009. M. Goljan, M. Chen, and J. Fridrich, ‘Identifying common source digital camera from image pairs’, IEEE International Conference on Image Processing, 2007. Lukáš, Jan, Jessica Fridrich, and Miroslav Goljan. "Detecting digital image forgeries using sensor pattern noise." Electronic Imaging 2006. International Society for Optics and Photonics, 2006. Chierchia, Giovanni, et al. "A Bayesian-MRF approach for PRNU-based image forgery detection." Information Forensics and Security, IEEE Transactions on9.4 (2014): 554-567.