Download Chapter 10

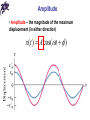
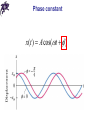
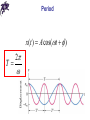
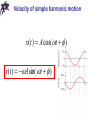
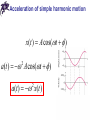
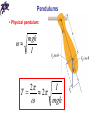
Chapter 10
Simple Harmonic Motion and Elasticity
Periodic motion
• Periodic (harmonic) motion – self-repeating motion
• Oscillation – periodic motion in certain direction
• Period (T) – a time duration of one oscillation
• Frequency (f) – the number of oscillations per unit
time, SI unit of frequency 1/s = Hz (Hertz)
1
f 
T
Heinrich Hertz
(1857-1894)
Motion of the spring-mass system
• Hooke’s law:
F  kx
• The force always acts toward the equilibrium
position: restoring force
• The mass is initially pulled to a distance A and
released from rest
• As the object moves toward the equilibrium
position, F and a decrease, but v increases
Motion of the spring-mass system
• At x = 0, F and a are zero, but v is a maximum
• The object’s momentum causes it to overshoot the
equilibrium position
• The force and acceleration start to increase in the
opposite direction and velocity decreases
• The motion momentarily comes to a stop at x = - A
Motion of the spring-mass system
• It then accelerates back toward the equilibrium
position
• The motion continues indefinitely
• The motion of a spring mass system is an example
of simple harmonic motion
Simple harmonic motion
• Simple harmonic motion – motion that repeats itself
and the displacement is a sinusoidal function of time
x(t )  A cos(t   )
Amplitude
• Amplitude – the magnitude of the maximum
displacement (in either direction)
x(t )  A cos(t   )
Phase
x(t )  A cos(t   )
Phase constant
x(t )  A cos(t   )
Angular frequency
x(t )  A cos(t   )
 0
A cos t  A cos  (t  T )
cos   cos(  2 )
cos(t  2 )  cos  (t  T )
2  T
2

T
  2f
Period
x(t )  A cos(t   )
T
2

Velocity of simple harmonic motion
x(t )  A cos(t   )
v(t )  A sin( t   )
Acceleration of simple harmonic motion
x(t )  A cos(t   )
a(t )   A cos(t   )
2
a(t )   x(t )
2
The force law for simple harmonic
motion
• From the Newton’s Second Law:
2
F  ma  m x
• For simple harmonic motion, the force is
proportional to the displacement
• Hooke’s law:
F  kx
k  m
2
k

m
m
T  2
k
Energy in simple harmonic motion
• Potential energy of a spring:
U (t )  kx / 2  (kA / 2) cos (t   )
2
2
2
• Kinetic energy of a mass:
K (t )  mv / 2  (m A / 2) sin (t   )
2
2
 (kA / 2) sin (t   )
2
2
2
2
m  k
2
Energy in simple harmonic motion
U (t )  K (t ) 
 (kA / 2) cos (t   )  (kA / 2) sin (t   )
2
2

2
2
 (kA / 2) cos (t   )  sin (t   )
2
 (kA / 2)
2
2
2

E  U  K  (kA / 2)
2
Chapter 10
Problem 40
A 1.1-kg object is suspended from a vertical spring whose spring constant is
120 N/m. (a) Find the amount by which the spring is stretched from its
unstrained length. (b) The object is pulled straight down by an additional
distance of 0.20 m and released from rest. Find the speed with which the object
passes through its original position on the way up.
Pendulums
• Simple pendulum:
• Restoring torque:
   L( Fg sin  )
• From the Newton’s Second Law:
I     L( Fg sin  )
• For small angles
sin   
mgL
 

I
Pendulums
• Simple pendulum:
at

L
s

L
mgL
 

I
mgL
a
s
I
• On the other hand
a(t )   x(t )
2
mgL

I
Pendulums
• Simple pendulum:
mgL

I
mgL


2
mL
2
I  mL
2
g
L
L
T
 2

g
Pendulums
• Physical pendulum:
mgh

I
2
I
T
 2

mgh
Chapter 10
Problem 45
The length of a simple pendulum is 0.79 m and the mass of the bob is 0.24 kg.
The pendulum is pulled away from its equilibrium position by an angle of 8.508
and released from rest. Assume that friction can be neglected and that the
resulting oscillatory motion is simple harmonic motion. (a) What is the angular
frequency of the motion? (b) Using the position of the bob at its lowest point as
the reference level, determine the total mechanical energy of the pendulum as
it swings back and forth. (c) What is the bob’s speed as it passes through the
lowest point of the swing?
Simple harmonic motion and uniform
circular motion
• Simple harmonic motion is the projection of uniform
circular motion on the diameter of the circle in which
the circular motion occurs
Simple harmonic motion and uniform
circular motion
• Simple harmonic motion is the projection of uniform
circular motion on the diameter of the circle in which
the circular motion occurs
x(t )  A cos(t   )
vx (t )  A sin( t   )
Simple harmonic motion and uniform
circular motion
• Simple harmonic motion is the projection of uniform
circular motion on the diameter of the circle in which
the circular motion occurs
x(t )  A cos(t   )
vx (t )  A sin( t   )
Simple harmonic motion and uniform
circular motion
• Simple harmonic motion is the projection of uniform
circular motion on the diameter of the circle in which
the circular motion occurs
x(t )  A cos(t   )
a x (t )   A cos(t   )
2
Damped simple harmonic motion
Fb  bv
Damping
force
Damping
constant
Forced oscillations and resonance
• Swinging without outside help – free oscillations
• Swinging with outside help – forced oscillations
• If ωd is a frequency of a driving force, then forced
oscillations can be described by:
x(t )  A(d / , b) cos(d t   )
• Resonance:
d  
Indeterminate structures
• Indeterminate systems cannot be solved by a simple
application of the equilibrium conditions
• In reality, physical objects are
not absolutely rigid bodies
• Concept of elasticity is employed
Solids
• Crystalline solid: atoms have an ordered structure
(e.g., diamond, salt)
• Amorphous solid: atoms are arranged almost
randomly (e.g., glass)
Solids
• Have definite volume and shape
• Molecules:
1) are held in specific locations by electrical forces
2) vibrate about equilibrium positions
3) can be modeled as springs connecting molecules
Elasticity
• All real “rigid” bodies can change their dimensions
as a result of pulling, pushing, twisting, or
compression
• This is due to the behavior of a microscopic
structure of the materials they are made of
• Atomic lattices can be approximated as
sphere/spring repetitive arrangements
Stress and strain
• All deformations result from a stress – deforming
force per unit area
• Deformations are described by a strain – unit
deformation
• Coefficient of proportionality between stress and
strain is called a modulus of elasticity
stress = modulus * strain
Tension and compression
• Strain is a dimensionless ratio – fractional change in
length of the specimen ΔL/Li
• The modulus for tensile and compressive strength
is called the Young’s modulus
F
L
Y
A
Li
Thomas Young
(1773 – 1829)
Tension and compression
• Strain is a dimensionless ratio – fractional change in
length of the specimen ΔL/Li
• The modulus for tensile and compressive strength
is called the Young’s modulus
Shearing
• For the stress, force vector lies in the plane of the
area
• Strain is a dimensionless ratio Δx/h
• The modulus for this case is called the shear
modulus
F
x
S
A
h
Hydraulic stress
• The stress is fluid pressure P
= F/A
• Strain is a dimensionless ratio ΔV/V
• The modulus is called the bulk modulus
F
V
B
A
Vi
Chapter 10
Problem 66
A square plate is 1.0  102 m thick, measures 3.0  102 m on a side, and has a
mass of 7.2  102 kg. The shear modulus of the material is 2.0  1010 N/m2. One
of the square faces rests on a flat horizontal surface, and the coefficient of
static friction between the plate and the surface is 0.91. A force is applied to the
top of the plate. Determine (a) the maximum possible amount of shear stress,
(b) the maximum possible amount of shear strain, and (c) the maximum
possible amount of shear deformation X that can be created by the applied
force just before the plate begins to move.
Questions?