Download A Prelude to Obstruction Theory - WVU Math Department

An Introduction to the Theory of Obstructions:
Notes from the Obstruction Theory Seminar at
West Virginia University
Adam C. Fletcher
c Spring 2009
Contents
1 The
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
Preliminaries: Definitions, Terminology,
Cells: Building Blocks of Homotopy Theory .
Building with Cells: Intuition on Complexes .
Formal Construction of CW-Complexes . . .
Deconstruction of CW-Complexes . . . . . . .
Basic Properties of CW-Complexes . . . . . .
Deconstructing Further: (Sub)Polyhedra . . .
Deformations and Homotopy . . . . . . . . .
The Homotopy Extension Property . . . . . .
Cellular Maps: A New Type of Morphism . .
and
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
Examples
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
.
.
.
.
.
.
.
.
.
1
1
2
6
7
8
10
12
14
14
2 Theories of Homology and Cohomology
2.1 Terminology of Homology and Cohomology
2.2 General Homology Theory: Points . . . . .
2.3 General Cohomology Theory: Points . . . .
2.4 General Homology Theory: Homotopy . . .
2.5 General Cohomology Theory: Homotopy . .
2.6 General Homology Theory: Spheres . . . .
2.7 General Cohomology Theory: Spheres . . .
2.8 General (Co)Homology Theories: Wedges .
2.9 Popular Homology Theories . . . . . . . . .
2.10 Popular Cohomology Theories . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
18
18
21
22
23
24
24
25
26
26
28
3 Extensibility and Obstruction
3.1 Prelude to Obstruction: The Players .
3.2 Prelude to Obstruction: Extensibility .
3.3 Algebraic Tools for Obstructions . . .
3.4 Terminology of Homotopy Groups . .
3.5 Connectivity and Hurewicz’ Theorem .
3.6 The Definition of Obstruction . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
30
30
31
32
33
35
35
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Abstract
The generalization of everyday concepts, and applying rigor thereunto, has long
intrigued the mathematician. The topic of an obstruction theory arises from
the question of deforming continuous maps, and what, exactly, holes are. Intuitively, the fundamental difference between an orange and a doughnut is that a
doughnut has a hole, and an orange does not. When shrinking a rubber band
around an orange, the rubber band will vanish; whereas the rubber band that
passes through the hole of the doughnut, or the one that encircles the doughnut
at its widest point, cannot vanish without cutting the doughnut or snapping
the rubber band. When we apply the mathematical rigor that transforms oranges, doughnuts, and rubber bands into spheres, tori, and copies of S 1 , we raise
the question of what the “empty space” in the torus actually represents. The
shrinking of the rubber band represents continuous deformations of circles and
spheres. What, then, will obstruct our continuous deformation? The answer to
this question forms the foundation of an obstruction theory.
Chapter 1
The Preliminaries:
Definitions, Terminology,
and Examples
1.1
Cells: Building Blocks of Homotopy Theory
The theory of obstructions should comfortably couched in the arms of homotopy
theory, since we wish to discuss topological spaces, the maps of continuous
functions, and how these maps are attached to the spaces. In order to study the
loops, discs, and spheres that we wish to, we must define some basic homotopic
ideas. The first such idea is that of cells.
Definition 1.1.1. An open n-cell is a subspace, en , of a topological space X
such that en is homeomorphic to an open n-sphere, the patch of Euclidean space
of all points less than one unit from the origin.
It bears mentioning, here, that cells are not the only building blocks of topological spaces. Depending on the branch and purposeful application of the mathematics involved, one could consider blades, which represent n-dimensional triangles (points, arcs, triangles, tetrahedra, etc.), instead. Mathematical physicists
often make use of cubes, which are defined by inductively connecting 2n of the
n-dimensional cubes at right angles to each other (points, arcs, squares, cubes,
hypercubes, etc.). In a topological since, however, these bases are equivalent. It
is only when considering the intrinsic geometry at n ≥ 2 that we see a difference
between the cell, the blade, and the cube; the n-sphere, the n-triangle, and the
n-square.
1
CELLS
BLADES
CUBES
points in space: 0!cells
open arcs in space: 1!cell
boundary is the 0!sphere
open discs in space: 2!cells
boundary is the 1!sphere
open spheres in space: 3!cells
boundary is the 2!sphere
Figure 1.1: Low Dimensional Building Blocks
1.2
Building with Cells: Intuition on Complexes
Now that we have the building blocks of a homotopy theory, we must mix
our mortar and build our homotopic foundation. Let us begin by doing so
“intuitively,” and then applying some rigor.
Definition 1.2.1. Let X 0 be called the 0-skeleton of a topological space, X,
and consist of a collection of 0-cells of X.
Definition 1.2.2. The n-skeleton, X n , of a space X is built inductively by
attaching a number of n-cells, enα , (where α is an element of an indexing set)
to X n−1 by objects called attaching maps, denoted ϕnα : S n−1 → X n−1 , which
identify the boundaries of each n-cell to the previous skeleton in some prescribed
manner.
One can then create a finite complex, X n , or an infinite complex
[
X=
X n.
n∈N
Although spaces of this latter type form an infinite class, this “mega-union”
seems to be the only such class of infinite complexes. Since this is the case,
and the class of finite complexes is fair richer, it is with the finite case that we
concern ourselves.
Example. Consider, as an example, the construction of the two-sphere, S 2 , as
the union of a 0-cell and a 2-cell. The attaching map, ϕ2 , attaches the boundary
of e2 (which is S 1 ) to the single 0-cell, as shown in Figure 1.2.
2
2!cell
A circle is the boundary
of a disc
0!cell
Figure 1.2: Example: Cell Structure of the Sphere, S 2
Figure 1.3: Example: Cell Structure of the Torus, T 2
3
Example. Consider the slightly more complicated construction of the twotorus, T 2 . To our end, we consider the so-called “flat-torus,” which is represented as the unit square, I 2 , under identifications. We think of the “interior”
of the square as a 2-cell (a disc). We then form the torus by identifying the
“top” to the “bottom” of the square, and the “left” side to the “right” side
of the square. That is, ϕ11 , shown in red in Figure 1.3, maps one identified
1-sphere to the meridian, and ϕ12 , shown in blue in the same figure, maps the
other identified 1-sphere to the equator. Finally, the identification of the edges
induces the identification of all four “corners” of the square as a single point.
Thus, ϕ0 maps the identified 0-sphere to the point of intersection on the torus
of the 1-spheres.
Now, for each n-cell, the attaching maps connect the boundary of the cell to a
lower skeleton. The n-cell itself, however, must also be “attached” to the space
in question. This map is called the characteristic map, is denoted
Φnα : enα → X
(where the overline denotes topological closure), and extends the attaching map,
ϕnα , by mapping the disc homeomorphically onto the interior of enα .
Example. Returning to Figure 1.2 above, we see that the characteristic map
of the sphere is given by
Φ 2 : e2 → S 2
that contracts the boundary of e2 to e0 via a straight-line homotopy.
Example. The torus in Figure 1.3 grants
Φ 2 : e2 → T 2
defined by the identification of edges and, subsequently,
Φ11 and Φ12 : e1i → S 1
for i = 1, 2, by identifying endpoints of each edge.
Both of the these examples, however, have something in common. Both are orientable, in that the sphere and the torus both have an outward-pointing tangent
vector field. In topology, we need to consider as many different types of spaces
as possible, and so, we turn to the non-orientable surfaces. One such example
is the projective plane.
The two-dimensional real projective plane has been equivalently described as
the result of identifying all four edges of a square to a single edge, with opposite
pairs attached with opposite orientations; as a bi-gon (a circle with two pinched
points) with opposite edges identified with opposite orientations; as identifying
all lines through the origin in R2 to a single line; or identifying antipodal points
of S 1 to each other. We can take these ideas, most preferably the last, and
4
SPHERES
PROJECTIVE
PLANES
0
0
S and RP
1
1
S and RP
2
2
S and RP
Figure 1.4: Constructing Real Projective Space
generalize to all n ∈ N, resulting in an n-dimensional real projective space, the
first three of which are shown in Figure 1.4.
For our purposes, however, we wish to see these real projective spaces as having
a complex structure. Accordingly, we build the projective spaces inductively.
First, RP0 is merely the identified point, e0 . As a union of the identified edge and
its base point, RP1 is e1 ∪e0 . Similarly, RP2 consists of the identified hemisphere
and its equator, which is a copy of RP1 . Thus, RP2 = e2 ∪ e1 ∪ e0 . This pattern,
then, generalizes to all n, where RPn is the identified hemi-(n − 1)-sphere and
its equator, resulting in
n
[
RPn =
ei .
i=0
Example. As for the characteristic maps for the projective plane, we have
Φ2 : e2 → RP2 and Φ1 : e1 → RP1
given by identifying antipodal points of the respectively dimensioned spheres.
5
1.3
Formal Construction of CW-Complexes
Let us now apply mathematical rigor to our idea of a CW-complex.
Definition 1.3.1. Recall that a space holds the T2 separation axiom, or
is Hausdorff, if, for any two elements of the space, there are mutually disjoint
neighborhoods of these points. That is to say, for each x, y ∈ X, there exists a
neighborhood U of x and a neighborhood V of y so that U ∩ V = ∅.
Example. The usual topology in Rn is Hausdorff, as is the subspace topology
on any X ⊆ Rn . One must be careful, however, not to assume that all spaces
are Hausdorff. The finite complement topology (where a set U is open if and
only if X − U is a finite set) is very rarely Hausdorff.
We will require a CW-complex to be Hausdorff, since we wish to regard the
space as an embedding in Rn . This is the case, since we are building the space
from cells, which are (fairly trivial) embeddings into Rn .
As stated previously, we wish to ignore the case of the infinite cell skeleton. To
this end, we will make our second requirement for a space to be a CW-complex
that the characteristic maps attaching each closed cell, eα n , to X must map the
cell boundaries to a finite number of spheres. This is to say that the image of
each attaching map is a finite union of spheres. J.H.C. Whitehead called this
property closure-finiteness, as it implies an enclosure of each skeleton within a
compact space (compact, both in the literal and the mathematical sense).
Example. It is not difficult to see that the examples shown in Figure 1.2 and
Figure 1.3 are closure-finite.
Example. The following example, due to [10] fails in this closure-finiteness
criterion. Consider the space X produced by bounding a two-cell by three onecells, then by adjoining a zero-cell at intervals of 1/n along one of the one-cells,
as shown here:
Figure 1.5: Munkres’ Non-CW-Complex
Notice that the attaching map of the 2-cell consists of infinitely many 0-spheres,
and so the space fails to be closure-finite. The “boundary” of the 2-cell (that
is, the space formed by the union of the 1-cells and 0-cells), however, is closurefinite, since the attaching map of each 1-cell consists of at most two 0-cells.
6
Our final criterion for status as a CW-complex will involve a topology placed
on the space.
Definition 1.3.2. Let X be a topological space, and let A ⊆ X. We say that
A is closed in X if A ∩ eα n is closed in the cellular subspace topology for each
n. This induced topology is known as the weak topology on X.
In conclusion, we say that a space X is a CW-complex, or has a CW-complex
structure on it, if the following three criteria hold:
• X is Hausdorff;
• X is closure-finite; and
• X is embued with the weak topology on its cells.
As a matter of interest, it is the weak topology on the space, along with the
closure-finiteness of the complex that gives the CW-complex its name.
Example. Returning to Munkres’ triangle (Figure 1.5), we notice that the
closure-finiteness is the only criterion which the space fails. The space, as a
subset of Euclidean two-space in the usual topology, is Hausdorff; and usuallyclosed sets are weak-closed sets, as the weak topology is finer than the usual
topology. That is, for each closed subset A, for each α and each n, the A ∩ eα n
are closed.
Example. The “boundary” of Munkres’ triangle (that is, the union of the
one- and zero-cells), however, is, indeed, a CW-complex, since the Hausdorff
and weak topology criteria are inherited from the greater triangle, and we have
discussed the closure-finiteness of this space.
1.4
Deconstruction of CW-Complexes
As is the case in many branches of mathematics, our primary aim when introducing a topic is to define an object in a category, to show that it is well
defined (which will be shown shortly), to give some examples and properties of
the object (which also will be given shortly), and, thence, to break the object
into smaller pieces. Although out of order, we shall do this last, first.
Definition 1.4.1. A subcomplex of a CW complex, X, is a closed subspace,
A ⊆ X, that is a union of cells of X. The pair (X, A) is called a CW pair.
Example. Since the RPn are constructed of unions of skeletons, the RPk are
subcomplexes for all k < n.
Example. If S n is merely en ∪ e0 , as is the usual construction, none of the ei
for 0 < i < n is a subcomplex of S n . This seems to make S n “simple,” in a
manner of speaking. We can, however, think of S n as enN ∪ enS ∪ S n−1 , where
eN and eS represent the northern and southern hemi-n-spheres, respectively.
The (n − 1)-sphere should be defined in terms of its hemispheres and lower
dimensional spheres, as well.
7
Figure 1.6: CW-Decomposition of a Sphere
1.5
Basic Properties of CW-Complexes
In preparation for defining obstructions, we wish to build some necessary groundwork on the properties, both topological and homotopic, of CW-complexes.
Some will seem to be extremely important, and others, merely as passing interests. We, however, have a purpose for each, which will become apparent in
time.
Proposition 1.5.1. A compact subspace of a CW-complex, X, is contained in
a finite subcomplex of X.
Proof. We follow the method of [4]. Let X be a CW-complex, and let C be a
compact subspace thereof.
We claim, first, that C intersects only finitely many cells. For a contradiction
of this claim, we assume C intersects infinitely many cells, and let xi be the
points in C ∩ ei for each i ∈ N. Further, we define the set S of these intersection
points. That is,
S = {x1 , x2 , . . . }.
As a disjoint union of points, we have that S is closed in X. Notice, trivially,
that S ∩ {e0α } = S is closed in X 0 . Assume, then, that S ∩ X n−1 is closed in
X n−1 , and we consider the closed n-cells, eα n . Since S is closed, and attaching
n
maps are continuous, ϕ−1
α (S) is closed in eα . Since the characteristic map is an
−1
extension of the attaching map, Φα (S) = eβ m ∪ ϕ−1
α (S), for some m, making
this inverse image closed in eα n , as well. We have, then, that in the n-skeleton,
S ∩ X n is closed. Inductively, then, this is the case for all n. Since X is a CWcomplex (and, hence, a union of these skeletons), S is closed in X.
By the same argument, any subset of S is closed, and, hence, S carries the discrete topology. Since S is a compact space (any closed subspace of a compact
space is), S must be finite. As this contradicts our assumption, we conclude
that S cannot be infinite, so C intersects but finitely many cells.
8
Notice that the cell eα n is contained in a finite subcomplex of X, since, for each
n, ϕα (eα n ) is a finite union of (n − 1)-and-smaller spheres, which is compact.
Thus, by our proposition, eα n is contained in a finite subcomplex of X. Since
C is contained in a finite number of cells, it is contained in a finite number of
finite subcomplexes of X, which, in turn, is a finite subcomplex of X.
Proposition 1.5.2. The finite product of CW-complexes is a CW-complex.
Proof. We, again, follow the method of [4]. For our purpose, it will suffice to
show that the product of two CW-complexes is a CW-complex, and, thence,
we can proceed inductively to the arbitrarily finite case. Let X and Y be CWcomplexes with characteristic maps ΦX and ΦY , respectively.
We claim that (ΦX × ΦY ) : enα × em
α → X × Y is the characteristic map for the
product space. To this end, we must show that X × Y has a complex structure
on it. Recall that the product of Hausdorff spaces is Hausdorff.
Moreover, if the image of attaching maps in X consists of n spheres and the
image of the attaching maps in Y consists of m spheres, then the image of the
attaching maps in the product space consists of at most mn spheres, and, so, is
finite.
Finally, we consider the weak topology on the product space. If A ⊆ X ×Y, then
A ⊆ πX (A) × πY (A), where πi are the projections into each factor space. If we
put a “compactified” topology on X × Y (think the weak topology), having A
compact grants that the projections are also closed and compact. Since πX (A)
and πY (A) are compact, they are contained in a finite subcomplex of their
respective factor space, namely
n
[
ei and
i=1
m
[
ej .
j=1
We notice, however, that
n
[
i=1
ei ×
m
[
ej ⊆
j=1
n,m
[
(ei × ej ).
i,j=1
Hence, A is contained in the union of crossed cells, and the intersection of A
with a closed cell will result in a closed set in the subspace topology. Thus, a
closed subspace of the product space is closed in the weak topology, giving the
product space a CW-structure.
9
1.6
Deconstructing Further: (Sub)Polyhedra
Although not all topological spaces are CW-complexes, an arbitrary space X
could, feasibly, be homeomorphic to a CW-complex, and could have a CWstructure placed upon it. Such spaces are referred to as polyhedra. The
“well-behaved” polyhedra, those that consist of finitely many cells, are called
finite polyhedra. Moreover, a closed subset Y of a polyhedron X that consists
of a union of cells is called a subpolyhedron, where the complex structure is
referred to as the subcomplex. This is consistent with other branches of mathematics, where a portion of a full object also has the properties of the mother
object (cf. subsets, subgroups, submanifolds, etc.).
In order to consider continuous deformations of a polyhedron, we will need to
consider a homotopy, which can be represented as a continuous function through
a “time variable.” To this end, we consider the space crossed with the time variable, or X × I, where I is the unit interval. We will call this space the cylinder
space of the polyhedron, X, denote it by Cyl(X), and note that Cyl(X) is, itself, a polyhedron. This is a result of the fact that, if X has a complex structure
in terms of the enα , then the sets enα × 0, enα × 1, and enα × (0, 1) form a complex
structure on the cylinder X × I, due to Proposition 1.5.2. The union of these
crossed cells, then, gives that X × I is generated by the cells of X crossed with
the cells of I, which are 0, 1, and (0, 1).
Figure 1.7: Simplified Cylinder Space
10
Now that we have a complex structure on the cylinder space of a polyhedron,
we should study the properties of continuous functions working on this new
polyhedron. Doing so will allow us to use the tools of homotopy theory on all
polyhedra. We begin with the following named theorem.
Proposition 1.6.1 (Borsuk’s Lemma). Let Y be a subpolyhedron of a polyhedron X. Then there is a continuous map Γ : X × I → (X × 0) ∪ (Y × I) that
serves as the identity on the range.
Figure 1.8: Cylinder Space for Borsuk’s Lemma
Borsuk’s Lemma could effectively be called the “Tank Draining Lemma.” The
essential (and intuitive) idea behind this lemma is that whatever the fish do in
the full fish tank will eventually be mirrored on the floor of the empty tank,
after it is drained, with the possible exception of the “inner storage chamber.”
As time, t, decreases from one to zero, X − Y is continuously deformed to the
initial state (X × 0), whereas Y remains unchanged.
Proof. Let X be a polyhedron, and Y be a subpolyhedron of X. A standard
proof technique in the realm of polyhedra is induction on both number and
dimensionality of cells. We proceed in this wise, following [1].
We first consider the case when Y = X − en for some n. If n = 0, then the map
(
(x, 0) if x ∈
/Y
Γ(x, t) =
(x, t) else
11
is the desired map. Let n > 0, then, and consider the attaching map
ϕn : ∂en = S n−1 → X n−1
of the n-cell, and the corresponding characteristic map Φn : en → X of the disc.
We will denote by ι : I → I the identity map on the unit interval, [0, 1]; and
(Φn × ι) : en × I → X × I
given by
(Φn × ι)(∗, t) = (Φn (∗), t)
is a characteristic map on the cylinder space of the polyhedron.
Now, we define ψ : en × I → (en × 0) ∪ (S n−1 × I) by the mapping
(∗, t) 7→ (∗, tχ(∗)),
where χ is a (analytic) characteristic map, taking on the values of 0 and 1 pertaining to whether or not ∗ ∈ ∂(en ). We notice that ψ serves as the identity on
the range.
Let (x, t) ∈ X × I. Since X is a polyhedron, ((Φn )−1 (x), t) ∈ en × I. Then
ψ(((Φn )−1 (x), t)) ∈ (en × 0) ∪ (S n−1 × I)
and
(Φn × ι)(ψ(((Φn )−1 (x), t))) ∈ (X × 0) ∪ (Y × I).
We must recall that multiplication and analytic-characteristic functions are continuous. Notice that this function serves as the identity on its range and is
continuous, since the inverse of a local homeomorphism, product of continuous
functions, and compositions of continuous functions are all continuous. We define Γ to be this function.
In the general case, we build a “larger” Γ by iterating the previous Γ over all
0-cells, then 1-cells, 2-cells, and so on, in X − Y .
1.7
Deformations and Homotopy
In the effort to apply rigor and dimensionality to the idea of shrinking rubber
bands on our spaces, we need to define the continuous deformation of spheres.
Definition 1.7.1. Let X be a topological space and Y be a subspace of X.
There is a continuous deformation of X onto Y if there is a collection of
continuous maps ft : X → X for t ∈ I so that f0 = X, f1 = Y, and ft is the
identity when restricted to Y, for all t ∈ I.
12
Definition 1.7.2. Let X and Y be a topological spaces. There is a homotopy
of X to Y if there is a collection of continuous maps ft : X → Y for t ∈ I and a
continuous map H : X × I → Y so that H(x, t) = ft (x), f0 = X, and f1 = Y .
Notice that a continuous deformation is just a homotopy of a space to one of its
subspaces.
The collection of equivalence classes of these deformations/homotopies on the
space X form an algebraic group, called the fundamental group, of the space,
which is denoted π1 (X).
It is worthwhile for the reader to examine, both intuitively and algebraically,
the deformations represented below.
Figure 1.9: Discs are “Nullhomotopic”
Notice that the unit disc can be continuously deformed to its origin by the
“straight line homotopy,” given by h(x, t) = x(1 − t). Any topological space
that can be continuously deformed to a point is said to be nullhomotopic.
Figure 1.10: The Punctured Plane is Homotopic to the Circle
Furthermore, notice that the so-called punctured plane, the space R2 − {0},
can be continuously deformed to the unit circle, again, by the “straight line
homotopy,” this time give by
x
h(x, t) = x(1 − t) +
t,
||x||
where || · || is the Euclidean norm on R2 .
13
The Möbius band, a non-orientable surface, can be continuously deformed to its
core circle, as well. Again, this is done by a straight-line homotopy that maps
each point of the Möbius band orthogonally onto the core circle.
The punctured torus can be continuously deformed to a wedge of two 1-spheres.
This can be visualized using the flat torus, as in Figure 1.3. The punctured flat
torus can be seen to be very similar, then, to the punctured plane, in Figure
1.10. This retracts the “interior” of the flat torus to its boundary edges, each of
which represent a circle. These circles are joined at the identified point, creating
the topological space S 1 ∨ S 1 .
1.8
The Homotopy Extension Property
Borsuk’s Lemma gives us a way to extend (or contract) a given continuous map
from a “larger” space to a “smaller” space in a continuous manner. It is, however, a fairly specific lemma and is reliant on the cylinder space of the contrived
specific space. We wish to generalize this extendibility to a broader category
of spaces without relying as much on cylinder spaces. The homotopy extension
property is, therefore, the foundational property for the study of extensions.
Proposition 1.8.1 (Homotopy Extension Property). Let X be a complex, and
let Y be a subcomplex, thereof. Furthermore, let Z be a general topological
space. Given f0 : X → Z and a continuous deformation gt : Y → Z for t ∈ I,
with f0 = g0 on Y, then there is a continuous deformation ft : X → Z of f0 so
that ft = gt for all t ∈ I on Y.
Proof. Let X, Y , Z, f0 , and gt be as defined in the conditional. Denote by
ĝ : Y × I → Z the continuous deformation defined by
ĝ(y, t) = gt (y).
By Borsuk’s Lemma, there is a continuous Γ = fˆ : X × I → (X × 0) ∪ (Y × I)
that is the identity on the range. That is, fˆ(x, t) = ĝ(x, t) whenever x ∈ Y
or when t = 0. If x ∈ Y, then, fˆ and ĝ agree; making fˆ an extension of ĝ.
The restriction that fˆ(x, 0) = ĝ(x, 0) gives that f0 = g0 . Thus, the extension
preserves the deformations by g and the function f0 = g0 , as desired.
1.9
Cellular Maps: A New Type of Morphism
As a brief interlude into category theory, we consider our position. We have a
collection of objects (our CW-complexes), and we have broken them down (into
subcomplexes). It seems that we wish to study continuous mappings on these
objects. Better yet, we need to studying continuous mappings between these
objects. When working with numerical, set theoretic, or algebraic mathematics, we often choose operations (plus, minus, times, divide; intersection, union,
cartesian product; tensor products); when working with geometry or topology,
14
we choose operators (divergence, gradient, curl; differential forms). In the category of cell complexes, our morphism will need to be a continuous mapping
between two objects.
Definition 1.9.1. Let X and Y be two cell complexes. A cellular map is a
continuous function f : X → Y so that the image of each skeleton in the domain
is contained within the corresponding dimensional skeleton of the range. That
is to say, f (X n ) ⊆ Y n for all n.
Cellular maps serve two larger purposes: first, after statement of the next proposition, we can approximate any topological space by a CW-complex, and, so,
we can simplify the way we see some complicated spaces. Additionally, we will
study relationships between several different types of continuous maps, most
likely on CW-complexes (when discussing higher-dimensional homotopy groups
and [co]homology classes). We will consider these as cellular maps.
Proposition 1.9.2 (Cellular Approximation Theorem). Let X and Y be cell
complexes. A continuous map f : X → Y is homotopic to a cellular map.
Moreover, if f is cellular on a subcomplex X 0 of X, the homotopy is constant
on X 0 .
One should note here that in other texts, many authors revert to the cellular
approximation theorem after developing homology theory, and so use relative
homology to prove a generalized (relative) case of the Cellular Approximation
Theorem first, with this version as a corollary. We follow [1], however, and prove
the theorem directly.
Proof. As has been seen before, we will proceed by induction on cells, both by
order and by number.
We notice that if X and Y have only zero-skeletons; that is to say, that X and
Y are discrete point-sets, then the proof is trivial. Since the image of any map
between the two will fall within the zero-skeleton of Y, it is a cellular map.
Consider the inductive case, where X is the result of an n-cell being joined to a
subcomplex, X 0 , and Y is the result when an m-cell (where m > n) is joined to a
subcomplex, Y 0 . Using the characteristic maps, we chart a system of coordinates
onto en and em and define a function f0 : X → Y . For those readers familiar
with the study of manifolds, this will be similar (but not congruent!) to sending
charts from Rn into the manifold [9, 2].
15
n
X
e
e
m
Y
Figure 1.11: Construction of f0 for Cellular Approximation
The Map: Define f0 to be the composition of the following maps:
• (Φn )−1 : X → en , the characteristic map for the selected n-cell;
• ι : en → em , the inclusion map; and
• Φm : em → Y , the characteristic map for the selected m-cell; with
• f0 (X 0 ) ⊆ Y 0 (for the induction process).
By construction, then, f0 is a composition of continuous functions and is, therefore, continuous. We may, then, approximate f0 by differentiable functions (and,
in particular, polynomials) via the Weierstrass Approximation Theorem.
The Approximation and Deformation: We denote by f∗ : X → Y this
Weierstrass approximation of f0 . Since the inclusion ι : en → em is proper, due
to strict inequality of dimension, there is a y0 ∈ Y that is not in the image,
f∗ (X). Let x0 ∈ (Φm )−1 (y0 ) ⊆ em , and let ht be a deformation of em − {x0 }
onto itself that is constant on the boundary of the closed cell; that is, S m−1 .
The Homotopy: For t ∈ [0, 1], let
(
(Φm ◦ ht ◦ (Φm )−1 ◦ f∗ )(x) for f∗ (x) ∈ Φm (em )
0
ft =
.
f∗ (x)
otherwise
Notice that f00 = f∗ (since h0 is an identity) and that ft0 gives a continuous
deformation of f∗ to f10 , both of which map X → Y . Notice, moreover, that
f10 (X) ⊆ Y 0 , and, by construction, is constant on X 0 . Our proposition, then, is
proven in the special case; and induction on cells concludes the proof.
16
As another note of interest, a map f is said to be regular at a point x if its
coordinate maps (built from the characteristic maps as above) have continuous
first-order partial derivatives. This is equivalent to the nonsingularity of the
Jacobian matrix. If the Jacobian determinant is positive or negative, so, too,
is the point denoted. It can be shown (in a manner similar to the proof of the
Cellular Approximation Theorem), that cellular maps can be approximated by
regular maps.
17
Chapter 2
Theories of Homology and
Cohomology
2.1
Terminology of Homology and Cohomology
Definition 2.1.1. A topological space X on which a CW-complex structure can
be placed is called a polyhedron. A subspace of X on which a CW-complex
structure can also be placed is called a subpolyhedron.
Definition 2.1.2. Let G be a set of objects, and let g, h, k ∈ G. Let · be the
product operation on G. The set G is said to be closed under · if g ·h ∈ G for all
g, h. The set G is said to be associative under · if g·(h·k) = (g·h)·k for all g, h, k.
An identity of the set is an element e ∈ G so that e · g = g · e = g for all g. An
inverse of an element g is an element g −1 ∈ G so that g · g −1 = g −1 · g = e. The
set G is said to be an algebraic group if the set is closed and associative under
its operation, contains an identity, and contains inverses for all its elements.
Definition 2.1.3. Let G and H be algebraic groups. A map f : G → H is said
to be a homomorphism of groups if f (xy) = f (x)f (y) for any x, y ∈ G. This
is to say, a homomorphism preserves products from group to group.
As a matter of notation, unless otherwise defined, we shall, throughout this
chapter, let X and Y be polyhedra, and let Z be a subpolyhedron of X. We
will denote by Hn (X) an algebraic group, called the n-th homology group, and
by H n (X) another algebraic group, called the n-th cohomology group. The
reader should be forwarned that [5] refers to this group as the contrahomology group, instead. We, further, consider general homomorphisms f : X → Y ;
and their induced homology (respectively, cohomology) homomorphisms
f∗ : Hn (X) → Hn (Y ) and f ∗ : H n (Y ) → H n (X). Between these groups, we
also have the boundary and coboundary maps ∂ : Hn (X/Z) → Hn−1 (Z) and
δ : H n (Z) → H n+1 (X/Z).
18
Now, in order for us to consider homology and cohomology groups, we should
have a given theory within which we may work. The framework for the general
homology or cohomology theory is given by a list of axioms, or postulates, that
will allow us to base our proofs on “facts.” One must be careful in interpretation, however. The following definitions include the axiom system of a general
homology (or cohomology) theory. In order to show that a certain homology
theory is valid, one must show that the listed axioms do, indeed, hold.
This being said, let us define our theories.
Definition 2.1.4. Using the notation above, a collection of polyhedra, groups,
homomorphisms, and boundary maps form a homology theory if and only if
the following criteria are met:
• Composition of induced homomorphisms is well-behaved: (g ◦f )∗ = g∗ ◦f∗
• Identities are preserved by induction: id∗ : Hn (X) → Hn (X) is the identity automorphism
• Diagrams commute; that is, ∂ ◦ f∗ = g∗ ◦ ∂, for the homomorphisms below
X with subspace Z
f
Y with subspace T
g
H n(X/Z)
f
*
H n(Y/T)
boundary
H n!1(Z)
boundary
g
!*
H n!1(T)
Figure 2.1: Diagrams Commute in Homology Theories
• Homotopy is perserved by induction: f ∼ g ⇒ f∗ = g∗
• Homology pair sequences are exact
• Hn (S 0 ) = 0 for all n 6= 0. The “nontrivial” homology group, called the
coefficient group, will be denoted G.
19
Definition 2.1.5. In a similar manner, we define a cohomology theory by
the following criteria:
• Composition of induced homomorphisms is “devaheb-llew”:
(g ◦ f )∗ = f ∗ ◦ g ∗ ; that is to say, well-behaved in the contravariant sense
• Identities are preserved by induction: id∗ : H n (X) → H n (X) is the identity automorphism
• Diagrams commute; that is, f ∗ ◦ δ = δ ◦ g ∗ , for the homomorphisms below
X with subspace Z
f
Y with subspace T
g
H n(X/Z)
f*
H n(Y/T)
boundary
n!1
H (Z)
boundary
g*
H n!1(T)
Figure 2.2: Diagrams Commute in Cohomology Theories
• Homotopy is perserved by induction: f ∼ g ⇒ f ∗ = g ∗
• Cohomology pair sequences are exact
• H n (S 0 ) = 0 for all n 6= 0. The “nontrivial” cohomology group, called the
coefficient group, will be denoted G.
In the following sections, we will prove certain computational results that hold
for all homology (respectively, cohomology) theories. We should recall that not
all collections of spaces, morphisms, and boundary operators will form a homology or cohomology theory. The following, however, will hold whatever the fixed
theory is.
20
2.2
General Homology Theory: Points
In a general homology theory, the following results regarding topological points
and sets of points are true.
Proposition 2.2.1. Let X = {x} be a one-point space. Then, for each n, we
have Hn (X) = 0.
Proof. Consider {x} ⊆ {x}, the map i : {x} → {x}, and the quotient map
j : {x} → {x}/{x} = {x}. Then the exact homology sequence yields
j∗
i
∂
∂
∗
Hn ({x}) → Hn ({x}/{x}) = Hn ({x}) → · · ·
· · · → Hn ({x}) →
Since i∗ and j∗ are identity automorphisms, they are isomorphisms. In particular, j∗ is injective, and its kernel is 0. Since the sequence is exact; that is
to say, since im(i∗ ) = ker(j∗ ), we have that the image of i∗ is also 0. As an
isomorphism, though, i∗ is surjective; that is, Hn ({x}) = 0.
Proposition 2.2.2. Let X = {x1 , x2 , . . . , xk } be a k-point space, with coefficient group G. Then
k−1
Y
H0 (X) =
G
i=1
and Hn (X) = 0 for n > 0.
Proof. We proceed inductively. We notice that the statement is true when k = 1,
by Proposition 2.2.1. Consider the case, then, when k > 1. Let
X = {x1 , . . . , xk } and Y = {x1 , . . . , xk−1 }.
Then X/Y = {x1 , xk }. Let i be the inclusion map, Y → X and j be the quotient
map, X → X/Y. Then, for all n 6= 0, the exact sequence gives
j∗
i
∂
∂
∗
· · · → Hn (Y ) →
Hn (X) → Hn (X/Y ) → · · ·
to be, inductively,
∂
j∗
i
∂
∗
··· → 0 →
Hn (X) → 0 → · · · ,
which makes Hn (X) = 0, as well.
On the other hand, if n = 0, we see
j∗
i
∂
∂
∗
· · · → H0 (Y ) →
H0 (X) → H0 (X/Y ) → 0
to be, through induction,
∂
0→
k−2
Y
j∗
i
∂
∗
G→
H0 (X) → G → 0.
i=1
21
As a split exact sequence, this gives H0 (X) to be the product of the other two
groups; that is,
k−1
Y
H0 (X) =
G,
i=1
as desired.
2.3
General Cohomology Theory: Points
In a general cohomology theory, the following results regarding topological
points and sets of points are true.
Proposition 2.3.1. Let X = {x} be a one-point space. Then, for each n, we
have H n ({x}) = 0.
Proof. Consider {x} ⊆ {x}, the inclusion map i : {x} → {x}, and the quotient
map j : {x} → {x}/{x} = {x}. Then the exact cohomology sequence yields
j∗
i∗
δ
δ
· · · ← H n ({x}) ← H n ({x}) ← H n ({x}/{x}) = H n ({x}) ← · · ·
Since i∗ and j ∗ are identity automorphisms, they are isomorphisms. In particular, i∗ is injective, and its kernel is 0. Since the sequence is exact; that is to say,
since im(j ∗ ) = ker(i∗ ), the image of j ∗ is also 0. As an isomorphism, though, j ∗
is surjective; that is, H n ({x}) = 0.
Proposition 2.3.2. Let X = {x1 , x2 , . . . , xk } be a k-point set, with coefficient
group G. Then
k−1
Y
G
H 0 (X) =
i=1
n
and H (X) = 0 for n > 0.
Proof. We proceed inductively. We notice that the statement is true when k = 1,
by the result in Proposition 2.3.1. Consider the case, then, when k > 1. Let
X = {x1 , . . . , xk } and Y = {x1 , . . . , xk−1 }.
Then X/Y = {x1 , xk }. Let i : Y → X be the inclusion map, and j : X → X/Y
be the quotient map. Then, for all n 6= 0, the exact sequence gives
j∗
δ
i∗
δ
· · · → H n (X/Y ) → H n (X) → H n (Y ) → · · ·
to be, inductively,
δ
j∗
i∗
δ
· · · → 0 → H n (X) → 0 → · · · ,
which, as a series of isomorphisms, makes H n (X) = 0, as well.
22
On the other hand, if n = 0, we see
j∗
δ
i∗
δ
· · · → H 0 (X/Y ) → H 0 (X) → H 0 (Y ) → 0
to be, through induction,
δ
j∗
i∗
0 → G → H 0 (X) →
k−2
Y
δ
G → 0.
i=1
As a split exact sequence, though, this gives H 0 (X) to be the product of the
two factor groups; that is,
k−1
Y
H 0 (X) =
G,
i=1
as desired.
2.4
General Homology Theory: Homotopy
Our study of polyhedra will give us a larger scale on which to study homology
theory. We wish, however, to calculate as few homology groups as possible. It
is to this end that we appeal to homotopic spaces. Since topology is a study
of spaces that can be bent and stretched continuously, we hope that homotopic
spaces will have the same homologous qualities.
Proposition 2.4.1. Homotopic polyhedra have isomorphic homology groups.
Proof. Let X and Y be homotopy equivalent polyhedra. Then, by the definition
of homotopy equivalence, there exists a homotopy f : X → Y and a homotopy
g : Y → X so that g ◦ f : X → X and f ◦ g : Y → Y are the identities on their
respective polyhedra.
By the second and first axioms (respectively) of homology theory, we see that
idHn (X) = (idX )∗ = (g ◦ f )∗ = g∗ ◦ f∗
and that
idHn (Y ) = (idY )∗ = (f ◦ g)∗ = f∗ ◦ g∗ .
Hence, there are inverse automorphisms passing between Hn (X) and Hn (Y ),
making these groups isomorphic.
Example. Closed balls, en , of any dimension, n, have trivial homology groups.
Proof. Since there is a deformation retract of en to a point (the straight line
homotopy), the closed ball and a point have the same homology groups. Since,
in Section 2.2, we found that the homology groups of a point are always trivial;
hence, so, too, are those of a closed ball.
23
2.5
General Cohomology Theory: Homotopy
In a similar manner to the previous section, we wish to show that cohomology
is also preserved by homotopies. The proof is identical, mutatis mutandi.
Proposition 2.5.1. Homotopic polyhedra have isomorphic cohomology groups.
Proof. Let X and Y be homotopy equivalent polyhedra. Then, by the definition
of homotopy equivalence, there exists a homotopy f : X → Y and a homotopy
g : Y → X so that g ◦ f : X → X and f ◦ g : Y → Y are the identities on their
respective polyhedra.
By the second and first axioms (respectively) of cohomology theory, we see that
idH n (X) = (idX )∗ = (g ◦ f )∗ = f ∗ ◦ g ∗
and that
idH n (Y ) = (idY )∗ = (f ◦ g)∗ = g ∗ ◦ f ∗ .
Hence, there are inverse automorphisms passing between H n (X) and H n (Y ),
making these groups isomorphic.
Example. Closed balls, en , of any dimension, n, have trivial cohomology groups.
Proof. Since there is a deformation retract of en to a point (the straight line
homotopy), the closed ball and a point have the same cohomology groups. Since,
in Section 2.3, we found that the cohomology groups of a point are always
trivial; hence, so, too, are those of a closed ball.
2.6
General Homology Theory: Spheres
As mentioned above, if we are to study the homology of polyhedra, we must
study the homology of our cells. Since the Cellular Approximation Theorem
allows us to approximate almost any “nice” topological space by CW-complexes,
almost any “nice” topological space has homology generated by its cell structure.
We have now been given the homology of 0− and 1−cells and their topological
closures. In order to determine the homology of other complexes, we must study
the boundaries of these closed cells, the spheres.
Proposition 2.6.1. Spheres, S n , of any dimension, n, have trivial homology
groups for all k 6= n, and have homology group G for k = n, where G = H0 (S 0 ).
Proof. Notice that, by our homology axioms, the statement is trivial (assininely
so) for n = 0.
For our sequence, consider X = en and its “boundary,” Y = S n−1 . Then the
quotient space, X/Y = S n , by the standard construction of spheres. Again, we
consider i : Y → X as the inclusion map, and j : X → X/Y as the quotient
24
map. This gives our homology exact sequence (often called the Mayer-Vietoris
sequence), then, to be
j∗
i
∂
j∗
i
∂
∂
∗
∗
Hk−1 (X) → Hk−1 (X/Y ) → · · · ,
Hk (X) → Hk (X/Y ) → Hk−1 (Y ) →
· · · → Hk (Y ) →
which becomes, by substitution,
j∗
i
∂
j∗
i
∂
∂
∗
∗
· · · → Hk (S n−1 ) →
Hk (en ) → Hk (S n ) → Hk−1 (S n−1 ) →
Hk−1 (en ) → Hk−1 (S n ) → · · · .
By the homology of points (and all things homotopic thereunto), we have that
i
∂
j∗
i
∂
j∗
∂
∗
∗
0 → Hk−1 (S n ) → · · · .
0 → Hk (S n ) → Hk−1 (S n−1 ) →
· · · → Hk (S n−1 ) →
∼ Hk−1 (S n−1 )
is exact. The exactness of the sequence grants that Hk (S n ) =
for each n, k. Moreover, repeated iterations of this isomorphism grant that
Hk (S n ) = Hk−n (S 0 ). We recall, however, that Hm (S 0 ) is trivial for all m 6= 0
(which is when k 6= n), and is G when m = 0 (or k = n), as desired.
2.7
General Cohomology Theory: Spheres
For the same reason as above regarding the homological nature of spheres, we
desire to extract the cohomological nature of spheres. The result, not surprisingly, is the same.
Proposition 2.7.1. Spheres, S n , of any dimension, n, have trivial cohomology
groups for all k 6= n. Moreover, these spheres have cohomology group G for
k = n, where G = H 0 (S 0 ).
Proof. Again, by the cohomology axioms, we roll our eyes at the n = 0 case.
For our sequence, consider X = en and its “boundary,” Y = S n−1 . Then the
quotient space, X/Y = S n , by the standard construction of spheres. As per
usual, we consider the inclusion map, i, and the quotient map, j. This gives
our cohomology exact sequence (often called either the Mayer-Vietoris or,
misleadingly, the de Rham sequence), to be
j∗
δ
i∗
j∗
δ
i∗
δ
· · · → H k−1 (X/Y ) → H k−1 (X) → H k−1 (Y ) → H k (X/Y ) → H k (X) → H k (Y ) → · · · ,
which becomes
j∗
δ
i∗
j∗
δ
i∗
δ
· · · → H k−1 (S n ) → H k−1 (en ) → H k−1 (S n−1 ) → H k (S n ) → H k (en ) → H k (S n−1 ) → · · · .
By the above results, the cohomology of a closed ball is the same as that of a
point, so the sequence becomes
δ
j∗
i∗
δ
j∗
i∗
δ
· · · → H k−1 (S n ) → 0 → H k−1 (S n−1 ) → H k (S n ) → 0 → H k (S n−1 ) → · · · .
The exactness of the sequence grants that H k−1 (S n−1 ) ∼
= H k (S n ) for each n, k.
k
Repeated iterations of this isomorphism grants that H (S n ) ∼
= H k−n (S 0 ). We
m
0
recall that H (S ) is trivial for all m 6= 0 (which is when k 6= n), and is G
when m = 0 (or k = n), as desired.
25
2.8
General (Co)Homology Theories: Wedges
Since we wish to study polyhedra, in general, and not merely their cells, piecemeal, we need to somehow combine the cells and consider what happens to their
homology or cohomology as a result of said combination. The most common
combination is the topological wedge.
Definition 2.8.1. Let X and Y be topological spaces. Then the wedge sum
of the two spaces, denoted X ∨ Y is the so-called “one-point union,” the space
resulting from identifying one point, x0 , of X to one point, y0 , of Y.
One should be aware, however, that, although the wedge sum is sometimes called
the wedge product, this is not the same as the exterior product, ∧. Although this
exterior (wedge) product is important in the study of manifolds and differential
forms, it is outside the scope of this chapter.
Wp
Proposition 2.8.2. If X = i=1 S n , then
Hn (X) =
p
Y
G
i=1
and X has trivial homology groups otherwise.
Wp
Proposition 2.8.3. If X = i=1 S n , then
H n (X) =
p
Y
G
i=1
and X has trivial cohomology groups otherwise.
Proof. The proof of each of these is the same, mutatis mutandi, and is similar
to that of Proposition 2.2.1, where we merely change {xi } to Sin .
2.9
Popular Homology Theories
Now that we have the general definition of a homology theory, and have seen
some properties held by all such considerations, we define, as a matter of interest,
several of the more popular homology theories. The reader should keep in mind,
however, that these are not the only homology theories in existence; however,
these are the theories that receive the most attention from the mathematical
community at large.
Homology Theory (Simplicial Homology). A homology theory that considers triangulations of a topological space and the cycles and boundaries of said
triangulations.
26
As stated in Chapter 1, a simplex is an n-dimensional triangle. Thus, a simplicial complex consists of an n-triangulation of the space. With each k-simplex,
σi , we can define a k-chain, consisting of formal sums,
N
X
ai σi .
i=1
If the k-chains form a “loop” of sorts within the space; that is to say, if the
k-chain has no boundary, and is, therefore, in the kernel of the boundary map,
the chain is said to be a cycle. On the other hand, if the chain is the image
of some boundary map, we call it a boundary. Homology groups, then, are
defined in terms of cycles modulo boundaries.
Homology Theory (Singular Homology). A homology theory built on the
result that all manifolds of dimension three or lower have a triangulation. Continuous maps send a simplicial structure to a manifold. Such maps form chain
complexes, with cycles and boundaries relating thereunto.
Singular homology is a homology theory for those topologists who really want
to be algebraists. The theory is more categorical and algebraic. Built from simplicial homology, this theory depends on the uncountably many triangulations
that map from a simplex to a manifold. Each complex of chains is acted upon by
chain maps (induced between chain groups by homomorphisms between manifolds) and boundary operators. In a similar manner to the simplicial homology,
the kernel of the boundary operator is defined to be the collection of cycles,
and the image of the boundary operator is the collection of boundaries. Again,
homology groups are defined in terms of cycles modulo boundaries.
Homology Theory (Cellular Homology). A homology theory that considers
the attaching of cells to a topological space, the cellular map chains created
thereby, and kernels and images of the resultant boundary operators.
In a manner similar to that of singular homology, we can consider the mapping
of cells to topological surfaces via attaching and characteristic maps. As we
have seen above, cellular maps are the desired homomorphisms to accomplish
this. Since we wish to define homology classes to be invariant under homotopy,
we consider the classes of cellular maps. This, again, results in a chain complex.
Induced cellular maps create chains, where boundary operators move from one
dimension to the next lowest dimension. Again, kernels and images of these
boundary operators are used to define the homology classes of a space.
Because of the natural use of spheres and discs in our topological thinking, in
the sequel, we shall prefer to use cellular homology. Low-dimensional topologists often use simplicial or singular homologies, as they can be concerned with
certain triangulations of a space. (The Euler characteristic and Gauss-Bonnett
formulas in geometry are results of a triangulation.)
27
Although we shall not prove it here, these three homology theories are equivalent. We refer the reader to [4] for the proof, but point out that the equivalence
of simplicial and singular homology is dependent on the fact that both require
triangulation. Since homology is preserved by homotopy (as in the axioms),
and, thus, by continuous maps, the homology groups in simplicial homology
should be preserved by those of singular homology. Similarly, there is an equivalence between cellular and singular homologies at the categorical level. Both
are concerned with the chain map complexes, and these maps are often homotopic. This results in a correspondence between the chain complexes, and,
so, the homology groups that are defined by both systems as cycles modulo
boundaries.
Homology Theory (Morse Homology). A homology theory defined on a smooth
(differentiable) manifold with a Riemannian metric, dependent on the critical
points of the manifold. This flavor of homology is often used in the study of
flows over a smooth manifold, as in thermodynamics, or the like.
First of all, for more information than is given here, we refer the reader to
[7]. Now, if X happens to be a Riemannian manifold, then it has a tangent
space centered at each x ∈ X. Thus, the differential, dfx , of a smooth function
f : X → R at x is defined. We say that x is a critical point of f if dfx = 0.
Moreover, the Morse index of a point is the number of negative eigenvalues of
the Hessian matrix (the matrix with second partial derivatives of the function).
A chain complex (or module) for Morse homology is built of free Z-modules (or
free abelian groups) generated by the index n critical points of our given function. The boundary operator between consecutively indexed chains provides a
count of the gradient flow lines. For a proof that the Morse homology is, indeed,
a valid homology theory, as well as for a number of examples of its use, we refer
the reader to [7].
It is a rather amazing fact, which makes up the body of the third chapter of
[7], that Morse homology is, in fact, isomorophic to singular homology; and,
therefore, to the other two previously mentioned homologies.
Homology Theory (Floer Homology). A generalization of Morse homology
that uses tools of gauge theory and symplectic geometry. This is the “flavor
of the month” in terms of current research in homology theory, and where, in
eventuality, the author will head.
2.10
Popular Cohomology Theories
Similarly, we wish to discuss, as a matter of interest, several of the more popular
flavors of cohomology theory. To this end, there are three large categories of
cohomology theories. The first of these are the Eilenberg-Steenrod cohomology
theories. We shall explore these below. There are also the cohomology theories
that loosen one of the Eilenberg-Steenrod axioms, and depend on K-theory and
28
cobordism theory. These can be seen in the study of elliptical curves and in
algebraic geometry. Lastly, there are the “rogue” cohomologies. These last
are concerned with Lie algebraic representation theory, quantum cohomology
groups, and the Novikov cohomology.
Definition 2.10.1 (Eilenberg-Steenrod Axioms). As defined in [10], an EilenbergSteenrod cohomology satisfies the six general cohomology axioms, along with
an excision axiom; then the relative homology (with coefficients in G) between
X and a subset A, denoted H n (X, A; G) is isomorphic to that of the resultant
spaces after removal (or excision) of an open set, H n (X − U, A − U ; G).
Cohomology Theory (Simplicial, Singular and Cellular Cohomologies). These
cohomology theories are defined in terms of simplices, the triangulation maps,
and the attaching maps of cells, in a similar manner as were given in the definition of their homology theories. As duals to their respective homologies, these
three cohomologies are isomorphic, as well.
Cohomology Theory (de Rham Cohomology). A cohomology theory defined
in terms of differential forms, permutation groups thereof, and exterior (wedge)
products, with boundary operators being defined in terms of exterior derivatives.
De Rham cohomology is popular, as it is dual to the singular homology. This
provides another isomorphism of cohomologies. For more information on the de
Rham cohomology, we refer the reader to [9].
Cohomology Theory (Čech Cohomology). A more categorical cohomology
theory, defined in terms of directed sets and directed limits. We refer the interested reader to [10] for a more precise definition, proof of several of the
Eilenberg-Steenrod axioms, and examples. Most interestingly, however, is the
fact (contained in [10]) that the Čech cohomology is not isomorphic to the other
cohomology theories. Due to its definition in terms of limits, the topologist’s
sine curve has different Čech cohomology classes than, say, singular cohomology
classes.
29
Chapter 3
Extensibility and
Obstruction
3.1
Prelude to Obstruction: The Players
We now have a majority of the tools needed to discuss the idea of an obstruction to the extension of continuous mappings on a topological space. Before
proceeding, we remind the reader that we shall begin generalizing the concepts
covered, and so must give a few point-set topological definitions.
Definition 3.1.1. A space X is said to be path-connected if, for each pair
x, y ∈ X, there is a continuous function f : [0, 1] → X so that f (0) = x and
f (1) = y; that is, between each pair of points in X, there is a continuous path.
Example. Real space, in any dimension, is path-connected. The path between
any vector x and vector y is given by the line (1 − t)x + ty.
Example. The deleted comb space, a subspace of R2 consisting of the line
segment [0, 1]×{0}, the segments { n1 }×[0, 1] for each n, and the point {0}×{1},
is not path connected. This is because the point {0} × {1} is isolated from the
other points in the space. It is of interest, however, that the deleted comb space
is connected, since there is no open neighborhood of {0} × {1} that misses all
other points of the space.
In this chapter, we shall denote by each, the following:
K
Kn
L
n
K
Y
a complex
the n-skeleton of K
a subcomplex of K
the space L ∪ K n
a path-connected space
n
One should notice that K denotes the entire subspace L with any additional
n-cells. Alternatively, this is the entire n-skeleton of K unioned with any higher
order cells contained in the subspace, L.
30
3.2
Prelude to Obstruction: Extensibility
In order that we discuss obstructions to extension of continuous maps, we must
first define and generalize the extension.
Definition 3.2.1. If f : L → Y is any function, then fˆ : K → Y is said to be
an extension of f if fˆ is continuous, and fˆ = f on L. Recall that, via Borsuk’s
Lemma (Prop. 1.6.1) and the Homotopy Extension Property (Prop. 1.8.1),
such extensions are possible.
Definition 3.2.2. A function f : L → Y is said to be n-extensible over K if
n
f has an extension over K of K.
Proposition 3.2.3. Every map f : L → Y is 1-extensible over K.
1
Proof. Notice that K = L ∪ K 1 , the space L with all 1-cells (or paths) of Y.
Since Y is path-connected, extensions will consist of concatenations of paths of
Y with those in f (L). Thus, f extends, and, by definition, f is 1-extensible.
Definition 3.2.4. The supremum of the n for which f is n-extensible is called
the extension index of f over K.
Proposition 3.2.5. Homotopic maps have the same extension index.
Proof. Let f : L → Y and g : L → Y, with f ∼ g on L. Further, let fˆ be an
n
extension of f. Define ĝ to be fˆ on K − L and g on L. This is still continuous,
n
as f ∼ g on L. Then there is a homotopy ĝ ∼ fˆ, since g ∼ f on K − L; so g
extends, and the index of g is at least that of f. Similarly, we obtain the reverse
inequality, giving f and g the same extension index.
Proposition 3.2.6. Let p be a map between path-connected spaces Y → Y 0 ,
let L, L0 ⊆ K, K 0 , respectively, and let k be a cellular map K 0 → K. Then if
f : K → Y is n-extensible over K, the composition
p ◦ f ◦ k : L0 → Y 0
is also n-extensible, but over K 0 .
Proof. Since k is cellular, we have k(L0 ) ⊆ L. If f : L → Y is n-extensible over
K, then f : k(L0 ) → Y is n-extensible over K, and, therefore, the composition
f ◦ k : L0 → Y is n-extensible over K 0 . Moreover, since the image of f (L) under
p is still path-connected, we see that p ◦ f is still n-extensible over K. Then,
repeating the previous argument, we see that p ◦ f ◦ k is still n-extensible, but
over K 0 , as desired.
Proposition 3.2.7. The extension index of f is a topological invariant.
Proof. Let f : L ⊆ K → Y be n-extensible, and let g : K 0 → K be a homeomorphism, where K 0 is homologous to K. Then, by the Cellular Approximation
31
Theorem, g can be approximated by cellular maps. We denote this approximation as g 0 .The composition of these cellular maps with f are still n-extensible,
by Proposition 3.2.6, and any map homotopic to f ◦ g 0 : K 0 → Y will also be
n-extensible by Proposition 3.2.5. Thus, the extension index of a map is a
topological invariant.
3.3
Algebraic Tools for Obstructions
In order to complete our definition of an obstruction, we will still need some
algebraic tools. We wish to review some of these definitions, give a few examples,
and proceed along our way. For more information, we refer the interested reader
to [3].
Definition 3.3.1. Let A be a set and G be a group. The group action
of G on A is a mapping • : G × A → A that satisfies the properties that
g • (h • a) = (gh) • a, and that 1G • a = a, for all a ∈ A and g, h ∈ G.
Example. The trivial action of G on A is given by g •a = a for all a ∈ A, g ∈ G.
Notice that this is, indeed, an action, since 1G • a = a, and g • (h • a) = g • a = a,
whereas (gh) • a = a. This action is a “boring” one that completely ignores the
group. It treats the entire group G as the identity to each element of A.
Definition 3.3.2. We also say that G acts simply on A if the trivial action
is the action considered.
Example. The action of G on itself by left multiplication is given by the formula
g • h = gh for all g, h ∈ G. Notice that this is, indeed, an action. First of
all, 1G • h = 1G · h = h, since h ∈ G. Also, for g, h, k ∈ G, we have that
g • (h • k) = g • (hk) = g(hk) = (gh)k = (gh) • k. This action of a group on itself
is merely the multiplication within the group.
Example. A concrete example of the action by left multiplication is the multiplication of reals. Officially, this will be • : R∗ × R∗ → R∗ given by x • y = xy,
where R∗ = R − {0}.
Example. The nonzero scalars act on the field of three-space vectors by multiplication in the following way: Let • : R∗ × V → V be defined as
α • hv1 , v2 , v3 i = hαv1 , αv2 , αv3 i .
Notice that this is, in fact, a group action. The identity (1) multiplies to every
component of the vector, leaving the vector unchanged. Moreover, multiplying through twice produces the same result as multiplying the scalar product
through.
Example. A group can act on itself by conjugation if we define
• : G × G → G by g • h = ghg −1 for all the g, h ∈ G.
32
This is, in fact, a group action, since (for all g, h, k ∈ G)
1G • h = 1G · h · 1−1
G = 1G · h · 1G = h,
and since
g•(h•k) = g•(hkh−1 ) = g(hkh−1 )g −1 = (gh)k(h−1 g −1 ) = (gh)k(gh)−1 = (gh)•k.
3.4
Terminology of Homotopy Groups
In some instances, it is easier to compute homotopy groups than it is to compute
homology groups. We, therefore, provide some review of homotopic groups. For
the interested reader, the examples contained herein are exercises in [4].
Definition 3.4.1. The fundamental group, π1 (X, x0 ) is the collection of equivalence classes of maps f : e1 → X with ∂e1 = x0 .
Definition 3.4.2. Similarly, the n-th homotopy group, πn (X, x0 ) is the collection of equivalence classes of maps f : en → X with ∂en = x0 .
Definition 3.4.3. A space X is said to be n-simple if and only if, for each
x0 ∈ X, the group π1 (X, x0 ) acts simply on πn (X, x0 ).
Example. Let X ⊂ R3 be the union of n lines through the origin. Then π1 (X)
∗
2n−1
Z. Recall that R3 − {(0, 0, 0)} deformation retracts to S 2 , by the
is
i=1
normalization map (that is, vector v is mapped to v/||v||). By the same retract,
R3 − X is homotopy equivalent to S 2 − {x1 , x2 , . . . , x2n }, where the 2n points
are those at which the missing n lines pierce the sphere. Since S 2 − {1 point}
is homotopy equivalent to the plane, we have only 2n − 1 holes in the plane.
Thus,
π1 (R3 − X) ∼
= π1 (S 2 − {x1 , . . . , x2n }) ∼
= π1 (R2 − {x1 , . . . , x2n−1 }) ∼
=
∗
2n−1
i=1
Z,
as desired.
Example. Let X be the quotient space of S 2 obtained by identifying the north
and south poles to a single point. Since we only identify the poles, X “looks
like” a handled sphere:
2 !cell
S2
~
0!cell
1!cell
X therefore consists of one 2-cell, one 1-cell, and one 0-cell. There is one generator (coming from the 1-skeleton); and the relation is the trivial one; that is,
the one-cell attaches to itself by the zero-cell. Thus, π1 (X) ≈ Z/0 ≈ Z.
33
Example. Consider the quotient space of a cube I 3 obtained by identifying
each square face with the opposite square face via the right-handed screw motion
consisting of a translation by one unit in the direction perpendicular to the face
combined with a one-quarter twist of the face about its center point. Consider
the illustration of this lens space:
Notice that there is one three-cell, the “space” bounded by this object. There
are three two-cells, created by the identification of pairs of the six faces. There
are four one-cells, shown in the figure by blue, green, red, and black lines. There
are also two zero-cells. These are created by the identification of various terminal and initial points of the oriented one-cells. The points enclosed in purple
circles in the figure are identified when considering those vertices with “red-in,
green/blue/black-out,” and those enclosed in brown circles are identified when
considering those vertices with “red-out, green/blue/black-in.”
In order to compute π1 of this space, we label the red one-cells a, the green
one-cells b, the black one-cells c, and the blue one-cells d. Using multiplicative
notation, we see that
abd−1 c = acb−1 d = adc−1 b = 1.
Since all expressions contain a on the left, we multiply by a−1 to get
bd−1 c = cb−1 d = dc−1 b = a−1 .
Notice that, if a = 1, b = i, c = j, and d = k we get that the inverses are
the negative quaternions, and these quaternions satisfy the relation. Thus,
π1 (X) = Q8 , the group of quaternions.
2
2
Example. We wish to √
show
√ that π21 (R 2− Q ) is uncountable. Consider as a
base point the element ( 2, 2) ∈ R −Q . Let t be an irrational number. Then
the “square” loop going from
√ √
√
√
√
√
√ √
√ √
( 2, 2) to ( 2, t+ 2) to (t+ 2, t+ 2) to (t+ 2, 2) and back to ( 2, 2)
34
is a loop in π1 (R2 − Q2 ), since, with at least one coordinate of each ordered pair
not in the rationals, each point on the loop is in R2 − Q2 . Notice that, since
the rationals are dense in R, there is an element (p, q) ∈ Q2 enclosed in each
loop, thus, this square loop, dependent on the irrational, t, is a generator for
π1 (R2 − Q2 ). Since ¬ Q is uncountable, there are uncountably many t values
with which to construct these loops. Therefore, there are uncountably many
generators for π1 (R2 − Q2 ).
3.5
Connectivity and Hurewicz’ Theorem
In order to characterize obstructions, we must link the ideas of homotopy and
homology. We do so by defining another class of topological spaces, and by
proving an important theorem.
Definition 3.5.1. A space X is said to be n-connected if it is path-connected
and πm (X) = 0 for all m ≤ n.
Example. Points are n-connected for all n, since points are trivially pathconnected and have trivial homotopy groups.
Example. Sets consisting of k distinct points (where k ≥ 2) are not n connected
for any n, since k-point sets are not path connected.
Example. The n-sphere, S n , is n-connected, since the homotopy groups are
trivial for all dimensions except that of the sphere, itself.
Example. The standard torus is 0-connected, but not 1-connected. Recall that
π1 (T 2 ) = Z ∗ Z, where the generators of the free groups are the equatorial and
meridinal circles. All spaces are trivially 0-connected.
Proposition 3.5.2 (Hurewicz’ Theorem). If X is an (n − 1)-connected polyhedron with n > 1, and x0 ∈ X, then the so-called natural homomorphism,
hn : πn (X, x0 ) → Hn (X) is an isomorphism.
Proof. [Note: The statement of Hurewicz’ Theorem in [6] is for simplicial
complexes, rather than polyhedra, but the proof, which we follow here, is correct,
mutatis mutandi.]
3.6
The Definition of Obstruction
Let K be a polyhedron, with a subpolyhedron, L. Further, let Y be a pathn
connected n-simple space (cf. Definition 3.4.3), and choose a map g : K → Y.
Let σ be an (n + 1)-cell of K. This requires, then, the boundary of σ to be an
n-sphere, which is contained in the n-skeleton of K. In symbols,
n
∂σ = S n ⊆ K n ⊆ K .
35
We then define gσ = g|∂σ, the restriction of g to the n-sphere. Notice that gσ
is an element of πn (Y ).
Define an (n + 1)-cochain, cn+1 (g), of K by
[cn+1 (g)](σ) = [gσ ]
for each (n + 1)-cell of K. This cochain is called the obstruction of the map g.
Example. Consider the Möbius band. Let g : complex structure → möbius.
Let σ1 be the boundary circle, and let σ2 be the “interior” disc. Notice that,
while [c1 (g)](σ1 ) = [g|∂σ1 ] = [g|0] = 0, represents the lack of obstruction, and
would, therefore, allow extension over 1-cells; the second obstruction,
[c2 (g)](σ2 ) = [g|∂σ2 ] = [g|S 1 ]
is absorbed by the boundary circle of the Möbius band. This will create an
obstruction to the attachment of discs to the Möbius band, and explains why
the Möbius band is nonorientable.
Figure 3.1: The Möbius Band
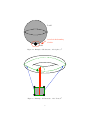
Example. Consider the usual torus in R3 . Let σ1 be either of the identified
edges (the equator or the meridian) of the torus; let σ2 be the “interior” disc
that is mapped by the characteristic map to the surface of the torus. Moreover,
consider σ3 , some solid sphere. Now, consider g : complex structure → torus.
Notice that, while
[c1 (g)](σ1 ) = [g|∂σ1 ] = [g|0] = 0
allows extension on 1-cells, and
[c2 (g)](σ2 ) = [g|∂σ2 ] = [g|aba−1 b−1 ] = [g|0] = 0
under the quotient topology (where a and b are the identified edges), grants
orientability, we see an issue with the third obstruction class. Notice that
[c3 (g)](σ3 ) = [g|∂σ3 ] = [g|S 2 ],
36
will represent the “donut hole” in the center of the torus and the inner “jelly
filling.” This will create an obstruction to the attachment of solid spheres to the
torus, which is known as handling.
Figure 3.2: Obstructions in a Torus
Thus endeth the first semester’s notes. The reader is invited to continue on the obstruction journey at
http://math.wvu.edu/~fletcher/MATH797.html.
37
Bibliography
[1] Boltyanskii, V.G. Basic Concepts of Homology and Obstruction Theory.
Russ. Math. Surv. 21 (1966), 113-132.
[2] do Carmo, Manfredo. Riemannian Geometry. Birkhäuser, Boston, 1992.
[3] Dummitt, David and Richard Foote. Abstract Algebra. John Wiley and
Sons, Hoboken, New Jersey; third edition, 2003.
[4] Hatcher, Allen. Algebraic Topology. Cambridge University Press, New York,
2001.
[5] Hilton, P.J. and S. Wylie. Homology Theory: An Introduction to Algebraic
Topology. Cambridge University Press, London, 1960.
[6] Hu, Sze-Tsen. Homotopy Theory. Academic Press, New York, 1969.
[7] Hutchings, Michael. Lecture notes on Morse homology (with an eye toward
Floer theory and pseudoholomorphic curves. Unpublished, 2002. Website:
http://math.berkeley.edu/˜hutching/teach/276/mfp.ps.
[8] Olum, Paul. Obstructions to Extensions and Homotopies. Ann. Math., II.
52 (July 1950), 1-50.
[9] Marsden, Ib and Jorgen Tornehave. From Calculus to Cohomology: De
Rham cohomology and characteristic classes. Cambridge University Press,
New York, 1997.
[10] Munkres, James. Elements of Algebraic Topology. Benjamin/Cummings
Publishing Company, Menlo Park, California, 1984.
[11] Spanier, Edwin H. Algebraic Topology. McGraw-Hill Book Company, New
York, 1966.
[12] Steenrod, Norman. The Topology of Fibre Bundles. Princeton University
Press, Princeton, New Jersey, 1951.
[13] Whitehead, George W. Homotopy Theory. MIT Press, Cambridge, Massachusetts, 1966.
38