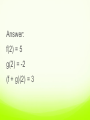Download Lesson 102: Sums of Functions, Products of Functions

Lesson 102:
Sums of Functions,
Products of Functions
Recall that functional notation has several
advantages. The first is that it allows us to identify the
equations being considered. For instance, if we have
the three equations
y=x+3
2
y=x–6
2
y = 2x + 5
We can name them as equation f, equation g, and
equation h. if we use functional notation, we would
use f(x), g(x), and h(x) instead of y.
f(x) = x + 3
2
g(x) = x – 6
2
h(x) = 2x + 5
If we add two of these equations,
we get an equation for the sum.
The sum of equations f and h is
f(x) = x + 3
h(x) = 2x + 5
2
f(x) + h(x) = 2x + x + 8
2
We see that f(x) + h(x) means that we
have added the f equation and the h
equation. Often we use the following
notation to mean the same thing.
(f + h)(x)
This means that we have added the f
equation to the h equation. The
domain for the new equation is all
numbers that were common to both
of the original domains.
Example:
Given f(x) = x + 3; D = {Reals},
2
and g(x) = x – 6; D = {Integers},
find (f + g)(2).
Answer:
f(2) = 5
g(2) = -2
(f + g)(2) = 3
Example:
Given f(x) = x + 3; D = {Reals},
2
and h(x) = 2x + 5; D = {Negative
Integers}, find (f + h)(5).
Answer:
Since 5 is not a member of the
domain of h(x) we say that the
problem has no answer or an
empty set.
When we multiply two functions, the
product is also a function. If we have the
equations
h(x) = x + 3; D = {Reals}
2
g(x) = x – 6; D = {negative
integers}
And we multiply the h equation by the g
equation, we get the product h(x)g(x).
h(x)g(x) = (x + 3)(x –2 6)
h(x)g(x) = x +
3x
–
6x
18
3
2
Instead of writing h(x)g(x) to designate the
product of the two functions, we find it
convenient to write
hg(x)
The notation hg means that the h equation
has been multiplied by the g equation in the
same way that
(h + g)(x)
Means that the h equation and the g
equation have been added.
Example:
Find hg(-4) where h(x) = x + 3; D =
2
{reals}, and g(x) = x – 6; D =
{Negative integers}
Answer:
hg(-4) = -10
Example:
Find fg(-4) where f(x) = x + 3; D =
{Reals}, and g(x) = x – 5; D =
{Positive integers}.
Answer:
-4 is not a member of the domain
of g(x); so it is not a member of the
domain fg(x). Empty set.
HW: Lesson 102 #1-30