Download HS.A-REI.B.3

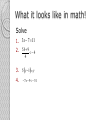
Math Moment –
Automotive Technologies
HS.A-REI.B.3 Solve linear equations and
inequalities in one variable, including
equations with coefficients represented
by letters.
Materials
Note-taker
 Worksheet

Automotive Technologies
HS.A-REI.B.3 Solve linear
equations and inequalities in one
variable, including equations with
coefficients represented by
letters
AKA Solving equations and
inequalities
Bellwork

Think about the many ways of
communicating.

Write 2 on your note-taker

Share with your partner.
Math Check

What is the difference between
and equation and an inequality?

Identify if the symbol is for an
equation or an inequality.
=
>
 
Math Check

Inverse operations – an operation
that undoes another operation.
Inverse operations
 + and –
  and 
Steps for solving equations
and inequalities
1.
◦
◦
Simplify each side of the equation or
inequality
Use the distributive property
Combine like terms
Move variables to one side and the
numbers to the other
3. Use inverse operations to undo
addition/subtraction
4. Use inverse operations to undo
multiplication/division
2.
Be careful
The steps in solving equations and
inequalities are the same UNLESS you
multiply or divide by a negative.
 If you do multiply or divide by a
negative the direction of the inequality
reverses or flips.

Why does it reverse?
We need to stay true to arithmetic
 Example

36 is a true statement
What it looks like in math!
Solve
1. 3x  711
2.
5b  9
 4
4
3. 5 y 1 y
4.
7x  9   51
You try!
1.
9 x  624
2.
40  28x 138
Auto Example

A replacement part for Cara’s
automobile costs $22.50. The
mechanic charges $25 per hour
for making the repair. How many
hours could the repair take if the
total bill is under $100.00?
x = hours
$22.5025x$100.00
You try!

The Ace Garage assesses a $15 “shop charge”
plus $20 an hour for labor. How many hours of
labor did a repair take if the total charge was
less than $85?
x = hours
$15.00  20x $85.00
Two Estimates

Professor Kleinwort receives two
estimates for the repair of his antique
sedan. The first shop will charge $595
for parts plus $22.50 per hour for
labor. A second shop offers to repair
the car for $700 plus $19 per hour for
labor. How many hours of labor must
be involved in order to make the
second estimate the cheaper?
x = hours
$595  $22.50x $700  $19x
3-MINUTE CLOSURE
OUTCOME STATEMENTS
I need more
help
with . . .
PROPERTY OF AZ CTE CURRICULUM CONSORTIUM, 2013