* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Solve the equation by graphing the related function.
Survey
Document related concepts
Transcript
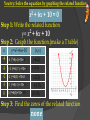
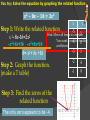
Warm Up 1) Use the graph to Identify the following: a)Vertex: (-2,-1) b) Zeros: -3 and -1 c) Range: R: y≥-1 d)Domain: D: all real numbers e) Line of symmetry: x=-2 f)Minimum/Maximum: Minimum=-1 Solving quadratics by graphing Objective California Standards 21.0 Students graph quadratic functions and know that their roots are the x-intercepts. Also covered: 23.0 Steps for solving Quadratic Equations by Graphing Step 1: Write the related function. Step 2: Graph the function. Step 3: Find the zeros of the related function Two Zeros One Zero No zeros Two Roots One Root No real Roots Finding Roots of Quadratic Polynomials Find the roots of x2 + 4x + 3 Step 1: Write the related equation. x2 + 4x + 3=0 y= x2 Step 2: Graph the function. (make a T table) Step 3: Find the zeros of the related function The roots are at -1 and -3. + 4x + 3 x -4 y 3 -3 0 -2 -1 -1 0 0 3 What is/are the root(s)? You try: Solve the equation by graphing the related function. x2 + 6x + 10 = 0 Step 1: Write the related function. y= x2 + 6x + 10 Step 2: Graph the function.(make a T table) x -4 -3 y=x2+6x+10 (-4 )2+6(-4)+10=2 (-3 )2+6(-1 ) +10=1 -2 (-2 )2+6(0) +10=2 -1 (-1 )2+6(-1) +10=5 0 (0 )2+6(0)+10=-10 (x,y) (-4,2) (-3,1) (-2,2) (-1,5) (0,10) Step 3: Find the zeros of the related function none Solve the equation by graphing the related function. 2x2 +4x = -3 Step 1: Write the related function. 2x2+ 4x =-3 +3 +3 Hint: Move all terms to one side. 2x2 +4x + 3 = 0 Step 2: Graph the function. (make a T table) Step 3: Find the zeros of the related function No zeros. x -3 y 9 -2 3 -0 1 1 3 2 9 Solve the equation by graphing the related function. 2x2 – 18 = 0 Step 1: Write the related function. y= 2x2 – 18 Step 2: Graph the function.(make a T table) x y=2x2-18 -2 2(-2 )2-18=-10 -1 2(-1 )2-18=-16 0 2(-0 )2-18=-18 1 2(-1 )2-18=-16 2 2(2 )2-18=-10 (x,y) (-2,-10) (-1,-16) (0,-18) (1,-16) (2,-10) Step 3: Find the zeros of the related function -3 and 3 You try: Solve the equation by graphing the related function. x2 – 8x – 16 = 2x2 Step 1: Write the related function. 2- 8x-16=2x2 x -x2+8x+16 -x2+8x+16 0= x2+ 8x +16 x -5 y 1 Hint: Move all terms to one side. You want a positive -4 leading 0 coefficient Step 2: Graph the function. (make a T table) Step 3: Find the zeros of the related function The only zero appears to be -4. -3 1 -2 4 -1 9 Solve the equation by graphing the related function. -12x +18 = -2x2 Step 1: Write the related function. -12x + +2x2 18x=-2x2 +2x2 x 1 Hint: Move all terms to one side. You want a positive leading 2 coefficient 2x2 – 12x + 18 = 0 Step 2: Graph the function. (make a T table) Step 3: Find the zeros of the related function The only zero appears to be 3. y 8 2 3 0 4 2 5 8 Using your graphing calculator: Find the roots of each quadratic polynomial -4 and 5 6) A frog jumps straight up from the ground. The 1) x2-x+20 5 and 7 quadratic function 2 2) x -12x+35 2 + 12t models f(t) = –16t 1 and -2 the frog’s height above 3) x2+x-2 none the ground after t 4) 9x2-6x+2 seconds. About how long 2 is the frog in the air? 2 5) x -4x+4 0 and 0.75 Hint: When the frog leaves the ground, its height is 0, and when the frog lands, its height is 0. So solve 0 = –16t2 + 12t to find the times when the frog leaves the ground and lands. Lesson Quiz Solve each equation by graphing the related function. 1. 3x2 – 12 = 0 2, –2 2. x2 + 2x = 8 –4, 2 3. 3x – 5 = x2 ø 4. 3x2 + 3 = 6x 1 5. A rocket is shot straight up from the ground. The quadratic function f(t) = –16t2 + 96t models the rocket’s height above the ground after t seconds. How long does it take for the rocket to return to the ground? 6 s