* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download An Application of Lie theory to Computer Graphics
Survey
Document related concepts
Transcript
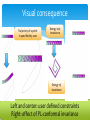
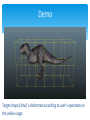
An Application of Lie theory to Computer Graphics Applied Topology 25th July. 2013. Będlewo Shizuo KAJI Yamaguchi University JST/CREST Outline Blend Shape - a problem in CG Mathematical setup Our solution Blend Shape Japanese ex-prime Statue ofminister Moai Mori Blend Shape – The problem Problem: From (two or more) input images, generate interpolated images input: A, B => “(1-t)A + tB”: output Input Output t=0.5 Where is it used ? • • • • • Michael Jackson “Black or White” Movie: Terminator 2、Forest Gump… Creating new industrial design Video compression, High framerate TV Adobe Photoshop/After effects Puppet Warp Igarashi et al. 2005 Beier and Neely 1992 Blend Shape – basic idea input: A, B => “(1-t)A + tB”: output Construct a series of homeos indexed by t ∈ R ft : R2 → R2 t ∈ R It usually requires additional input which should be given manually. (ex. the arrows in the picture) Weakness of classical method desirable What is an appropriate setup for this problem ? Simplicial complex In CG, the most basic representation of geometric object is (triangulated) polyhedron, i.e., simplicial complex 2D 3D Simplicial complex More precisely, ・Abstract simplicial complex (= set of tetrahedra) ・Piecewise Linear (PL) embedding (= vertex positions in Rn) Paraphrase of blend shape Instead of considering objects themselves, ・Consider embeddings from a (reference) simplicial complex ・And find a “suitable” path in the space of embeddings fA/2+B/2 Our algorithm Based on Joint works with K. Anjyo, S. Hirose, H. Ochiai and K. Anjyo, S. Hirose, Y. Mizoguchi, S.Sakata Workflow Problem From given input shapes, generate interpolated shapes input: A, B => “(1-t)A + tB”: output Our strategy is divided into three steps 1. Express input shapes by PL-maps from a reference simplicial complex For each t ∈ R; 2. Construct interpolated affine maps independently for each simplex 3. Assemble those maps into a global PL-immersion 1. Isomorphic subdivision Sub problem Given homeomorphic simplicial complexes, subdivided them to make combinatorially isomorphic Fact: Homeo PL-isomorphic (dimension≦3) There are algorithms to give an explicit isomorphism. But none of them is perfect. This is still an open problem in computational geometry. 1-to-1 We simply rely on existing methods here Assume we have PL-embeddings fA, fB of a reference simplicial complex to the shapes to be blended. We want to find a homotopy Ht connecting fA and fB. H1/2 Ht 2. Local construction First, we consider simplex-wisely Sub problem For each simplex, construct a time varying series of interpolated affine maps, which preserve geometry locally. 2. Local construction More precisely, Sub problem Given two affine maps X and Y, generate a blended affine map At := “(1-t)X + tY” The first guess for the answer would be simply the linear combination of X and Y, but it produces bad results. undesirable desirable 2. Local construction The second guess would be using Lie correspondence Lie algebra Lie group But the problem is the group of affine transformations is not compact. Based on the Cartan decomposition, we have the following surjection, which meets our need. The above map is almost bijective and its continuous inverse ψ can be computed. 2. Local construction Now we can blend affine maps linearly in the parameter space Key points: ・ is not surjective ・There is an explicit and fast computation algorithm for φ, ψ ・The blended map has geometric meaning: for example, the interpolated map stays as close as Euclidean motion (In the sense of Frobenius norm) Nice both geometrically and computationally ! 3. Patching local maps Local to Global Sub problem Assemble the locally constructed affine maps into a global PL-map It is done by finding the minimum of a certain energy functional on the space of PL-immersions. The energy functional : the simplex-wisely blended affine map Key points: * It measures the difference between the PL-map and the locally constructed maps up to PL-conformal equivalence * The minimizer is unique (modulo linear conformal equivalence) and varies smoothly with regard to t Invariant under conformal transformation Users can easily direct the result by adding some terms to it Visual consequence Trajectory of a point Is specified by user Energy w/o invariance Energy w/ invariance Left and center: user defined constraints Right: effect of PL-conformal invariance Applications Our algorithm directly generalizes to more than two inputs input: A, B, C, D… => “sA + tB + uC + vD + …”: output Furthermore, nice properties of our linear parametrization of the affine transformation group allow various applications ・shape deformer (addition/scalar product) ・Inverse kinematics (calculus/differential equation) ・Motion analysis/compression using PCA/ICA (linear algebra) Demo Three shapes are blended according to weights. Weights are specified by user through the “ball controller” Demo Target shape (dino) is deformed according to user’s operation on the yellow cage. Demo Shapes are deformed according to user manipulated handles (invisible) Advertisement There will be a conference on “Math for CG” in October Google “MEIS2013” for detail


































![arXiv:1412.5920v1 [math.CO] 18 Dec 2014](http://s1.studyres.com/store/data/007906890_1-968d1291ae5654c6eb06790a1cfb5c04-150x150.png)

