Download Trigonometry of Non-Right Triangles

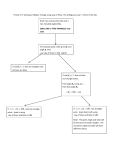
The trigonometry of non-right triangles
So far, we've only dealt with right triangles, but trigonometry can be easily applied to nonright trianglesbecause any non-right triangle can be divided by analtitude* into two right
triangles.
Roll over the triangle to see what that means →
Remember that an altitude is a line segment that has one endpoint at a vertex of a triangle
intersects the opposite side at a right angle. See triangles.
Customary labeling of non-right triangles
This labeling scheme is comßmonly used for non-right triangles. Capital
letters are angles and the corresponding lower-case letters go with the sideopposite the
angle: side a (with length of a units) is across from angle A (with a measure of A degrees or
radians), and so on.
Derivation of the law of sines
Consider the triangle below. if we find the sines of angle Aand angle C using their
corresponding right triangles, we notice that they both contain the altitude, x.
The sine equations are
We can rearrange those by solving each for x (multiply by c on both sides of the left
equation, and by a on both sides of the right):
Now the transitive property says that if both c·sin(A) and a·sin(C) are equal to x, then they
must be equal to each other:
We usually divide both sides by ac to get the easy-to-remember expression of the law of
sines:
We could do the same derivation with the other two altitudes, drawn from angles A and C to
come up with similar relations for the other angle pairs. We call these together the law of
sines. It's in the green box below.
The law of sines can be used to find the measure of an angle or a side of a non-right
triangle if we know:
•
•
two sides and an angle not between them or
two angles and a side not between them.
Law of Sines
Examples: Law of sines
Use the law of sines to find the missing measurements of the triangles in these examples.
In the first, two angles and a side are known. In the second two sides and an angle. Notice
that we need to know at least one angle-opposite side pair for the Law of Sines to work.
Example 1
Find all of the missing measurements of this triangle:
The missing angle is easy, it's just
Now set up one of the law of sines proportions and solve for the missing piece, in this case
the length of the lower side:
Then do the same for the other missing side. It's best to use the original known angle and
side so that round-off errors or mistakes don't add up.
Example 2
Find all of the missing measurements of this triangle:
First, set up one law of sines proportion. This time we'll be solving for a missing angle, so
we'll have to calculate aninverse sine:
Now it's easy to calculate the third angle:
Then apply the law of sines again for the missing side. We have two choices, we can solve
Either gives the same answer,
Derivation of the law of cosines
Consider another non-right triangle, labeled as shown with side lengths x and y. We can
derive a useful law containing only the cosine function.
First use the Pythagorean theorem to derive two equations for each of the right triangles:
Notice that each contains and x2, so we can eliminate x2between the two using the transitive
property:
Then expand the binomial (b - y)2 to get the equation below, and note that the y2 cancel:
Now we still have a y hanging around, but we can get rid of it using the cosine solution,
notice that
Substituting c·cos(A) for y, we get
which is the law of cosines
The law of cosines can be used to find the measure of an angle or a side of a non-right
triangle if we know:
•
•
two sides and the angle between them or
three sides and no angles.
We could again do the same derivation using the other two altitudes of our triangle, to yield
three versions of the law of cosines for any triangle. They are listed in the box below.
Law of Cosines
The Law of Cosines is just the Pythagorean relationship with a correction factor, e.g.2bc·cos(A), to account for the fact that the triangle is not a right triangle. We can write three
versions of the LOC, one for every angle/opposite side pair:
Examples: Law of cosines
Use the law of cosines to find the missing measurements of the triangles in these two
examples. In the first, the measures of two sides and the included angle (the angle between
them) are known. In the second, three sides are known.
Example 3
Find all of the missing measurements of this triangle:
Set up the law of cosines using the only set of angles and sides for which it is possible in
this case:
Now using the new side, find one of the missing angles using the law of sines:
And then the third angle is
In general, try to use the law of sines first. It's easier and less prone to errors. But in this
case, that wasn't possible, so the law of cosines was necessary.
Example 4
Find all of the missing measurements of this triangle:
Set up the law of cosines to solve for either one of the angles:
Rearrange to solve for A. You'll need an inverse cosine to get the angle.
Use the law of sines to find a second angle
Finally, just calculate the third angle:
Practice problems
Find the measures of all missing sides and angles of these triangles:
(Hint: Always use the LOS first if you can. It's simpler. When that fails, use the LOC, but
then you can usually use other means to fill in the rest of the measurements.)
Download solutions