Download Analysis of Algorithms

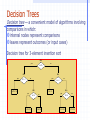
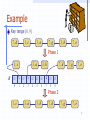
Sorting and Selection
1, c
B 
3, a

3, b
  
7, d
7, g
7, e
 
0 1 2 3 4 5 6 7 8 9
1
Lower Bounds
Lower bound: an estimate on a minimum amount
of work needed to solve a given problem
Examples:
number of comparisons needed to find the
largest element in a set of n numbers
number of comparisons needed to sort an array
of size n
number of comparisons necessary for
searching in a sorted array
Lower Bounds (cont.)
Lower bound can be


an exact count
an efficiency class ()
Tight lower bound: there exists an algorithm
with the same efficiency as the lower bound
Problem
sorting (comparison-based)
searching in a sorted array
element uniqueness
n-digit integer multiplication
multiplication of n-by-n matrices
Lower bound Tightness
(nlog n)
(log n)
(nlog n)
(n)
(n2)
yes
yes
yes
unknown
unknown
Decision Trees
Decision tree — a convenient model of algorithms involving
comparisons in which:
 internal nodes represent comparisons
 leaves represent outcomes (or input cases)
Decision tree for 3-element insertion sort
abc
yes
a<b
no
abc
yes
bac
no
b< c
yes
acb
a<b<c
yes
a<c<b
a<c
no
a<c
bca
b<a<c
no
c<a<b
yes
b<c<a
b<c
no
c<b<a
Decision Trees and Sorting Algorithms
Any comparison-based sorting algorithm can be
represented by a decision tree (for each fixed n)
Number of leaves (outcomes)  n!
Height of binary tree with n! leaves  log2n!
Minimum number of comparisons in the worst case 
log2n! for any comparison-based sorting algorithm, since
the longest path represents the worst case and its length
is the height
log2n!  n log2n (by Sterling approximation)
This lower bound is tight (mergesort or heapsort)
Ex. Prove that 5 (or 7) comparisons are necessary and sufficient for
sorting 4 keys (or 5 keys, respectively).
Bucket-Sort
Let be S be a sequence of n
(key, element) items with keys
in the range [0, N - 1]
Bucket-sort uses the keys as
indices into an auxiliary array B
of sequences (buckets)
Phase 1: Empty sequence S by
moving each item (k, o) into its
bucket B[k]
Phase 2: For i = 0, …, N - 1, move
the items of bucket B[i] to the
end of sequence S
Analysis:


Phase 1 takes O(n) time
Phase 2 takes O(n + N) time
Bucket-sort takes O(n + N) time
Algorithm bucketSort(S, N)
Input sequence S of (key, element)
items with keys in the range
[0, N - 1]
Output sequence S sorted by
increasing keys
B  array of N empty sequences
while S.isEmpty()
f  S.first()
(k, o)  S.remove(f)
B[k].insertLast((k, o))
for i  0 to N - 1
while B[i].isEmpty()
f  B[i].first()
(k, o)  B[i].remove(f)
S.insertLast((k, o))
6
Example
Key range [0, 9]
7, d
1, c
3, a
7, g
3, b
7, e
Phase 1
1, c
B
3, a

0

1
2
3
3, b



4
5
6
7
7, d


8
9
7, g
7, e
Phase 2
1, c
3, a
3, b
7, d
7, g
7, e
7
Properties and Extensions
Key-type Property


The keys are used as
indices into an array
and cannot be arbitrary
objects
No external comparator
Stable Sort Property

The relative order of
any two items with the
same key is preserved
after the execution of
the algorithm
Extensions

Integer keys in the range [a, b]
 Put item (k, o) into bucket
B[k - a]

String keys from a set D of
possible strings, where D has
constant size (e.g., names of
the 50 U.S. states)
 Sort D and compute the rank
r(k) of each string k of D in
the sorted sequence
 Put item (k, o) into bucket
B[r(k)]
8
Lexicographic Order
A d-tuple is a sequence of d keys (k1, k2, …, kd), where
key ki is said to be the i-th dimension of the tuple
Example:

The Cartesian coordinates of a point in space are a 3-tuple
The lexicographic order of two d-tuples is recursively
defined as follows
(x1, x2, …, xd) < (y1, y2, …, yd)

x1 < y1  x1 = y1  (x2, …, xd) < (y2, …, yd)
I.e., the tuples are compared by the first dimension,
then by the second dimension, etc.
9
Lexicographic-Sort
Let Ci be the comparator
that compares two tuples by
their i-th dimension
Let stableSort(S, C) be a
stable sorting algorithm that
uses comparator C
Lexicographic-sort sorts a
sequence of d-tuples in
lexicographic order by
executing d times algorithm
stableSort, one per
dimension
Lexicographic-sort runs in
O(dT(n)) time, where T(n) is
the running time of
stableSort
Algorithm lexicographicSort(S)
Input sequence S of d-tuples
Output sequence S sorted in
lexicographic order
for i  d downto 1
stableSort(S, Ci)
Example:
(7,4,6) (5,1,5) (2,4,6) (2, 1, 4) (3, 2, 4)
(2, 1, 4) (3, 2, 4) (5,1,5) (7,4,6) (2,4,6)
(2, 1, 4) (5,1,5) (3, 2, 4) (7,4,6) (2,4,6)
(2, 1, 4) (2,4,6) (3, 2, 4) (5,1,5) (7,4,6)
10
Radix-Sort
Radix-sort is a
specialization of
lexicographic-sort that
uses bucket-sort as the
stable sorting algorithm
in each dimension
Radix-sort is applicable
to tuples where the
keys in each dimension i
are integers in the
range [0, N - 1]
Radix-sort runs in time
O(d( n + N))
Algorithm radixSort(S, N)
Input sequence S of d-tuples such
that (0, …, 0)  (x1, …, xd) and
(x1, …, xd)  (N - 1, …, N - 1)
for each tuple (x1, …, xd) in S
Output sequence S sorted in
lexicographic order
for i  d downto 1
bucketSort(S, N)
11
Radix-Sort for
Binary Numbers
Consider a sequence of n
b-bit integers
x = xb - 1 … x1x0
We represent each element
as a b-tuple of integers in
the range [0, 1] and apply
radix-sort with N = 2
This application of the
radix-sort algorithm runs in
O(bn) time
For example, we can sort a
sequence of 32-bit integers
in linear time
Algorithm binaryRadixSort(S)
Input sequence S of b-bit
integers
Output sequence S sorted
replace each element x
of S with the item (0, x)
for i  0 to b - 1
replace the key k of
each item (k, x) of S
with bit xi of x
bucketSort(S, 2)
12
Example
Sorting a sequence of 4-bit integers
1001
0010
1001
1001
0001
0010
1110
1101
0001
0010
1101
1001
0001
0010
1001
0001
1101
0010
1101
1101
1110
0001
1110
1110
1110
13
Order Statistics
The ith order statistic in a set of n elements is
the ith smallest element
The minimum is thus the 1st order statistic
The maximum is (duh) the nth order statistic
The median is the n/2 order statistic

If n is even, there are 2 medians
Could calculate order statistics by sorting


Time: O(n lg n) w/ comparison sort
We can do better
Selection Problem
The selection problem: find the ith
smallest element of a set
Two algorithms:


A practical randomized algorithm with O(n)
expected running time
A cool algorithm of theoretical interest only
with O(n) worst-case running time
Randomized Selection
Key idea: use partition() from quicksort


But, only need to examine one subarray
This saving shows up in running time: O(n)
 A[q]
p
 A[q]
q
r
Randomized Selection
RandomizedSelect(A, p, r, i)
if (p == r) then return A[p];
q = RandomizedPartition(A, p, r)
k = q - p + 1;
if (i == k) then return A[q];
if (i < k) then
return RandomizedSelect(A, p, q-1, i);
else
return RandomizedSelect(A, q+1, r, i-k);
k
 A[q]
p
 A[q]
q
r
Review: Randomized Selection
Average case

For upper bound, assume ith element always falls
in larger side of partition:
T n  


1 n -1
T max k , n - k - 1 + n 

n k =0
2 n -1
T k  + n 

n k =n / 2
We then showed that T(n) = O(n) by substitution
Linear-Time Median Selection
Given a “black box” O(n) median algorithm,
what can we do?
 ith order statistic:
 Find median x
 Partition input around x
 if (i  (n+1)/2) recursively find ith element of
first half
 else find (i - (n+1)/2)th element in second half
 T(n) = T(n/2) + O(n) = O(n)

Can you think of an application to sorting?
Linear-Time Median Selection
Worst-case O(n lg n) quicksort



Find median x and partition around it
Recursively quicksort two halves
T(n) = 2T(n/2) + O(n) = O(n lg n)