* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Confidence Intervals – Introduction
Survey
Document related concepts
Transcript
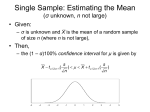
Confidence Intervals – Introduction • A point estimate provides no information about the precision and reliability of estimation. • For example, the sample mean X is a point estimate of the population mean μ but because of sampling variability, it is virtually never the case that x . • A point estimate says nothing about how close it might be to μ. • An alternative to reporting a single sensible value for the parameter being estimated it to calculate and report an entire interval of plausible values – a confidence interval (CI). 1 Confidence level • A confidence level is a measure of the degree of reliability of a confidence interval. It is denoted as 100(1-α)%. • The most frequently used confidence levels are 90%, 95% and 99%. • A confidence level of 100(1-α)% implies that 100(1-α)% of all samples would include the true value of the parameter estimated. • The higher the confidence level, the more strongly we believe that the true value of the parameter being estimated lies within the interval. week 5 2 CI for μ When σ is Known • Suppose X1, X2,…,Xn are random sample from N(μ, σ2) where μ is unknown and σ is known. • A 100(1-α)% confidence interval for μ is, x z 2 n • Proof: week 5 3 Example • The National Student Loan Survey collected data about the amount of money that borrowers owe. The survey selected a random sample of 1280 borrowers who began repayment of their loans between four to six months prior to the study. The mean debt for the selected borrowers was $18,900 and the standard deviation was $49,000. Find a 95% for the mean debt for all borrowers. week 5 4 Width and Precision of CI • The precision of an interval is conveyed by the width of the interval. • If the confidence level is high and the resulting interval is quite narrow, the interval is more precise, i.e., our knowledge of the value of the parameter is reasonably precise. • A very wide CI implies that there is a great deal of uncertainty concerning the value of the parameter we are estimating. • The width of the CI for μ is …. week 5 5 Important Comment • Confidence intervals do not need to be central, any a and b that solve X P a b 1 / n define 100(1-α)% CI for the population mean μ. week 5 6 One Sided CI • CI gives both lower and upper bounds for the parameter being estimated. • In some circumstances, an investigator will want only one of these two types of bound. • A large sample upper confidence bound for μ is x z n • A large sample lower confidence bound for μ is x z n week 5 7 CI for μ When σ is Unknown • Suppose X1, X2,…,Xn are random sample from N(μ, σ2) where both μ and σ are unknown. • If σ2 is unknown we can estimate it using s2 and use the tn-1 distribution. • A 100(1-α)% confidence interval for μ in this case, is … week 5 8 Large Sample CI for μ • Recall: if the sample size is large, then the CLT applies and we have X / n d Z ~ N 0,1. • A 100(1-α)% confidence interval for μ, from a large iid sample is x z n 2 • If σ2 is not known we estimate it with s2. week 5 9 Example – Binomial Distribution • Suppose X1, X2,…,Xn are random sample from Bernoulli(θ) distribution. A 100(1-α)% CI for θ is…. • Example… week 5 10