Download some extra notes on this

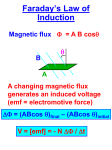
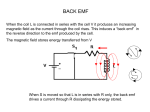
The section of the course on inductors, AC, and transformers: a quick review.
(Check out the lecture notes, of course) Here's what I would say is the big picture:
Faraday's law says EMF = - d (Flux) / dt. This is the "big idea", one of Maxwell's
equations and one of the greatest physics discoveries in all of history. This equation has
LOTS of practical consequences, and the section of the course on inductors and
transformers is just a small part of this.
In words the equation says: if you try to change the magnetic field throughout some
region of space (that's a change in flux, which is just B-field * area) then you will induce
a voltage, or EMF, in "rings" around that region. If there is a metal ring physically
present, this voltage will make current flow around the ring. So... changing magnetic
fields CREATES electric fields and therefore currents. This is how we create currents in
practice - the power company has some big metal coil, they change the magnetic flux
through it (probably by rotating the ring) and this makes current flow. That's the physical
source of electrical current to your house!
The minus sign in the equation is Lenz' law, by the way: the EMF is oriented to try to
"fight the change". How? Well, if current flows around any ring, that creates its own little
magnetic field, and the sign says this new (induced) magnetic field will point in just such
a way as to oppose the change in the original, external magnetic field.
So what's induction? It's the generic name for any situation where you have two coils
which are near one another. Flowing current in ONE coil makes a B field, and the other
coil then "picks up" some of that B field, and (because of Faraday's law!) current flows in
IT to try to "fight the change". So changing current in one coil creates a changing current
in the other one. That's called "mutual inductance" (or "a transformer", see below)
This can happen with a SINGLE coil - if you try to run current through any loop, it
creates its own B field. If that current is changing, then Faraday's law says a new EMF
gets induced which fights the change. That's called "self inductance", and we simple refer
to any coil as an "inductor". So the big idea here is that when you twist metal into loops,
and then try to run current through the metal, even if there is no (Ohmic) resistance, there
will be a new *kind* of resistance. It's different than Ohm's law - it doesn't persist, it just
resists the CHANGE in current.
The formula here (derived in the lecture notes - you know where to find those, right? See
the web page!) is EMF = -L dI/dt. The "L" is a constant, the "inductance" of the loop. It
is measured in "Henry's" in the SI metric system, and the bigger it is, the more the loop
hates/resists change. You can COMPUTE L for a perfect, long coil (a "solenoid"),
otherwise you might just measure it. "I" here is the current flowing through the coil. EMF
is just voltage - so an inductor is a circuit element which fights change in current. It is
denoted by the little springy coil symbol. There will be a voltage difference across it
when you put it in a circut, which is NOT "IR" (like Ohm's law), it doesn't matter what
the current is... it matters how rapidly the current is changing.
So in circuits, the rules for inductors are pretty simple: after a long time (when everything
has settled down), there is no CHANGE in time, so therefore no EMF across inductors.
That means they look like ordinary ideal wires. (They ARE, after all, ordinary ideal
wires, just coiled up!) They act like a "short". But if you now try to CHANGE the current
(by doing something somewhere else in the circuit), the inductor will not let this happen
instantly. It takes time. For the first instant when you're trying to change current, the
inductor insists that current flow stays the same. If it started with no current, then it looks
like a broken wire. (But if it started WITH current, then it does NOT look like that! By
hook or by crook, current will continue to flow. This was the scene from "the Thing",
where they tried to open a switch which had had a lot of current flowing through it. They
open the switch, but there must've been a big inductor in the circuit, because current
briefly CONTINUES to flow even though you opened a switch. How can that happen? A
spark developes to force the current to keep flowing)
You can imagine all sorts of nice uses for inductors. They "smooth" things out
electrically, preventing sudden changes in current. (When teamed up with capacitors, all
SORTS of cool effects can happen, but we didn't have a chance to cover this!)
A transformer is basically what you get when you have TWO loops next to each other.
This is what I mentioned above - changing current in one of them induces a current in the
other. We call this the "primary and secondary" coils. The lecture notes derive the
relation between voltages (EMF's) across the two coils - it's just the ratio of the number
of turns of each coil (assuming that otherwise all the magnetic field lines that pass
through one also pass through the other - i.e. that they are "tightly coupled") The
usefulness of transformers is visible everywhere - this is how you change high voltage
(120 V) from the wall into low voltage (a few volts) to charge your computer or cell
phone. That little black charging box has two coils of wire in it - one connected to the
wall, the other connects to the "output". One of the key points here was to notice that
power goes into one coil (Power = V*I) and so power must go out the other, that's just
conservation of energy. If everything is ideal, they'll be exactly equal. So if the voltage
across one coil is HIGHER, the current is SMALLER, and vice-versa. (This is useful for
charging your cell phone - you step the voltage way DOWN so as not to fry your little
low voltage battery, but this also means you step the current way UP so it charges that
much faster. Nice!)
The last part of this story was AC. When you have a coil rotating in a magnetic field, the
"flux" through the coil changes smoothly. Since flux = BA cos(theta) (where theta is the
angle between the field and the normal of the coil), then if theta is changing steadily
(theta = constant*time) then the flux is changing sinusoidally with time. And changing
flux means (by Faraday) an EMF. Here, you just take the derivative, and find that the
resulting voltage (and thus current) around that loop is just sinusoidal. It "alternates",
positive to negative, that's alternating current (or AC). That's what the rotating coil at the
power plant generates, and it connects straight to your house. So the wall sockets have a
voltage which looks like V0 sin(omega*t). V0 is the "peak voltage" (because sin goes up
to 1) and omega is the "angular frequency", it's just 2pi * regular frequency, (where
regular frequency is measured in cycles/second, or Hz) If you hook the plug up to a
simple circuit (like a light bulb, or toaster) then the current flowing is just I = V/R, and R
is probably constant, so the current is also alternating, I = I0 sin(omega*t). (I0 = V0/R, in
this simple case). Now if current oscillates, technically the average current would be zero.
But that is not so physically meaningful - I mean, current oscillating back and forth
through a bulb still lights it up! So we think about power = V*I, and then we have a
sin^2(omega*t), and sin^2 does NOT average to zero, it averages to ½. So this leads us to
define the "rms" (root mean square) voltage, V(rms) = V0/Sqrt[2]. (It's defined so that
V(rms)^2 = V0^2/2, which is just the AVERAGE of the square of the true voltage).
V(rms) is handy because you can "pretend" you have a regular old battery circuit like we
covered earlier in the term, just talk about "rms" everything (voltage, current, average
power) and you can use all the old equations, like V(rms) = I(rms)*R, or average power
= V(rms)*I(rms) = V(rms)^2/R = I(rms)^2 * R. Just like we used to do.
I think those were the big ideas:
Faraday's law leads to inductors and transformers, (and all of these are most interesting
when you have varying currents, like AC...)
You should be able to:
Look at a simple circuit with batteries, R's, and L's and figure out what happens "just
before" and "just after" and "long after" you make a change.
Compute voltage and current and power in primary and secondary of transformers, and
connect this to the number of coils. (Knowing the field in a solenoid is very helpful here)
Understand and use (rms) and (peak) and (average) properly in simple situations with
AC.
Figure out the direction of current flow (i.e. Lenz' law) when you make some changes in
something (like ramping current up or down), or, if there's no wire there - figure out the
direction of induced electric field. This last point comes from interpreting "EMF" as "the
integral of E dot dL", which goes back to the very original days when we studied voltage!
So, you can think about Faraday's law as "inducing voltage around a ring", but
equivalently you can think about it as inducing electric fields which run in circular
patterns.