* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download some extra notes on this
Wireless power transfer wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Stepper motor wikipedia , lookup
Mercury-arc valve wikipedia , lookup
Brushed DC electric motor wikipedia , lookup
Skin effect wikipedia , lookup
Power engineering wikipedia , lookup
Electrical substation wikipedia , lookup
Three-phase electric power wikipedia , lookup
Electrical ballast wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Transformer wikipedia , lookup
Voltage regulator wikipedia , lookup
Voltage optimisation wikipedia , lookup
Electric machine wikipedia , lookup
History of electric power transmission wikipedia , lookup
Ignition system wikipedia , lookup
Transformer types wikipedia , lookup
Opto-isolator wikipedia , lookup
Surge protector wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Current source wikipedia , lookup
Stray voltage wikipedia , lookup
Magnetic core wikipedia , lookup
Mains electricity wikipedia , lookup
Buck converter wikipedia , lookup
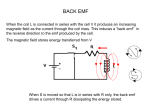
The section of the course on inductors, AC, and transformers: a quick review. (Check out the lecture notes, of course) Here's what I would say is the big picture: Faraday's law says EMF = - d (Flux) / dt. This is the "big idea", one of Maxwell's equations and one of the greatest physics discoveries in all of history. This equation has LOTS of practical consequences, and the section of the course on inductors and transformers is just a small part of this. In words the equation says: if you try to change the magnetic field throughout some region of space (that's a change in flux, which is just B-field * area) then you will induce a voltage, or EMF, in "rings" around that region. If there is a metal ring physically present, this voltage will make current flow around the ring. So... changing magnetic fields CREATES electric fields and therefore currents. This is how we create currents in practice - the power company has some big metal coil, they change the magnetic flux through it (probably by rotating the ring) and this makes current flow. That's the physical source of electrical current to your house! The minus sign in the equation is Lenz' law, by the way: the EMF is oriented to try to "fight the change". How? Well, if current flows around any ring, that creates its own little magnetic field, and the sign says this new (induced) magnetic field will point in just such a way as to oppose the change in the original, external magnetic field. So what's induction? It's the generic name for any situation where you have two coils which are near one another. Flowing current in ONE coil makes a B field, and the other coil then "picks up" some of that B field, and (because of Faraday's law!) current flows in IT to try to "fight the change". So changing current in one coil creates a changing current in the other one. That's called "mutual inductance" (or "a transformer", see below) This can happen with a SINGLE coil - if you try to run current through any loop, it creates its own B field. If that current is changing, then Faraday's law says a new EMF gets induced which fights the change. That's called "self inductance", and we simple refer to any coil as an "inductor". So the big idea here is that when you twist metal into loops, and then try to run current through the metal, even if there is no (Ohmic) resistance, there will be a new *kind* of resistance. It's different than Ohm's law - it doesn't persist, it just resists the CHANGE in current. The formula here (derived in the lecture notes - you know where to find those, right? See the web page!) is EMF = -L dI/dt. The "L" is a constant, the "inductance" of the loop. It is measured in "Henry's" in the SI metric system, and the bigger it is, the more the loop hates/resists change. You can COMPUTE L for a perfect, long coil (a "solenoid"), otherwise you might just measure it. "I" here is the current flowing through the coil. EMF is just voltage - so an inductor is a circuit element which fights change in current. It is denoted by the little springy coil symbol. There will be a voltage difference across it when you put it in a circut, which is NOT "IR" (like Ohm's law), it doesn't matter what the current is... it matters how rapidly the current is changing. So in circuits, the rules for inductors are pretty simple: after a long time (when everything has settled down), there is no CHANGE in time, so therefore no EMF across inductors. That means they look like ordinary ideal wires. (They ARE, after all, ordinary ideal wires, just coiled up!) They act like a "short". But if you now try to CHANGE the current (by doing something somewhere else in the circuit), the inductor will not let this happen instantly. It takes time. For the first instant when you're trying to change current, the inductor insists that current flow stays the same. If it started with no current, then it looks like a broken wire. (But if it started WITH current, then it does NOT look like that! By hook or by crook, current will continue to flow. This was the scene from "the Thing", where they tried to open a switch which had had a lot of current flowing through it. They open the switch, but there must've been a big inductor in the circuit, because current briefly CONTINUES to flow even though you opened a switch. How can that happen? A spark developes to force the current to keep flowing) You can imagine all sorts of nice uses for inductors. They "smooth" things out electrically, preventing sudden changes in current. (When teamed up with capacitors, all SORTS of cool effects can happen, but we didn't have a chance to cover this!) A transformer is basically what you get when you have TWO loops next to each other. This is what I mentioned above - changing current in one of them induces a current in the other. We call this the "primary and secondary" coils. The lecture notes derive the relation between voltages (EMF's) across the two coils - it's just the ratio of the number of turns of each coil (assuming that otherwise all the magnetic field lines that pass through one also pass through the other - i.e. that they are "tightly coupled") The usefulness of transformers is visible everywhere - this is how you change high voltage (120 V) from the wall into low voltage (a few volts) to charge your computer or cell phone. That little black charging box has two coils of wire in it - one connected to the wall, the other connects to the "output". One of the key points here was to notice that power goes into one coil (Power = V*I) and so power must go out the other, that's just conservation of energy. If everything is ideal, they'll be exactly equal. So if the voltage across one coil is HIGHER, the current is SMALLER, and vice-versa. (This is useful for charging your cell phone - you step the voltage way DOWN so as not to fry your little low voltage battery, but this also means you step the current way UP so it charges that much faster. Nice!) The last part of this story was AC. When you have a coil rotating in a magnetic field, the "flux" through the coil changes smoothly. Since flux = BA cos(theta) (where theta is the angle between the field and the normal of the coil), then if theta is changing steadily (theta = constant*time) then the flux is changing sinusoidally with time. And changing flux means (by Faraday) an EMF. Here, you just take the derivative, and find that the resulting voltage (and thus current) around that loop is just sinusoidal. It "alternates", positive to negative, that's alternating current (or AC). That's what the rotating coil at the power plant generates, and it connects straight to your house. So the wall sockets have a voltage which looks like V0 sin(omega*t). V0 is the "peak voltage" (because sin goes up to 1) and omega is the "angular frequency", it's just 2pi * regular frequency, (where regular frequency is measured in cycles/second, or Hz) If you hook the plug up to a simple circuit (like a light bulb, or toaster) then the current flowing is just I = V/R, and R is probably constant, so the current is also alternating, I = I0 sin(omega*t). (I0 = V0/R, in this simple case). Now if current oscillates, technically the average current would be zero. But that is not so physically meaningful - I mean, current oscillating back and forth through a bulb still lights it up! So we think about power = V*I, and then we have a sin^2(omega*t), and sin^2 does NOT average to zero, it averages to ½. So this leads us to define the "rms" (root mean square) voltage, V(rms) = V0/Sqrt[2]. (It's defined so that V(rms)^2 = V0^2/2, which is just the AVERAGE of the square of the true voltage). V(rms) is handy because you can "pretend" you have a regular old battery circuit like we covered earlier in the term, just talk about "rms" everything (voltage, current, average power) and you can use all the old equations, like V(rms) = I(rms)*R, or average power = V(rms)*I(rms) = V(rms)^2/R = I(rms)^2 * R. Just like we used to do. I think those were the big ideas: Faraday's law leads to inductors and transformers, (and all of these are most interesting when you have varying currents, like AC...) You should be able to: Look at a simple circuit with batteries, R's, and L's and figure out what happens "just before" and "just after" and "long after" you make a change. Compute voltage and current and power in primary and secondary of transformers, and connect this to the number of coils. (Knowing the field in a solenoid is very helpful here) Understand and use (rms) and (peak) and (average) properly in simple situations with AC. Figure out the direction of current flow (i.e. Lenz' law) when you make some changes in something (like ramping current up or down), or, if there's no wire there - figure out the direction of induced electric field. This last point comes from interpreting "EMF" as "the integral of E dot dL", which goes back to the very original days when we studied voltage! So, you can think about Faraday's law as "inducing voltage around a ring", but equivalently you can think about it as inducing electric fields which run in circular patterns.