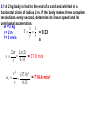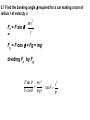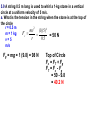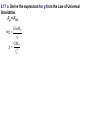Download PowerPoint Presentation - Mr. Cervantes Science Classes

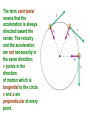
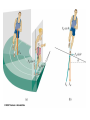
UNIFORM CIRCULAR MOTION
Uniform circular motion is motion in which there is no
change in speed, only a change in direction.
CENTRIPETAL ACCELERATION
An object experiencing uniform
circular motion is continually
accelerating. The position and
velocity of a particle moving in a
circular path of radius r are
shown at two instants in the
figure.
When the particle is at
point A, its velocity is
represented by vector v1.
After a time interval t, its
velocity is represented by
the vector v2.
The acceleration is given
by:v s chord
v

R

v v2  v1
a

t
t
radius
as Δt becomes smaller and smaller, the chord
length becomes equal to the arc length s = v
Δt
 v v t

v
R
v v 2

t
R
The term centripetal
means that the
acceleration is always
directed toward the
center. The velocity
and the acceleration
are not necessarily in
the same direction;
v points in the
direction
of motion which is
tangential to the circle.
v and a are
perpendicular at every
point.
The period T is the time for one complete revolution. So
the linear speed can be found by dividing the period into
the circumference:
2r
v
T
Units: m/s
Another useful parameter in engineering problems is the
rotational speed, expressed in revolutions per minute
(rpm) or revolutions per second (rev/s). This quantity is
called the frequency f of rotation and is given by the
reciprocal of the period.
1
f 
T
Units: s1
5.1 A 2 kg body is tied to the end of a cord and whirled in a
horizontal circle of radius 2 m. If the body makes three complete
revolutions every second, determine its linear speed and its
centripetal
m = 2 kg acceleration.
r=2m
f = 3 rev/s
1 1
T 
= 0.33
f 3
s
2r 2 ( 2)

v
= 37.8 m/s
0.33
t
v 2 (37.8) 2
ac 
= 714.4 m/s2

r
0.33
5.2 A ball is whirled at the end of a string in a horizontal circle 60
cm in radius at the rate of 1 revolution every 2 s. Find the ball's
centripetal acceleration.
r = 0.6 m
f = 1 rev/2 s
t=2s
v 2 (2r / t ) 2
ac 

r
r
4 2 r 4 2 (0.6)
2
=
5.92
m/s
 2 
22
t
CENTRIPETAL FORCE
The inward force necessary to maintain uniform circular
motion is defined as centripetal force. From Newton's
Second Law, the centripetal force is given by:
2
mv
Fc 
r
5.3 Two 4 N weights rotate about a center axis 3 m long at 12 rev/s,.
a. What is the resultant force acting on each weight?
Fg = 4 N
f = 12 rev/ s
v = 2πrf
=2π (1.5)(12)
= 113 m/s
mv 2 (4 / 9.8)(113) 2

Fc 
= 3474 N
1.5
r
b. What is the tension in the rod?
The resultant force on each mass is equal to 3474 N
directed toward the center. It is exerted by the center rod
on the mass. The outward force we often think acts on
the mass is actually the reaction force exerted by the
mass on the rod. The tension in the rod is due to this
outward force, and it is equal in magnitude to the
centripetal force of 3474 N.
The Forbidden F-Word
When the subject of circular motion is discussed, it is
not uncommon to hear mention of the word
"centrifugal." Centrifugal, not to be confused with
centripetal, means away from the center or outward.
The use of or at least the familiarity with this word
centrifugal, combined with the common sensation of
an outward force when experiencing circular motion,
often creates or reinforces a deadly student
misconception. The deadly misconception, is the
notion that objects in circular motion are experiencing
an outward force. "After all," a well-meaning student
may think, "I can recall vividly the sensation of being
thrown outward away from the center of the circle on
that roller coaster ride. Therefore, circular motion must
be characterized by an outward force."
Centrifugal Force is often used to describe why mud gets
spun off a spinning tire, or water gets pushed out of the
clothes during the spin dry cycle of your washer. It is also
used to describe why we tend to slide to the outer side of a
car going around a curve.
Let’s imagine that you are riding in a car going around a
curve. Sitting on your dashboard is a cassette tape. As you
go around the curve, the tape moves to outside edge of the
car. Because you don't want to blame it on ghosts, you say
"centrifugal force pushed the tape across the dashboard.“
Wwrroonngg!!
When we view this situation from above the car, we get a
better view of what is really happening. The animation
shows both views at the same time. The top window shows
you the passenger's view of the car and the tape, while the
bottom window shows you the bird's eye view.
There is enough static friction on the sides of the tires to act
as centripetal force which forces the car to stay in the
circular path.
The tape on the slippery dashboard does not have enough
friction to act as a centripetal force, so in the absence of a
centripetal force the tape follows straight line motion. The
car literally turns out from underneath the tape, but from the
passenger's point of view it looks as though something (a
ghost force?) pushed the tape across the dashboard. If the
car you are riding in has the windows rolled down, then the
tape will leave the car (or does the car leave the tape?) as it
follows its straight line path. If the windows are rolled up,
then the window will deliver a centripetal force to the tape
and keep it in a circular path.
Without a centripetal
force, an object in
motion continues along a
straight-line path.
With a centripetal force,
an object in motion will
be accelerated and
change its direction.
5.4 A 1000-kg car rounds a turn of radius 30 m at a velocity of 9 m/s
a. How much centripetal force is required?
m = 1000 kg
r = 30 m
v = 9 m/s
mv 2 (1000)(9) 2
Fc 

= 2700
30
r
N
b. Where does this force come from?
Force of friction between tires and
road.
When an automobile is driven around a sharp turn on a
perfectly level road, friction between the tires and the
road provides the centripetal force. If this force is not
adequate, the car may slide off the road.
The maximum value
of the force of
friction determines
the maximum
speed with which a
car can negotiate a
turn of a given
radius.
5.5 The maximum force a road can exert on the tires of a 1500-kg
car is 8500 N. What is the maximum velocity at which the car can
round a turn of radius 120 m?
m = 1500 kg
F = 8500 N
r = 120 m
v
mv 2
Fc 
r
Fr
8500(120)

= 26 m/s (94 km/h)
1500
m
5.6 A car is traveling at 20 km/h on a level road where the
coefficient of static friction between tires and road is 0.8. Find the
minimum turning radius of the car.
v = 5.55
m/s
μ = 0.8
Fc = Ff
mv 2
  s mg
r
(5.55) 2
v2

r
= 3.93 m
 s g 0.8(9.8)
If we consider the effects of banking a turn to eliminate
the friction force we observe that the horizontal
component of the normal force provides the necessary
centripetal force.
5.7 Find the banking angle  required for a car making a turn of
radius r at velocity v.
mv 2
Fx = F sin 
r
=
Fy = F cos  = Fg = mg
dividing Fx by Fg
F sin  mv 2

F cos  mgr
v2
tan  
gr
The proper banking angle  depends only on v and r, not
on the mass of the car. If a car goes around a banked
turn more slowly than at the design velocity, friction
tends to keep it from sliding down the inclined roadway;
if the car goes faster, friction tends to keep it from
skidding outward.
If the car's
speed is too
great, however,
friction may not
be sufficient to
keep the car on
the road.
5.8 a. Find the required banking angle for a curve of radius 300 m if
the curve is to be negotiated at a speed of 80 km/h.
r = 300 m
v = 22.2 m/s
v2
tan  
gr
 (22.2) 2 
 = 9.5˚
  tan 
 9.8(300) 
1
b. If the curve were not banked, what coefficient of friction would
be required between the tires and the road?
From problem 5.6
v2
r
s g
v 2 (22.2) 2
s 

= 0.17
rg 9.8(300)
MOTION IN A VERTICAL
CIRCLE
When a body moves in a
vertical circle at the end of a
string, the tension FT in the
string varies with the body's
position. The centripetal
force Fc on the body at any
point is the vector sum of FT
and the component of the
body's weight toward the
center of the circle.
The figure shows the forces
exerted on an airplane at the
upper and lower limits of a
vertical loop.
At the highest point in the
circular turn the
centripetal
force is given by:2
mv
F1  mg 
R
When the aircraft
passes
through the lowest
point
in the loop the 2
mv
centripetal
F2  mg 
R
force is:
5.9 A string 0.5 m long is used to whirl a 1-kg stone in a vertical
circle at a uniform velocity of 5 m/s.
a. What is the tension in the string when the stone is at the top of
the circle
r = 0.5 m
mv 2 (1)(5) 2
m = 1 kg
Fc 

= 50 N
0. 5
r
v=5
m/s
Fg = mg = 1 (9.8) = 98 N
Top of Circle
Fc = FT + Fg
FT = Fc - Fg
= 50 - 9.8
= 40.2 N
b. What is the tension in the string when the stone is at the bottom
of the circle?
Bottom of Circle
F c = FT - Fg
F T = Fc + Fg
= 50 + 9.8
= 59.8 N
5.10 An airplane pulls out of a dive in a circular arc whose radius is
1200 m. The airplane's velocity is a constant 200 m/s. Find the
force with which the 80-kg pilot presses down on his seat at the
bottom of the arc.
r = 1200 m
v = 200 m/s
m = 80 kg
Fc = FN - Fg
FN = Fc + Fg
mv 2
(80)( 200) 2
 (80)(9.8) = 3451 N
FN 
 mg 
1200
r
5.11 A ball at the end of an 80 cm string is being whirled in a
vertical circle. At what critical velocity vo will the string begin to go
slack at the top of the ball's path?
r = 0.8 m
Fc = FT + Fg
FT = 0
Fc = Fg
mv 2
 mg
r
v  rg  (0.8)(9.8) = 2.8 m/s
KEPLER’S FIRST LAW
"Every planet moves in an elliptical orbit with the Sun at
one focus."
KEPLER’S SECOND LAW
"As a planet moves in its orbit, a line drawn from the
Sun to the planet sweeps out equal areas in equal time
intervals."
As the planet is closest the sun, the
planet is moving fastest and as the
planet is farthest from the sun,it is
moving slowest. Nonetheless, the
imaginary line adjoining the center of
the planet to the center of the sun
sweeps out the same amount of area
in each equal interval of time.
KEPLER’S THIRD LAW
"If T is the period and r is the length of the semi-major
axis of a planet’s orbit, then the ratio T2/r3 is the same for
all planets."
T12 r13
 3
2
T2 r2
5.12 The mean distance from the Earth to the Sun is 1.496x108 km
and the period of its motion about the Sun is one year. The period
of Jupiter’s motion around the Sun is 11.86 years. Determine the
mean distance from the Sun to Jupiter.
TE2 rE3
 3
2
TJ
rJ
rE = 1.496x108
km
TE = 1 year
TJ = 11.86 years
T r
rJ  
 T
2 3
J E
2
E
1/ 3
  (11.86) 2 (1.496 x10 8 ) 3 1 / 3
8 km
  
=
7.77x10



(1) 2
 

NEWTON’S LAW OF UNIVERSAL GRAVITATION
Newton eventually proved that Kepler’s first two laws
imply a law of gravitation: Any two objects in the
Universe exert an attractive force on each other -called
the gravitational force- whose strength is proportional to
the product of the objects’ masses and inversely
proportional to the square of the distance between them.
If we let G be the universal gravitational constant, then
the strength of the gravitational force is given by the
equation:
m1m2
Units: Newtons (N)
F G 2
r
Cavendish determined the first reasonably accurate
numerical value for G more than one hundred years after
Newton’s Law was published. To three decimal places,
the currently accepted value is: G = 6.67 x10-11 N.m2/kg2
5.13 Derive Kepler’s Third Law from Newton’s Law of Gravitation.
For a Planet 1 of mass m1 and the Sun of mass MS
ΣF = ma = mac
Gm1 M S m1v12

2
r1
r1
2r1
v1 
T1
substituting:
GM S 4 2 r1

2
r1
T12
2
T12
4

rearranging:

3
GM S
r1
For a Planet 2 of mass m2 and the Sun of mass
MS:
therefore:
 T1

 T2
2

r 
   1 

 r2 
3
T22
4 2

3
GM S
r2
5.14 A 50 kg person and a 75 kg person are sitting on a bench so
that their centers are about 50 cm apart. Find the gravitational
force that each exerts on the other.
m1 = 50 kg
m2 = 75 kg
r = 0.5 m
Gm1 m2 6.67 x10 11 (50)(75)
F

2
r
(0.5) 2
= 1x10-6 N
5.15 What is the force of gravity acting on a 2000 kg spacecraft
when it orbits two Earth radii from the Earth’s center above the
Earth’s surface?
m1 = 2000 kg
ME = 5.98x1024 kg
rE = 6380x103 (2) =1.276x107
m
Gm1 m2 6.67 x10 11 (2000)(5.98x10 24 )

= 4899 N
F
7 2
2
(1.276 x10 )
r
5.16 Find the net force on the Moon due to the gravitational
attraction of both the Earth and the Sun assuming they are at right
angles to each other.
mM = 7.35x1022 kg
FEM
mS = 1.99 x1030 kg
Gm1 m2
mE = 5.98x1024 kg
F
2
r
8
rE = 3.84x10 kg
rS = 1.5x1011 m
FSM
FEM
6.67 x10 11 (7.35 x10 22 )(5.98 x10 24 )

= 1.99x1020 N
8 2
(3.84 x10 )
FSM
6.67 x10 11 (7.35 x10 22 )(1.99 x10 30 )
20 N

=
4.34
x10
(1.5 x1011 ) 2
FR  (1.99 x10 20 ) 2  (4.34 x10 20 ) = 4.77 x1020 N
5.17 a. Derive the expression for g from the Law of Universal
Gravitation.
Fg = FUG
GmM E
mg 
rE2
GM E
g 2
rE
b. Estimate the value of g on top of the Everest (8848 m) above the
Earth’s surface.
mE = 5.98x1024 kg
RE = 6.38x106 m
RT = 8848 + 6.38x106 = 6.388x106 m
GM E 6.67 x10 11 (5.98 x10 24 )
g 2 
2
=
9.77
m/s
6
2
rE
(6.388x10 )
SATELLITES
A satellite is put into orbit by accelerating it to a
sufficiently high tangential speed with the use of a
rocket. Satellites are usually put into circular (or nearly
circular) orbits because they require the least takeoff
speed. At the very high speed a satellite has, it would
quickly fly out into space if it weren’t for the
gravitational force of the Earth pulling it into orbit.
In fact, a satellite is falling
(accelerating toward the
Earth), but its high
tangential speed keeps it
from hitting Earth. The
force that gives a satellite
its acceleration is the force
of gravity.
Artificial satellites are launched at
different speeds in order to obtain
different orbits:
27,000 km/h for a circular orbit;
30,000 km/h for an elliptical orbit and
40,000 km/h for an escape velocity.
5.18 A geosynchronous satellite is one that stays above the same
point on the equator of the Earth. Determine:
a. The height above the Earth’s surface such a satellite must orbit
andm = 5.98x1024 kg
E
FUG = FC
R = 6.38x106 m
E
T = 1 day = 86400 s
GM E 4 2 r 2 4 2 r

 2
2
2
r
rT
T
GmS M E mS v 2

2
r
rE
GMET2 = 4 π2r3
GM E T 2 6.67 x10 11 (5.98 x10 24 )(86400) 2
r 

2
4
4 2
3
r = 4.23x107 m from the Earth’s
center
2r
v
T
height = r - rE
= 4.23x107 - 6.38x106 m
= 3.592x107 m
b. The satellite’s speed
GmS M E mS v 2

2
r
rE
GM E
v

r
6.67 x10 11 (5.98 x10 24 )
= 3070 m/s
7
4.23x10
APPARENT WEIGHT
The actual weight of a body is the gravitational force that
acts on it. The body's apparent weight is the force the
body exerts on whatever it rests on. Apparent weight
can be thought of as the reading on a scale a body is
placed on.
The figure shows a woman whose actual weight is 700 N
who is standing on a scale in an elevator. Her apparent
weight is equal to the force net.
FS
Fg
ΣF = FS - Fg = 0
FS = Fg
FS
a (+)
Fg
ΣF = FS - Fg = ma
FS = ma + Fg
FS
a (+)
Fg
ΣF = Fg - FS = ma
FS = Fg - ma
FS
a (+)
Fg
ΣF = Fg - FS = ma
for free fall a = g
so ma =mg = Fg
F S = Fg - Fg = 0
5.19 What will a spring scale read for the weight of a 75 kg man in
an elevator that moves:
m = 75 kg
Fg = 75(9.8) = 735 N
a. With constant upward speed of 5
m/s
ΣF = FS - Fg = 0
FS = Fg
= 735N
b. With constant downward speed of 5 m/s
FS = 735 N
c. With upward acceleration of 0.25 g
g = 0.25(9.8) = 2.45 m/s2
ΣF = FS - Fg = ma
FS = ma + Fg
= 75 (2.45) + 735
= 919 N
d. With downward acceleration of
0.25 g
ΣF = Fg - FS = ma
FS = Fg - ma
= 735 - 75 (2.45)
= 551 N
e. In free fall?
FS = 0 N