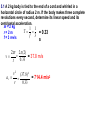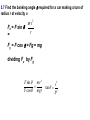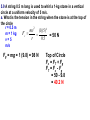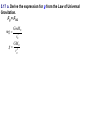* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PowerPoint Presentation - Mr. Cervantes Science Classes
Hunting oscillation wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Classical mechanics wikipedia , lookup
Jerk (physics) wikipedia , lookup
Equations of motion wikipedia , lookup
Coriolis force wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Fictitious force wikipedia , lookup
Mass versus weight wikipedia , lookup
Seismometer wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Centrifugal force wikipedia , lookup
Newton's laws of motion wikipedia , lookup
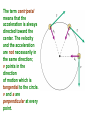
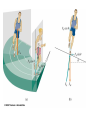
UNIFORM CIRCULAR MOTION Uniform circular motion is motion in which there is no change in speed, only a change in direction. CENTRIPETAL ACCELERATION An object experiencing uniform circular motion is continually accelerating. The position and velocity of a particle moving in a circular path of radius r are shown at two instants in the figure. When the particle is at point A, its velocity is represented by vector v1. After a time interval t, its velocity is represented by the vector v2. The acceleration is given by:v s chord v R v v2 v1 a t t radius as Δt becomes smaller and smaller, the chord length becomes equal to the arc length s = v Δt v v t v R v v 2 t R The term centripetal means that the acceleration is always directed toward the center. The velocity and the acceleration are not necessarily in the same direction; v points in the direction of motion which is tangential to the circle. v and a are perpendicular at every point. The period T is the time for one complete revolution. So the linear speed can be found by dividing the period into the circumference: 2r v T Units: m/s Another useful parameter in engineering problems is the rotational speed, expressed in revolutions per minute (rpm) or revolutions per second (rev/s). This quantity is called the frequency f of rotation and is given by the reciprocal of the period. 1 f T Units: s1 5.1 A 2 kg body is tied to the end of a cord and whirled in a horizontal circle of radius 2 m. If the body makes three complete revolutions every second, determine its linear speed and its centripetal m = 2 kg acceleration. r=2m f = 3 rev/s 1 1 T = 0.33 f 3 s 2r 2 ( 2) v = 37.8 m/s 0.33 t v 2 (37.8) 2 ac = 714.4 m/s2 r 0.33 5.2 A ball is whirled at the end of a string in a horizontal circle 60 cm in radius at the rate of 1 revolution every 2 s. Find the ball's centripetal acceleration. r = 0.6 m f = 1 rev/2 s t=2s v 2 (2r / t ) 2 ac r r 4 2 r 4 2 (0.6) 2 = 5.92 m/s 2 22 t CENTRIPETAL FORCE The inward force necessary to maintain uniform circular motion is defined as centripetal force. From Newton's Second Law, the centripetal force is given by: 2 mv Fc r 5.3 Two 4 N weights rotate about a center axis 3 m long at 12 rev/s,. a. What is the resultant force acting on each weight? Fg = 4 N f = 12 rev/ s v = 2πrf =2π (1.5)(12) = 113 m/s mv 2 (4 / 9.8)(113) 2 Fc = 3474 N 1.5 r b. What is the tension in the rod? The resultant force on each mass is equal to 3474 N directed toward the center. It is exerted by the center rod on the mass. The outward force we often think acts on the mass is actually the reaction force exerted by the mass on the rod. The tension in the rod is due to this outward force, and it is equal in magnitude to the centripetal force of 3474 N. The Forbidden F-Word When the subject of circular motion is discussed, it is not uncommon to hear mention of the word "centrifugal." Centrifugal, not to be confused with centripetal, means away from the center or outward. The use of or at least the familiarity with this word centrifugal, combined with the common sensation of an outward force when experiencing circular motion, often creates or reinforces a deadly student misconception. The deadly misconception, is the notion that objects in circular motion are experiencing an outward force. "After all," a well-meaning student may think, "I can recall vividly the sensation of being thrown outward away from the center of the circle on that roller coaster ride. Therefore, circular motion must be characterized by an outward force." Centrifugal Force is often used to describe why mud gets spun off a spinning tire, or water gets pushed out of the clothes during the spin dry cycle of your washer. It is also used to describe why we tend to slide to the outer side of a car going around a curve. Let’s imagine that you are riding in a car going around a curve. Sitting on your dashboard is a cassette tape. As you go around the curve, the tape moves to outside edge of the car. Because you don't want to blame it on ghosts, you say "centrifugal force pushed the tape across the dashboard.“ Wwrroonngg!! When we view this situation from above the car, we get a better view of what is really happening. The animation shows both views at the same time. The top window shows you the passenger's view of the car and the tape, while the bottom window shows you the bird's eye view. There is enough static friction on the sides of the tires to act as centripetal force which forces the car to stay in the circular path. The tape on the slippery dashboard does not have enough friction to act as a centripetal force, so in the absence of a centripetal force the tape follows straight line motion. The car literally turns out from underneath the tape, but from the passenger's point of view it looks as though something (a ghost force?) pushed the tape across the dashboard. If the car you are riding in has the windows rolled down, then the tape will leave the car (or does the car leave the tape?) as it follows its straight line path. If the windows are rolled up, then the window will deliver a centripetal force to the tape and keep it in a circular path. Without a centripetal force, an object in motion continues along a straight-line path. With a centripetal force, an object in motion will be accelerated and change its direction. 5.4 A 1000-kg car rounds a turn of radius 30 m at a velocity of 9 m/s a. How much centripetal force is required? m = 1000 kg r = 30 m v = 9 m/s mv 2 (1000)(9) 2 Fc = 2700 30 r N b. Where does this force come from? Force of friction between tires and road. When an automobile is driven around a sharp turn on a perfectly level road, friction between the tires and the road provides the centripetal force. If this force is not adequate, the car may slide off the road. The maximum value of the force of friction determines the maximum speed with which a car can negotiate a turn of a given radius. 5.5 The maximum force a road can exert on the tires of a 1500-kg car is 8500 N. What is the maximum velocity at which the car can round a turn of radius 120 m? m = 1500 kg F = 8500 N r = 120 m v mv 2 Fc r Fr 8500(120) = 26 m/s (94 km/h) 1500 m 5.6 A car is traveling at 20 km/h on a level road where the coefficient of static friction between tires and road is 0.8. Find the minimum turning radius of the car. v = 5.55 m/s μ = 0.8 Fc = Ff mv 2 s mg r (5.55) 2 v2 r = 3.93 m s g 0.8(9.8) If we consider the effects of banking a turn to eliminate the friction force we observe that the horizontal component of the normal force provides the necessary centripetal force. 5.7 Find the banking angle required for a car making a turn of radius r at velocity v. mv 2 Fx = F sin r = Fy = F cos = Fg = mg dividing Fx by Fg F sin mv 2 F cos mgr v2 tan gr The proper banking angle depends only on v and r, not on the mass of the car. If a car goes around a banked turn more slowly than at the design velocity, friction tends to keep it from sliding down the inclined roadway; if the car goes faster, friction tends to keep it from skidding outward. If the car's speed is too great, however, friction may not be sufficient to keep the car on the road. 5.8 a. Find the required banking angle for a curve of radius 300 m if the curve is to be negotiated at a speed of 80 km/h. r = 300 m v = 22.2 m/s v2 tan gr (22.2) 2 = 9.5˚ tan 9.8(300) 1 b. If the curve were not banked, what coefficient of friction would be required between the tires and the road? From problem 5.6 v2 r s g v 2 (22.2) 2 s = 0.17 rg 9.8(300) MOTION IN A VERTICAL CIRCLE When a body moves in a vertical circle at the end of a string, the tension FT in the string varies with the body's position. The centripetal force Fc on the body at any point is the vector sum of FT and the component of the body's weight toward the center of the circle. The figure shows the forces exerted on an airplane at the upper and lower limits of a vertical loop. At the highest point in the circular turn the centripetal force is given by:2 mv F1 mg R When the aircraft passes through the lowest point in the loop the 2 mv centripetal F2 mg R force is: 5.9 A string 0.5 m long is used to whirl a 1-kg stone in a vertical circle at a uniform velocity of 5 m/s. a. What is the tension in the string when the stone is at the top of the circle r = 0.5 m mv 2 (1)(5) 2 m = 1 kg Fc = 50 N 0. 5 r v=5 m/s Fg = mg = 1 (9.8) = 98 N Top of Circle Fc = FT + Fg FT = Fc - Fg = 50 - 9.8 = 40.2 N b. What is the tension in the string when the stone is at the bottom of the circle? Bottom of Circle F c = FT - Fg F T = Fc + Fg = 50 + 9.8 = 59.8 N 5.10 An airplane pulls out of a dive in a circular arc whose radius is 1200 m. The airplane's velocity is a constant 200 m/s. Find the force with which the 80-kg pilot presses down on his seat at the bottom of the arc. r = 1200 m v = 200 m/s m = 80 kg Fc = FN - Fg FN = Fc + Fg mv 2 (80)( 200) 2 (80)(9.8) = 3451 N FN mg 1200 r 5.11 A ball at the end of an 80 cm string is being whirled in a vertical circle. At what critical velocity vo will the string begin to go slack at the top of the ball's path? r = 0.8 m Fc = FT + Fg FT = 0 Fc = Fg mv 2 mg r v rg (0.8)(9.8) = 2.8 m/s KEPLER’S FIRST LAW "Every planet moves in an elliptical orbit with the Sun at one focus." KEPLER’S SECOND LAW "As a planet moves in its orbit, a line drawn from the Sun to the planet sweeps out equal areas in equal time intervals." As the planet is closest the sun, the planet is moving fastest and as the planet is farthest from the sun,it is moving slowest. Nonetheless, the imaginary line adjoining the center of the planet to the center of the sun sweeps out the same amount of area in each equal interval of time. KEPLER’S THIRD LAW "If T is the period and r is the length of the semi-major axis of a planet’s orbit, then the ratio T2/r3 is the same for all planets." T12 r13 3 2 T2 r2 5.12 The mean distance from the Earth to the Sun is 1.496x108 km and the period of its motion about the Sun is one year. The period of Jupiter’s motion around the Sun is 11.86 years. Determine the mean distance from the Sun to Jupiter. TE2 rE3 3 2 TJ rJ rE = 1.496x108 km TE = 1 year TJ = 11.86 years T r rJ T 2 3 J E 2 E 1/ 3 (11.86) 2 (1.496 x10 8 ) 3 1 / 3 8 km = 7.77x10 (1) 2 NEWTON’S LAW OF UNIVERSAL GRAVITATION Newton eventually proved that Kepler’s first two laws imply a law of gravitation: Any two objects in the Universe exert an attractive force on each other -called the gravitational force- whose strength is proportional to the product of the objects’ masses and inversely proportional to the square of the distance between them. If we let G be the universal gravitational constant, then the strength of the gravitational force is given by the equation: m1m2 Units: Newtons (N) F G 2 r Cavendish determined the first reasonably accurate numerical value for G more than one hundred years after Newton’s Law was published. To three decimal places, the currently accepted value is: G = 6.67 x10-11 N.m2/kg2 5.13 Derive Kepler’s Third Law from Newton’s Law of Gravitation. For a Planet 1 of mass m1 and the Sun of mass MS ΣF = ma = mac Gm1 M S m1v12 2 r1 r1 2r1 v1 T1 substituting: GM S 4 2 r1 2 r1 T12 2 T12 4 rearranging: 3 GM S r1 For a Planet 2 of mass m2 and the Sun of mass MS: therefore: T1 T2 2 r 1 r2 3 T22 4 2 3 GM S r2 5.14 A 50 kg person and a 75 kg person are sitting on a bench so that their centers are about 50 cm apart. Find the gravitational force that each exerts on the other. m1 = 50 kg m2 = 75 kg r = 0.5 m Gm1 m2 6.67 x10 11 (50)(75) F 2 r (0.5) 2 = 1x10-6 N 5.15 What is the force of gravity acting on a 2000 kg spacecraft when it orbits two Earth radii from the Earth’s center above the Earth’s surface? m1 = 2000 kg ME = 5.98x1024 kg rE = 6380x103 (2) =1.276x107 m Gm1 m2 6.67 x10 11 (2000)(5.98x10 24 ) = 4899 N F 7 2 2 (1.276 x10 ) r 5.16 Find the net force on the Moon due to the gravitational attraction of both the Earth and the Sun assuming they are at right angles to each other. mM = 7.35x1022 kg FEM mS = 1.99 x1030 kg Gm1 m2 mE = 5.98x1024 kg F 2 r 8 rE = 3.84x10 kg rS = 1.5x1011 m FSM FEM 6.67 x10 11 (7.35 x10 22 )(5.98 x10 24 ) = 1.99x1020 N 8 2 (3.84 x10 ) FSM 6.67 x10 11 (7.35 x10 22 )(1.99 x10 30 ) 20 N = 4.34 x10 (1.5 x1011 ) 2 FR (1.99 x10 20 ) 2 (4.34 x10 20 ) = 4.77 x1020 N 5.17 a. Derive the expression for g from the Law of Universal Gravitation. Fg = FUG GmM E mg rE2 GM E g 2 rE b. Estimate the value of g on top of the Everest (8848 m) above the Earth’s surface. mE = 5.98x1024 kg RE = 6.38x106 m RT = 8848 + 6.38x106 = 6.388x106 m GM E 6.67 x10 11 (5.98 x10 24 ) g 2 2 = 9.77 m/s 6 2 rE (6.388x10 ) SATELLITES A satellite is put into orbit by accelerating it to a sufficiently high tangential speed with the use of a rocket. Satellites are usually put into circular (or nearly circular) orbits because they require the least takeoff speed. At the very high speed a satellite has, it would quickly fly out into space if it weren’t for the gravitational force of the Earth pulling it into orbit. In fact, a satellite is falling (accelerating toward the Earth), but its high tangential speed keeps it from hitting Earth. The force that gives a satellite its acceleration is the force of gravity. Artificial satellites are launched at different speeds in order to obtain different orbits: 27,000 km/h for a circular orbit; 30,000 km/h for an elliptical orbit and 40,000 km/h for an escape velocity. 5.18 A geosynchronous satellite is one that stays above the same point on the equator of the Earth. Determine: a. The height above the Earth’s surface such a satellite must orbit andm = 5.98x1024 kg E FUG = FC R = 6.38x106 m E T = 1 day = 86400 s GM E 4 2 r 2 4 2 r 2 2 2 r rT T GmS M E mS v 2 2 r rE GMET2 = 4 π2r3 GM E T 2 6.67 x10 11 (5.98 x10 24 )(86400) 2 r 2 4 4 2 3 r = 4.23x107 m from the Earth’s center 2r v T height = r - rE = 4.23x107 - 6.38x106 m = 3.592x107 m b. The satellite’s speed GmS M E mS v 2 2 r rE GM E v r 6.67 x10 11 (5.98 x10 24 ) = 3070 m/s 7 4.23x10 APPARENT WEIGHT The actual weight of a body is the gravitational force that acts on it. The body's apparent weight is the force the body exerts on whatever it rests on. Apparent weight can be thought of as the reading on a scale a body is placed on. The figure shows a woman whose actual weight is 700 N who is standing on a scale in an elevator. Her apparent weight is equal to the force net. FS Fg ΣF = FS - Fg = 0 FS = Fg FS a (+) Fg ΣF = FS - Fg = ma FS = ma + Fg FS a (+) Fg ΣF = Fg - FS = ma FS = Fg - ma FS a (+) Fg ΣF = Fg - FS = ma for free fall a = g so ma =mg = Fg F S = Fg - Fg = 0 5.19 What will a spring scale read for the weight of a 75 kg man in an elevator that moves: m = 75 kg Fg = 75(9.8) = 735 N a. With constant upward speed of 5 m/s ΣF = FS - Fg = 0 FS = Fg = 735N b. With constant downward speed of 5 m/s FS = 735 N c. With upward acceleration of 0.25 g g = 0.25(9.8) = 2.45 m/s2 ΣF = FS - Fg = ma FS = ma + Fg = 75 (2.45) + 735 = 919 N d. With downward acceleration of 0.25 g ΣF = Fg - FS = ma FS = Fg - ma = 735 - 75 (2.45) = 551 N e. In free fall? FS = 0 N