* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Differential Amplifiers
Transistor–transistor logic wikipedia , lookup
Regenerative circuit wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Schmitt trigger wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Valve audio amplifier technical specification wikipedia , lookup
Opto-isolator wikipedia , lookup
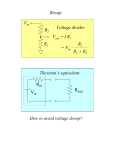
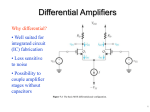
類比電路設計(3349) - 2004 Differential Amplifiers Ching-Yuan Yang National Chung-Hsing University Department of Electrical Engineering Overview z Reading B. Razavi Chapter 4. z Introduction Offering many useful properties, differential operation has become the dominant choice in today’s high-performance analog and mixed-signal circuits. This lecture deals with the analysis and design of CMOS differential amplifiers. It contains: Review of single-ended and differential operation. Analysis of the large-signal and small-signal behavior. The common-mode rejection. Differential pair with diode-connected and current-source loads as well as differential cascode stages. Analog-Circuit Design 4-1 Ching-Yuan Yang / EE, NCHU 1 Single-ended and differential operation z Single-ended and differential signals z What are “common-mode” (CM) and “differential mode” (DM)? Analog-Circuit Design 4-2 Ching-Yuan Yang / EE, NCHU Advantages of differential operation z Reduction of coupling z Common-mode rejection occurs with noisy supply voltages Analog-Circuit Design 4-3 Ching-Yuan Yang / EE, NCHU 2 Advantages of differential operation (cont’d) z Reduction of coupled noise by differential operation z Increase in maximum achievable voltage swing z Simpler biasing z Higher linearity Analog-Circuit Design 4-4 Ching-Yuan Yang / EE, NCHU 4-5 Ching-Yuan Yang / EE, NCHU Simple differential circuit Analog-Circuit Design 3 Basic differential pair z Schematic –- source-coupled pair The differential pair employs a current source ISS to make ID1 + ID2 indepent of Vin,CM. Thus, if Vin1 = Vin2, the bias current of each transistor equqls ISS /2 and the output common-mode level is VDD − RDISS /2. Analog-Circuit Design 4-6 Ching-Yuan Yang / EE, NCHU Basic differential pair (cont’d) z Qualitative analysis Input/output characteristics Analog-Circuit Design 4-7 Ching-Yuan Yang / EE, NCHU 4 Common-mode characteristics z Common-mode schematic z Common-mode input/output characteristics Analog-Circuit Design Ching-Yuan Yang / EE, NCHU 4-8 Common-mode characteristics z Input common-mode range – M1, M2 in saturation I VGS1 + (VGS 3 − VTH 3 ) ≤ Vin ,CM ≤ minVDD − RD SS + VTH , 2 VDD z The small-signal differential gain of a differential pair vs. the input CM level M1, M2 sat. Analog-Circuit Design 4-9 M1, M2 triode Ching-Yuan Yang / EE, NCHU 5 Output swing of a differential pair z For M1 and M2 to be saturated, each output can go as high as VDD but as low as approximately Vin,CM − VTH. In other words, the higher the input CM level, the smaller the allowable output swings. For this reason, it is desirable to choose a relatively low Vin,CM. z An trade-off exists between the maximum value of Vin,CM and differential gain. Similar to a simple CS stage, the gain of a differential pair is a function is a function of the dc drop across the load resistors. Thus, if RDISS /2 is large, Vin,CM must remain close to ground potential. Analog-Circuit Design 4-10 Ching-Yuan Yang / EE, NCHU Quantitative analysis z Differential pair Ö Vout1 = VDD − RD1ID1 , Vout2 = VDD − RD2ID2 [RD1 = RD2 = RD] Vout1 − Vout2 = RD2ID2 − RD1ID1 = RD (ID2 − ID1) Assuming the circuit is symmetric, M1 and M2 are saturated, and λ = 0, Vin1 − Vin2 = VGS1 − VGS2 For a square-law device, we have: Therefore, Vin1 − Vin 2 = 2I D 2 2I D1 − W W µnCox µnCox L L Recognizing that ID2 + ID1 = ISS, we obtain Analog-Circuit Design 4-11 Ching-Yuan Yang / EE, NCHU 6 Quantitative analysis (cont’d) (Vin1 − Vin 2 )2 = Ö 2 µnCox W L (I SS − 2 I D1I D 2 ) 1 W µnCox (Vin1 − Vin 2 )2 − I SS = −2 I D1I D 2 2 L Squaring the two sides again and 4ID1ID2 = (ID1 + ID2)2 − (ID1 − ID2)2 = ISS2 − (ID1 − ID2)2 , we arrive at I D1 − I D 2 = W 1 4I SS 2 − (Vin1 − Vin 2 ) µnCox (Vin1 − Vin 2 ) W L 2 µnCox L Denoting ∆ID = ID1 − ID2 and ∆Vin = Vin1 − Vin2 , we can show that 4I SS − 2∆Vin2 1 ∂∆I D W µnCoxW / L = µnCox 4I SS ∂∆Vin 2 L − ∆Vin2 µnCoxW / L Analog-Circuit Design 4-12 Ching-Yuan Yang / EE, NCHU Quantitative analysis (cont’d) For ∆Vin = 0, Gm = ∂∆I D ∂∆Vin V = in µnCox =0 W I SS L Since ∆Vout = Vout1 − Vout2 = RD ∆ID = RDGM∆Vin, the small-signal differential gain is given as Av = Gm RD = GM = 0 for ∆Vin = z µnCox W I SS ⋅ RD L 2I SS µnCoxW / L Variation of ID and GM vs. ∆Vin ISS Analog-Circuit Design 4-13 Ching-Yuan Yang / EE, NCHU 7 Quantitative analysis (cont’d) ISS z For a zero differential input, ID1 = ID2 = ISS /2, and hence (VGS − VTH )1,2 = I SS µnCox W L = ∆Vin 2 Increasing ∆Vin to make the circuit more linear inevitably increases the overdrive voltage of M1 and M2. For a given ISS, this is only by reducing W/L and hence the gm of the transistors. Analog-Circuit Design Ching-Yuan Yang / EE, NCHU 4-14 Quantitative analysis (cont’d) z Input/output characteristic z As W/L increases, ∆Vin decreases, narrowing the input range across which both devices are on. Analog-Circuit Design 4-15 z As ISS increases, both the input range and the output current swing increase. Ching-Yuan Yang / EE, NCHU 8 Differential pair with small-signal inputs z Scheme – M1 and M2 sat., small signals Vin1 and Vin2. z Analysis Ö Differential pair sensing one input signal. Analog-Circuit Design Circuit viewed as a CS stage degenerated by M2. 4-16 RS = 1/ gm 2 VX RD =− 1 1 Vin1 + g m1 g m 2 Equivalent circuit. Ching-Yuan Yang / EE, NCHU Differential pair with small-signal inputs (cont’d) z Replacing M1 by a Thevenin equivalent VT = Vin1 RT = 1/gm1 M2 operates as a CG stage, exhibiting a gain equal to VY RD = 1 1 Vin1 + g m 2 g m1 2R D V 1 1 in1 + g m1 g m 2 = gm reduces to is (VX − VY)|Due to Vin1 = − gmRDVin1. The overall voltage for Vin1 is (VX − VY)|Due to Vin1 = − which, for gm1 = gm2 Similarly, (VX − VY)|Due to Vin2 = − gmRDVin2. Thus, we have Analog-Circuit Design 4-17 (VX − VY )tot = − gm R D Vin1 − Vin 2 Ching-Yuan Yang / EE, NCHU 9 Differential and common-mode components Vin1 − Vin 2 Vin1 + Vin 2 + 2 2 Vin 2 − Vin1 Vin1 + Vin 2 = + 2 2 Vin1 = Vin 2 Analog-Circuit Design 4-18 Ching-Yuan Yang / EE, NCHU Differential and common-mode components (cont’d) z Superposition for differential and common-mode signals Vin1 − Vin 2 Vin1 + Vin 2 + 2 2 Vin 2 − Vin1 Vin1 + Vin 2 = + 2 2 Vin1 = Vin 2 Analog-Circuit Design 4-19 Ching-Yuan Yang / EE, NCHU 10 Differential and common-mode components (cont’d) z λ≠0 Common-mode operation Differential-mode operation V − Vin 2 V X = −gm (RD ro1 ) in1 2 Vin 2 − Vin1 VY = −gm (RD ro 2 ) 2 V X − VY = −gm (RD ro ) Vin1 − Vin 2 Analog-Circuit Design If the circuit is fully symmetric and ISS an ideal current source, the current drawn by M1 and M2 from RD1 and RD2 is exactly equal to ISS /2 and independent of Vin,CM . Thus, VX and VY experience no change as Vin,CM varies. Ching-Yuan Yang / EE, NCHU 4-20 Common-mode response z Differential pair sensing CM input Av ,CM = RSS : the output impedance of current source. Analog-Circuit Design 4-21 Vout RD /2 =− 1 Vin ,CM + RSS 2gm (λ=γ=0) Ching-Yuan Yang / EE, NCHU 11 Common-mode response with mismatch z Resistor mismatch ∆V X = − ∆Vin ,CM gm RD 1 + 2gm RSS ∆VY = − ∆Vin ,CM gm (RD + ∆RD ) 1 + 2gm RSS A CM change at the input introduces a differential component at the output. • CM response with finite tail cap. • Effect of CM noise Analog-Circuit Design 4-22 Ching-Yuan Yang / EE, NCHU Common-mode response with mismatch (cont’d) z Mismatch between M1 and M2 I D1 = gm1 (Vin ,CM − VP ) I D 2 = gm 2 (Vin ,CM − VP ) ⇒ (gm1 + gm 2 ) (Vin ,CM − VP ) = VP / RSS ⇒ VP = (gm1 + gm 2 )RSS V (gm1 + gm 2 )RSS + 1 in ,CM gm1 VX = −gm1(Vin,CM −VP )RD = − (g + g )R +1RDVin,CM gm1 − gm2 m1 m2 SS RDVin,CM ⇒ VX −VY = − gm2 g ( + gm2 )RSS +1 m 1 VY = −gm2(Vin,CM −VP )RD = − RDVin,CM (gm1 + gm2 )RSS +1 ∆gm RD ACM −DM = − (gm1 + gm 2 )RSS + 1 Thus, the circuit converts input CM variations to a differential error by a factor equal to Analog-Circuit Design ACM−DM : CM to DM conversion ∆gm = gm1 − gm2 4-23 Ching-Yuan Yang / EE, NCHU 12 Common-mode rejection ratio (CMRR) z Definition CMRR = ADM ACM −DM z If only gm mismatch is considered Differential mode (assume Vin1 = −Vin2) ADM = RD gm1 + gm 2 + 4gm1gm 2RSS 2 1 + (gm1 + gm 2 )RSS Common-mode to differential-mode conversion ACM −DM = − ∆gm RD (gm1 + gm 2 )RSS RS = (1/ gm 2 ) RSS +1 CMRR CMRR = ≈ gm1 + gm 2 + 4gm1gm 2RSS 2∆gm gm [1 + 2gm RSS ] ∆gm Analog-Circuit Design 4-24 Ching-Yuan Yang / EE, NCHU Differential pair with MOS loads z Diode-connected load z Current-source load −1 Av = −gmN (gmP roN roP ) Av = −gmN (roN roP ) g ≈ − mN gmP =− µn (W / L )N µ p (W / L )P Analog-Circuit Design 4-25 Ching-Yuan Yang / EE, NCHU 13 Differential pair with MOS loads (cont’d) z Diode-connected + current source loads z Cascode differential pair Av ≈ gm1[(gm 3ro 3ro1 ) (gm 5ro 5ro 7 )] Half circuit Analog-Circuit Design 4-26 Ching-Yuan Yang / EE, NCHU Variable-gain amplifier (VGA) z Simple VGA Av = Vout /Vin varies from zero (if ID3 = 0) to a maximum value given by voltage headroom limitations and device dimensions. VGAs find application in systems where the signal amplitude may experience large variations and hence requires inverse change in the gain. z Two stages providing variable gain Consider two differential pairs that amplify the input by opposite gain. We now have Vout1/Vin = −gmRD and , where gm denotes the transconductance of each transistor in equilibrium. If I1 and I2 vary in opposite directions, so do |Vout1/Vin| and |Vout2/Vin|. Analog-Circuit Design 4-27 Ching-Yuan Yang / EE, NCHU 14 Gilbert cell Vout = Vout1 + Vout2 = A1Vin + A2Vin If I1 = 0, then Vout = +gmRDVin. If I2 = 0, then Vout = −gmRDVin. For I1 = I2, the gain drops to zero. Vcont1 and Vcont2 vary I1 and I2 in opposite directions such that the gain of the amplifier changes monotonically. For Vcont1 = Vcont2, the gain is zero. For M5-6 to operate in saturation, the CM level of Vcont, VCM,cont, must be such that VCM,cont ≤ VCM,in − VGS1 + VTH5,6. Analog-Circuit Design 4-28 Ching-Yuan Yang / EE, NCHU Gilbert cell (cont’d) Gilbert cell sensing the input voltage by the bottom differential pair Analog-Circuit Design For very positive Vcont, For very negative Vcont, Vout = gm5,6RDVin. Vout = −gm5,6RDVin. 4-29 Ching-Yuan Yang / EE, NCHU 15