* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Astronomical Scale
Survey
Document related concepts
Heliosphere wikipedia , lookup
Late Heavy Bombardment wikipedia , lookup
History of Solar System formation and evolution hypotheses wikipedia , lookup
Near-Earth object wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
Space: 1889 wikipedia , lookup
Transcript
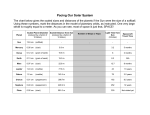
Astronomical Scale |1 Astronomical Scale Astronomy is the study of the universe, and when studying the universe, we often deal with unbelievable sizes and unfathomable distances. To help us get a better understanding of these sizes and distances, we can put them to scale. Scale is the ratio between the actual object and a model of that object. Some common examples of scaled objects are maps, toy model kits, and statues. Maps and toy model kits are usually much smaller than the object it represents, whereas statues are normally larger than its analog. Today, we will create a scaled model of our solar system. To do this, we must find a ratio. We start by selecting an object [1] we would like the solar system to be scaled to. For our convenience, we will use a yellow fitness ball as today’s representation for our sun. Next, look for a common parameter. Let’s use the diameters of the fitness ball and the Sun [2]. The diameter of our fitness ball is 24” (inches). The diameter of the Sun is 1,400,000𝑘𝑚 (kilometers). Before we go on, we must determine the system of units [3] that we want to use. Doing so greatly reduces the chance for miscalculations. In astronomy, like in all sciences, we use the metric system, also known as the International System of Units (SI for short). Department of Physics & Astronomy Astronomical Scale |2 The metric system is a base-10 system, which essentially means it is very easy to change and use units within this system. Our fitness ball is in the imperial system. To convert it, let’s use a unit in the metric system that is similar in size to inches. Here, we’ll change inches to centimeters (𝑐𝑚). One inch is exactly 2.54𝑐𝑚, and the diameter of our fitness ball is 24”, so multiply 2.54𝒄𝒎 by 24 [4]. We conclude that the diameter of the fitness ball is about 61𝑐𝑚. Now that the measurements are in the same system, we need to check if the units are the same between the fitness ball and the Sun. Our fitness ball is in centimeters and the Sun is in kilometers, so clearly, they are not the same. Let’s change that. The metric system is based off the meter (hence the name of the system), so let’s convert the centimeters and kilometers into meters. “centi-“ means one hundredth (0.01) and “kilo-“ means one thousand (1,000), so 1𝑐𝑚 is one hundredth of a meter and 1𝑘𝑚 is one thousand meters. We can now change units of the fitness ball and the Sun with this knowledge. For the fitness ball, multiply 61𝒄𝒎 by 0.01. For the Sun, multiply 1,400,000𝒌𝒎 by 1,000 [5]. We conclude that the diameter of the ball is 0.61𝑚 and the diameter of the Sun is 1,400,000,000𝑚. Department of Physics & Astronomy Astronomical Scale |3 We can finally determine our ratio! To do this, always divide the size of the object you want to scale to (the numerator) by the size of the actual object (the denominator). In our case, divide the diameter of the fitness ball by the diameter of the Sun [6]. We conclude that this number is about 0.0000000004.4. Note that the units canceled each other out. This can be written in scientific notation as 4.4 X 10-10 or 4.4E-10, both of which are clearer to read. We will use 4.4E-10 because it is easier to type this number style into our calculators. Now that we have figured out our model’s ratio, we can calculate the scaled sizes of the planets and their relative distances. As an example, we’ll take Mercury, the closest planet to the Sun. The diameter of Mercury is roughly 4,900𝑘𝑚. Note that this number’s units are in kilometers. Our ratio was determined by using meters, however, so we must change the diameter of the object into meters [7]. Mercury’s actual diameter in meters is 4,900,000𝑚. With this number, multiply the actual diameter of the object by our ratio [8]. We conclude that Mercury’s diameter in our model is about 0.0021𝑚 or 0.21𝑐𝑚, about the width of the tip of a crayon. Department of Physics & Astronomy Astronomical Scale |4 The distance that Mercury is from the Sun varies because Mercury revolves around the Sun in an elliptical pattern, but we will use the semi-major axis, the farthest distance the planet is from the Sun. This is nearly 58,000,000𝑘𝑚 for Mercury. As we did previously, we need to change kilometers into meters. So using 58,000,000,000𝑚 instead, multiply the semimajor axis by our ratio [9]. We conclude that the closest planet is surprisingly far away from our fitness ball – a distant 25 meters away! Now that I’ve shown you how to scale down our solar system to the fitness ball standard, determine with a partner the sizes and distances for the other seven planets. Once you are done, come up to the desk and select the object that best represents the size for each of your planets. At the end of the lab, we will go outside and try to visualize just how far our models are from each other. Department of Physics & Astronomy Astronomical Scale |5 Example Sheet Determine the Ratio 1. Select the fitness ball as the object that the Sun will be scaled to. 2. The diameter of the fitness ball is 24”, and the diameter of the Sun is 1,400,000𝑘𝑚. 3. Use the metric system. 4. 2.54𝑐𝑚 = 1”, so: 2.54𝑐𝑚 ∗ 24 ≈ 61𝑐𝑚 1 5. The fitness ball needs to be in meters, so: 61𝑐𝑚 1𝑚 ∗ = 0.61𝑚 1 100𝑐𝑚 And the Sun needs to be in meters as well, so: 1,400,000𝑘𝑚 1,000𝑚 ∗ = 1,400,000,000𝑚 1 1𝑘𝑚 6. To get the ratio, we divide the diameter of the fitness ball by the Sun: 0.61𝑚 1,400,000,000𝑚 ≈ 4.4E-10 Department of Physics & Astronomy Astronomical Scale |6 Determine the Scaled Diameter 7. Our object is Mercury, so: 4,900𝑘𝑚 1,000𝑚 ∗ = 4,900,000𝑚 1 1𝑘𝑚 8. Mercury’s actual diameter multiplied by our ratio is: 4,900,000𝑚 ∗ 4.4E-10 ≈ 0.0021𝑚 0.0021𝑚 100𝑐𝑚 ∗ = 0.21𝑐𝑚 1 1𝑚 Determine the Scaled Distance 9. The semi-major axis of Mercury is 58,000,000𝑘𝑚, so: 58,000,000𝑘𝑚 1,000𝑚 ∗ = 58,000,000,000𝑚 1 1𝑘𝑚 58,000,000,000𝑚 ∗ 4.4E-10 ≈ 26𝑚 Department of Physics & Astronomy Astronomical Scale |7 Work Sheet 1. Actual Diameter of Mercury Scaled Diameter of Mercury 4,900𝑘𝑚 1 ∗ 1,000𝑚 1𝑘𝑚 = 4,900,000𝑚 : 4,900,000𝑚 ∗ 4.4E-10 = 0.0021𝑚 0.0021𝑚 100𝑐𝑚 ∗ = 0.21𝑐𝑚 1 1𝑚 2. Actual Diameter of Venus Scaled Diameter of Venus 3. Actual Diameter of Earth Scaled Diameter of Earth 4. Actual Diameter of Mars Scaled Diameter of Mars 5. Actual Diameter of Jupiter Scaled Diameter of Jupiter 6. Actual Diameter of Saturn Scaled Diameter of Saturn 7. Actual Diameter of Uranus Scaled Diameter of Uranus 8. Actual Diameter of Neptune Scaled Diameter of Neptune Department of Physics & Astronomy Astronomical Scale |8 1. Actual Distance of Mercury Scaled Distance of Mercury 5,800,000𝑘𝑚 1 ∗ 1,000𝑚 1𝑘𝑚 = 5,800,000,000𝑚; 5,800,000,000𝑚 ∗ 4.4E-10 ≈ 26𝑚 2. Actual Distance of Venus Scaled Distance of Venus 3. Actual Distance of Earth Scaled Distance of Earth 4. Actual Distance of Mars Scaled Distance of Mars 5. Actual Distance of Jupiter Scaled Distance of Jupiter 6. Actual Distance of Saturn Scaled Distance of Saturn 7. Actual Distance of Uranus Scaled Distance of Uranus 8. Actual Distance of Neptune Scaled Distance of Neptune Department of Physics & Astronomy Astronomical Scale |9 Data Sheet Solar System Object Actual Diameter (𝑘𝑚) Actual Diameter (𝑚) Scaled Diameter (𝑐𝑚) Portrayal of Scaled Object Sun 1,400,000 1,400,000,000 61 Fitness Ball Mercury 4,900 4,900,000 0.21 Venus 12,000 Earth 13,000 Mars 6,800 Jupiter 140,000 Saturn 120,000 Uranus 51,000 Neptune 49,000 Department of Physics & Astronomy A s t r o n o m i c a l S c a l e | 10 Data Sheet Solar System Object Actual Distance (𝑘𝑚) Actual Distance (𝑚) Scaled Distance (𝑚) Sun 0 0 0 Mercury 58,000,000 58,000,000,000 26 Venus 110,000,000 Earth 150,000,000 Mars 230,000,000 Jupiter 780,000,000 Saturn 1,400,000,000 Uranus 2,900,000,000 Neptune 4,500,000,000 Department of Physics & Astronomy A s t r o n o m i c a l S c a l e | 11 Homework Scale the Sun to the Sunsphere, and use this new ratio to determine the semi-major axial distances of the eight planets. The diameter of the Sunsphere is 74’ (feet). Follow the Example Sheet if you need a reference. Remember that 1 foot equals 12 inches. Solar System Object Actual Distance (𝑘𝑚) Actual Distance (𝑚) Scaled Distance (𝑚) Sun 0 0 0 Mercury 58,000,000 Venus 110,000,000 Earth 150,000,000 Mars 230,000,000 Jupiter 780,000,000 Saturn 1,400,000,000 Uranus 2,900,000,000 Neptune 4,500,000,000 Department of Physics & Astronomy A s t r o n o m i c a l S c a l e | 12 Homework Work Sheet 1. Determine the Ratio 2. Actual Distance of Mercury Scaled Distance of Mercury 3. Actual Distance of Venus Scaled Distance of Venus 4. Actual Distance of Earth Scaled Distance of Earth 5. Actual Distance of Mars Scaled Distance of Mars 6. Actual Distance of Jupiter Scaled Distance of Jupiter 7. Actual Distance of Saturn Scaled Distance of Saturn 8. Actual Distance of Uranus Scaled Distance of Uranus 9. Actual Distance of Neptune Scaled Distance of Neptune Department of Physics & Astronomy