* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Orbits
Equation of time wikipedia , lookup
Earth's rotation wikipedia , lookup
Giant-impact hypothesis wikipedia , lookup
Late Heavy Bombardment wikipedia , lookup
Standard solar model wikipedia , lookup
Space: 1889 wikipedia , lookup
History of Solar System formation and evolution hypotheses wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
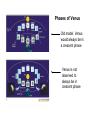
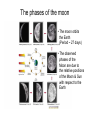
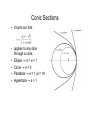
Orbits • Observable - Mercury & Venus are always in close proximity to the Sun, and either trail or lead the Sun in the sky • Observable - Mars, Jupiter, & Saturn are not restricted to close proximity to the Sun, & are seen to make loops in the sky during opposition with the Sun • Observable - The Sun & planets follow a narrow path through the sky through 12 constellations (Zodiac). Mars, Jupiter, & Saturn move at a slower pace through the Zodiac than the Sun, Mercury, & Venus. • Observable - The Moon is seen to go through phases on an ~ 29-day cycle. Old belief - Geocentric (EarthCentered) Model • Ptolemaic System (after Ptolemy, 2nd century A.D.) Geocentric • • • • Observable - Mercury & Venus are always in close proximity to the Sun, and either trail or lead the Sun in the sky. Me & V orbit the Earth, but go through epicycles. Their orbits have the same period as the Sun’s period around the Earth Observable - Mars, Jupiter, & Saturn are not restricted to close proximity to the Sun, & are seen to make loops in the sky during opposition with the Sun. Ma, J, & Sa’s have different orbital period around the Earth than Me, V, and the Sun. These planets also go through epicycles Observable - The Sun & planets follow a narrow path through the sky through 12 constellations (Zodiac). Mars, Jupiter, & Saturn move at a slower pace through the Zodiac than the Sun, Mercury, & Venus. The orbits of the planets and the Sun around the Earth are coplanar. Ma, J, Sa’s orbits around the Earth are exterior to that of the Me, V, & the Sun Observable - The Moon is seen to go through phases on an ~ 29-day cycle. The Moon orbits the earth & thus the percentage of the Moon’s surface illuminated by the Sun with respect to an observer on Earth changes New Belief - Heliocentric (SunCentered) Model • Copernicus (1473-1543): Credited for the Heliocentric Model • Tycho Brahe (1546-1601): Made accurate measurements of the positions of stars & planets • Johannes Kepler (1571-1630): interpreted Tycho’s data. His models supported the Heliocentric model of the solar system • Galileo (1564-1642): made use of a telescope to observe the phases of Venus & the moons of Jupiter Phases of Venus Old model. Venus would always be in a crescent phase Venus is not observed to always be in crescent phase • Galileo’s observations of the moons of Jupiter was crucial in showing that not all objects orbit the Earth. Heliocentric • • • • Observable - Mercury & Venus are always in close proximity to the Sun, and either trail or lead the Sun in the sky. M & V orbit the Sun on orbits interior to the Earth’s orbit around the Sun. Observable - Mars, Jupiter, & Saturn are not restricted to close proximity to the Sun, & are seen to make loops in the sky during opposition with the Sun. M, J, & S orbit the Sun on orbits exterior to the Earth’s orbit around the Sun. The loops result from Earth overtaking a planet in its orbit Observable - The Sun & planets follow a narrow path through the sky through 12 constellations (Zodiac). Mars, Jupiter, & Saturn move at a slower pace through the Zodiac than the Sun, Mercury, & Venus. The orbits of the planets around the Sun are coplanar. Observable - The Moon is seen to go through phases on an ~ 29-day cycle. The Moon orbits the earth & thus the percentage of the Moon’s surface illuminated by the Sun with respect to an observer on Earth changes The Zodiacal Constellations Motion of the outer planets Motion of outer planets • Retrograde motion: reverse of the normal direction. An apparent westward motion of a planet with respect to the stars, caused by the motion of the Earth • Opposition: The position of a planet when it is opposite the Sun in the sky The phases of the moon • The moon orbits the Earth (Period ~ 27 days) • The observed phases of the Moon are due to the relative positions of the Moon & Sun with respect to the Earth =b =a = 2a Ellipse • Ellipse: a set of all points, the sum of whose distance from 2 fixed points (the foci) is a constant • Thus, by the definition, • The ellipse is symmetrical about the foci. Thus, by considering the condition at which both angles equal zero Ellipse • From (B), it is thus clear that (A) • It is also true from (B) that, • and that (B) Ellipse • Rearranging the terms in the last two equations, squaring them, then adding them together, (A) Ellipse • Substituting, (A) • We get • And finally • Note that, when ! = 0, we have the distance of the pericenter, • When ! = 0, we have the distance of the apocenter Conic Sections • It turns out that • applies to any slice through a cone. • Ellipse ! 0 < e < 1 • Circle ! e = 0 • Parabola ! e = 1 (a = !" • Hyperbola ! e > 1 Kepler’s Laws of Planetary Motion • Each planet moves in an elliptical orbit about the Sun, with the Sun at one focus of the ellipse. • Equal areas of a planet’s orbit around the Sun are swept out in equal times • The cube of the distance from the Sun, a, divided by the square of the time, P, required to traverse the orbit is a constant, and is the same for every planet Useful units: Kepler’s 2nd Law • Equal areas are swept out in equal times. • From the figure, • The distance "r moved in time "t is • Element of the area swept out in "t is Kepler’s 2nd Law • Dividing both sides of • By "t, • I.e., angular momentum = mr2#, so Kepler’s second law is a result of conservation of angular momentum Newton’s 3 laws of motion • • 1) Kepler’s 3 laws are empirical. Kepler did not know the physics behind them. Newton provided the physical explanation of Kepler’s laws Newton’s Laws Law of inertia or law of conservation of linear momentum 2) Law of force 3) Action-reaction - balance of forces Newton’s 3 laws of motion 3) Action-reaction (cont). From conservation of total linear momentum, the initial momenta of objects 1 and 2 must be equal to the final momenta • Law of Gravity: Kepler’s 3rd law from Newton’s Laws • Consider 2 masses orbiting in circular orbits about their center of mass. The forces acting on m1 and m2 are Kepler’s 3rd law from Newton’s Laws • So, • Because • We can write Kepler’s 3rd law from Newton’s Laws • Substituting in for r1, • Solving for P and adopting m2 >> m1, Orbital Velocity • From before, we saw that • where $ab = area of an ellipse. Also, • So, • Lastly, from before, Orbital Velocity • What are the components of the velocity vector • For an ellipse, • such that • For the radial velocity component, Orbital Velocity • where, from differentiating the equation for an ellipse, we get, • Thus, • Rewriting the equation for an ellipse as • and recalling Kepler’s 3rd law, Orbital Velocity & Energy Equation • We get, • Note that the terms can be rearranged to get the energy equation Orbital Velocity • Two special cases: 1) Circular motion (r = a) & M* >> m, 2) Parabolic (a = !". The escape velocity is Orbital Properties • Kepler’s 3rd law: • The eccentricity of most of the orbits is ~ 0.0. I.e., planetary orbits are circular. • The inclination of most of the orbits is ~ 0o. • Bode’s Law?? Titius-Bode Rule (Bode’s Law) • Bode’s Law: • Plus - “Rule” developed before asteroid belt was discovered • Minus - No underlying physics. Neptune (& Pluto) do not fit