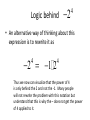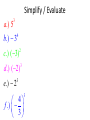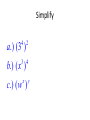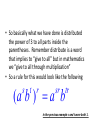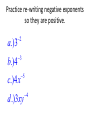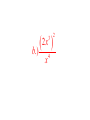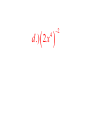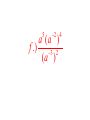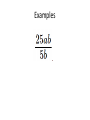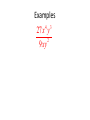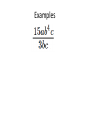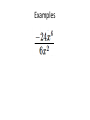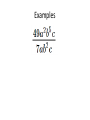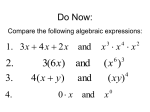Download 6.1 Multiplication with Exponents and Scientific Notation

6.1 Multiplication with Exponents and
Scientific Notation
6.2 Division with Exponents and
Negative Exponents
6.3 Operations with Monomials
6.1 Multiplication with Exponents
Recall that an exponent is a number placed
above and to the right of another number. The
other number is referred to as the BASE.
EXPONENT
b
BASE
x
• Exponents are sometimes referred to as
powers. “Special powers like ‘2’ have phrases
like ‘squared’ and ‘3’ has the phrase ‘cubed’”
Everything else we would say “the base raised
to that exponent”
KNOW THAT IF A POWER IS NOT WRITTEN THEN IT IS
AN UNDERSTOOD ONE “1”. AS YOU BEGIN DOING
THIS WORK IT MAY BE BENEFICIAL AT TIMES TO
PLACE A 1 WHEN IT IS NOT WRITTEN.
55
1
xx
1
Evaluating Exponents
Exponents simply tell us how many times we are
multiplying the base by itself.
So some examples: 53 means that we are
multiplying 5 by itself 3 times. 5 x 5 x 5.
EVALUATING tells us to find the equivalent value
of 53 which in this case would be 125.
Important Notation
• An exponent is intended to be applied only to
the base that it is directly behind. Therefore if
we have something like the following…
4
12 3
• The power of 4 only gets applied to the three.
So an equivalent statement would be
12 x 3 x 3 x 3 x 3 = 972
• Now if we were to incorporate a set of
parentheses in the same expression it changes
the way we think about what the power gets
applied to.
(12 3)
4
• Now the idea is that the power of 4 is applied
to the entire quantity inside the ( ) and not
just the 3. So this would be (36)4=1,679,616
• The biggest mistake that people make is in regards
to negative numbers and exponents.
• Recall that an even amount of negatives will always
give a positive product and an odd number of
negatives will yield a negative result. Take the two
examples below
(2)
4
In this example we are
viewing the -2 as an entire
quantity so that entire term
is raised to the 4th power.
we would get -2 x -2 x -2 x -2
2
4
In this example because there
Are no ( ) the power of 4 is only
To be applied to the thing that it
Is directly behind which is the 2.
NOT THE --
Logic behind
2
4
• An alternative way of thinking about this
expression is to rewrite it as
2  1 2
4
4
Thus we now can visualize that the power of 4
is only behind the 2 and not the -1. Many people
will not rewrite the problem with this notation but
understand that this is why the – does not get the power
of 4 applied to it.
Simplify / Evaluate
3
a.) 5
b.)  3
4
c.) (3)
2
d .) (2)
e.)  2
3
3
 4
f .)   
 3
3
Product Property
• Occasionally we will want to multiply bases that are the
same but both have exponents.
5 5
3
2
• The idea is that we can expand this to
5x5x5x5x5
How many 5’s do we have?
Can you look at the original problem and
determine a rule that would apply?
• So simply stated when we are multiplying
bases together that are “like bases” then we
add the exponents.
b b  b
r
s
r s
Simplify (leave answers in terms of
base with one exponent)
a.) 3  3
4
3
b.) 2  2  2
4
6
1
c.) 3  3  3  3  3
d .) x  x  x
2
4
e.) r  r  r
t
s
w
3
Power Property (sometimes called power
to a power)
• Lets use what we already know about
exponents to develop a rule for this.
2 3
(5 )
Focus on the red exponent first, what does that
mean?
2
2
2
(5 )(5 )(5 )
Now if multiplying like bases what do you do
with exponents?
6
5
So what is the rule?
• When a power is raised to another power we
simply keep the same base and multiply the
powers.
(b )  b
r s
r s
Simplify
4 2
a.) (3 )
3 4
b.) ( x )
x y
c.) ( w )
Distributive Property of Exponents
• This property comes in handy when an exponent is
being applied to a quantity that contains two or
more numbers or variables.
3
(4 y )
• The whole idea is based on what we already know.
4y 4y 4y
• But that also could be written as
4 y 4 y 4 y
• Which can be written as
444 y  y  y
• Which we can then change back to
3
4 y
3
• So basically what we have done is distributed
the power of 3 to all parts inside the
parentheses. Remember distribute is a word
that implies to “give to all” but in mathematics
we “give to all through multiplication”
• So a rule for this would look like the following
(a b )  a b
s t r
sr tr
In the previous example s and t were both 1.
Unless you have nested
parentheses then you want to
apply the power to power or
distributive properties first.
Understand that the distributive
property is simply an extension of
the power to a power rule.
Simplify
 1 3 2 
a.)   x y m 
 3

3 2
7
b.) ( w ) (2 w)
3
2 3
2
5
c.) (3 x y ) (2 xy m)
3 2 4
d .) (2( x ) )
3
Scientific Notation
• Scientific notation is a technique for writing
very large or very minute values. When
numbers incorporate many place values to
either side of the decimal, calculations can get
messy. Scientific notation is an attempt to
alleviate some of that “messiness”
• Scientific notation will always look like the
following.
n  10
r
• Where n is always a number between 1 and
10. And r is an integer (…-3, -2, -1, 0, 1, 2, 3…)
• When dealing with scientific notation and really
large or small values we will want to first locate
the current decimal point. Then the goal is to
move that decimal point so that it is between
the first two numbers that are non-zero values.
EXAMPLES
454, 000, 000
213, 000
5,321, 000, 000, 000
6.2 Division with Exponents and
Negative Exponents
• When multiplying like bases we ADDED
exponents.
• When dividing like bases we will now
SUBTRACT exponents.
3
4
2
4
• The idea is that you can expand the top and
bottom to the following
444
44
• And then reduce. Leaving just 4. That can be
more easily done by subtracting 3-2.
• When subtracting (at first at least) we will always
subtract so that our exponents are positive (biggersmaller) and then wherever the larger exponent
began is where our new total will go.
2
5
5
5
8
4
5
4
Negative Exponents
• If exponents are negative it means that we have a
fraction as an answer. For instance if we would have
taken the following and subtracted “top-bottom”
2
5
5
5
We would have gotten …
5
3
But we do not like negative exponents in answers, so we transition
The negative exponent and its base to the denominator and it becomes
A positive exponent.
Practice re-writing negative exponents
so they are positive.
2
a.)3
b.)4
3
c.)4 x
5
d .)3 xy
4
• Now from time-to-time we may end up with a
negative exponent that shows up in the
denominator of the fraction, if this occurs we take
the base and exponent that is negative and move it
to the numerator and make it positive. Examples.
1
a.) 2
4
2
b.) 2
x
1
c.)
3
3ab
• We do not like negative exponents in our answers,
whenever you have negative exponents to make
them positive exponents you must take the exponent
and the base that it belongs to and move them on
the other side of the division bar. (if you follow this
rule it doesn’t matter which order you subtract
exponents)
10
x
a.) 4
x
x5
b.) 7
x
21
2
c.) 25
2
Expanded Distributive Property
• If there is division occurring but the whole quotient
is raised to a power, you must distribute that power
to every exponent in the numerator, as well as every
exponent in the denominator.
x
a.)  
5
2
 2
b.)  7 
x 
3
c.)  
2
3
3
• Any base raised to the zero power is ALWAYS
simplified to equal 1.
• Here is an example of why, use your rules to
evaluate. But first make a determination of
what you get when you divide something by
itself.
3
5
3
5
Combining Properties
• A general practice, because its needed in
other areas, is to take all of these properties
and force you to work with them inside one
problem. We will do several examples.
• Get rid of parentheses first. So apply power to
powers first if present. Do division last, if
present. (ALWAYS WRITE ANSWERS WITH
POSITIVE EXPONENTS)
6
x
a.) 3 4
(x )
2x 

b.)
2
3
x
4
y 
c.)  3 
y 
8
2
d .)  2 x

4 2
6
e.) x  x
2
5
2 4
a (a )
f .)
3 2
(a )
Scientific Notation for Small Numbers
Here the numbers will have a decimal place out
front followed by several zeroes and then some
non-zero values. We will want to move the
decimal place so that it stops between the first
two non-zero values. Count the decimal places
moved and that will be your exponent.
However because we moved the decimal to the
right, the exponent will be negative.
Examples
.00004324
.0002
.0000982
.0032
*reminder explain why this works on the chalkboard
using negative exponents with the base of 10*
6.3 Operations with Monomials
• A monomial is a one-term expression that is
either constant (number “non-changing”) or
the product of a constant and one or more
variables raised to whole number exponents.
•

3
Here are some examples
15x
x y
2
23 x y
2
4
2 4
49 x y z
3 2 3
ab
4
• The number associated with monomials is called
the coefficient. A monomials are also referred to
as “terms”
• Rules for operating with monomials.
– Apply all rules that we learned about exponents
– Can only multiply / divide like terms (same base)
– Coefficients only work with coefficients
• Divide coefficients and multiply coefficients
• Commutative and Associative properties are
often useful when simplifying.
Examples
Examples
4
27 x y
2
9 xy
3
Examples
Examples
Examples
Multiplying and Dividing Numbers in
Scientific Notation
Multiplying  multiply the two numbers out in front, and then
add the exponents that go with 10. Re-write abiding by scientific
notation rules
Dividing  Divide the two numbers out in front, and then
subtract the exponents that go with 10. Re-write abiding by
scientific notation rules.
Examples
Examples
Examples
Two monomials with the exact same
variable part (same variables raised to
the exact same powers) are called
similar or like terms.
When adding and subtracting
similar/like terms you add/subtract
coefficients and that is all