* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson 96: Difference of Two Squares Theorem
Survey
Document related concepts
Transcript
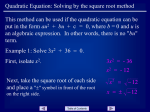
Bell Work: What are the four types of non-linear functions discussed in yesterday’s lesson? Answer: Quadratic, Cubic, Square Root and Absolute Value Lesson 96: Difference of Two Squares Theorem In Lesson 62 we introduced the topic of square roots and noted that every positive real number has both a positive square root and a negative square root. Because 2 times 2 equals 4 and -2 times -2 also equals 4, we say that the two square roots of 4 are +2 and -2. When we use the radical sign, √ , to indicate the square root of a positive number, we are designating the principal or positive square root. For example, √4 = 2 If we wish to indicate the negative square root, we must use a minus sign in front of the radical. For example, to designate the negative square root of 4, we must write -√4 which equals -2 If we are asked to find the numbers that satisfy the equation 2 x=4 We know that the numbers are +2 and -2 because 2 2 (+2) = 4 and also (-2) = 4 The general form of the 2 2 2 equation x = 4 is p = q . The theorem that describes the solution to an equation of the form p2= q 2 is called the difference of two squares theorem. Difference of two squares theorem: if p and q are 2 2 real numbers and if p = q, then p = q or p = -q. A quadratic equation in x has an x 2 term as the highest power of the variable. A quadratic 2 equation in p has a p term as the highest power of the variable. It is very important to realize that in the beginning of the book the ± sign arises only in the solution of a quadratic equation. For example, 2 if m = 3 then m = ±√3 Example: 2 Solve p = 16 Answer: p = ±4 Example: 2 Solve p = 41 Answer: p = ±√41 Example: 2 Solve k = 13 Answer: k = ±√13 HW: Lesson 96 #1-30