* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download line - Brenda Womack
Survey
Document related concepts
Transcript
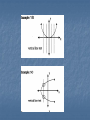
Strategies for Success GOOD LUCK!! Strategy 1 Can I plug it in? Strategy 2 Can I graph it? Strategy 3 Can I make a table of values? Strategy 4 Can I draw a picture? Function Each “x” is paired with exactly one y x cannot repeat The vertical line test can be used to determine whether a relation is a function How it’s tested Independent Variable The input or “x” variable Will be graphed on the “x” axis. Will be on the right side of the equation. Dependent Variable The output or “y” variable Will be graphed on the “y” axis Will be on the left side of the equation. C=40+25h Dependent Independent Variable Variable C O S T # of hours How it’s Tested Domain Set of allowable “x” values Range Set of allowable “y” values How it’s Tested What is the domain of this function? a) -3 < y < 3 b) -3 < y < 3 c) -3 < x < 3 d) -3 < x < 3 Correlation On overall pattern in the data of a scatterplot The three types of correlation tested on the TAKS are positive, negative, and no correlation. How it’s tested Mapping A pair of ovals which show how x and y are paired. x-intercept Point where graph touches x-axis Point will be written (a, 0) To find the x-intercept, plug in 0 for y and solve y-intercept Point where graph touches the y-axis Point will be written (0, b) To find the y-intercept, plug in 0 for x and solve. How it’s tested What is the x-intercept the function f(x) = 3x + 6 a) (6, 0) b) (0. 6) c) (0. -2) d) (-2, 0) Slope Indicates the steepness of a line Rise/Run Rate of Change y 2 y1 m x2 x1 How it’s tested What is the rate of change for the graph below? What is the slope of the equation 2x – 5y = 10? a) 2/5 b) 5/2 c) -2/5 d) -5/2 Parent Function The simplest form of a function family There will be two parent functions tested on TAKS: Linear and Quadratic How it’s tested Parameter Changes in Linear Functions In the linear function y = mx + b, m and b are called parameters. When the slope or “m” is changed, the only thing effected is the steepness of a line. When the y-intercept or “b” is changed, the line moves up or down the y-axis. How it’s tested The line y = ¾ x is drawn on a coordinate grid. A second line is drawn with a slope of 1. Which statement best describes the relationship between these two graphs? A) The second line is steeper than the first line B) The graphs are perpendicular lines C) The second line is less steep than the first line D) The graphs are parallel lines Parameter Changes in Quadratic Functions In a quadratic function of the form y = ax2 + c, “a” and “c” are called parameters. The value of “a” affects the width of the parabola Changing the value of “c” will cause a translation up or down. How it’s tested System of Equations Two or more linear equations that use two or more variables. The solution to a system is a pair of numbers that makes both equations true. On the TAKS, anytime you see two equations in the same problem, solve them both for y and then graph on your calculator. TAKS Examples: Systems TAKS Examples: Systems Roots, Solutions, Zeros The x-intercepts of a function Complementary Angles Two angles whose sum is 90 degrees a b Supplementary Angles Two angles whose sum is 180 degrees a b Dilation A proportional enlargement or reduction of a figure. The size of the enlargement or reduction is called the scale factor of the dilation If the dilated image is larger than the original, then the scale factor > 1. This is called an enlargement. If the dilated image is smaller than the original figure, then the scale factor < 1. This is called a reduction. Example Of Dilation Reflections A mirror image of a figure across a line. The line is called the line of reflection. A figure and its reflected image are always congruent. Translation A movement of a figure along a line Can be described by stating how many units to the left or right the figure is moved and how many units up or down it is moved. A figure and its translated image are always congruent Net A 2-dimensional representation of a 3dimensional object. How it’s tested Parallel Lines Two lines which have the same slope Perpendicular Lines Lines which intersect at 90 degree angles. Two lines whose slopes are negative reciprocals of each other. Similar Figures Same shape Corresponding Angles of similar figures are congruent The lengths of corresponding sides are proportional How it’s tested Right Triangles Use the Pythagorean theorem when you know 2 sides and need a 3rd Right Triangles Use the properties of special right triangles when you only know ________ side. Distance Formula Use whenever you need to find the length of a line segment. Midpoint Formula Use whenever you need to find the midpoint or “half-way” point of a line segment. Arc of a Circle Part of circle determined by any two points on the circle. The length of an arc is proportional to the circumference of the circle. The length of an arc can be found by setting up and solving a proportion. There are 360 degrees in a circle. Sector of a Circle Part of a circle bounded by two radii and an arc. Shaped like a piece of pie. The area of a sector of a circle is proportional to the area of the circle. Resetting the Memory Friendly Viewing Window When tracing functions on the graphing calculator, it is helpful to have a “friendly” viewing window. To obtain a “friendly” window, you must use multiples of 9.4 in the x min and x max. Zoom 6 When you want the “standard” 10 by 10 window, on your graphing calculator, press zoom 6. Zoom 0 Zoom Fit Window Use this window, to fit the function you have in y = . Table Setup Press 2nd Window to set up your table At TblMin tell the calculator where you want the table to start. At Tbl, tell the calculator what to go up by. Solve Algebraically, Confirm Graphically Solve Graphically, Confirm algebraically