Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Congruent Polygons
Document related concepts
Dessin d'enfant wikipedia , lookup
Integer triangle wikipedia , lookup
Euler angles wikipedia , lookup
Trigonometric functions wikipedia , lookup
Anatomical terms of location wikipedia , lookup
Four color theorem wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Tessellation wikipedia , lookup
Regular polytope wikipedia , lookup
Transcript
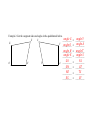
Congruent Polygons To name a polygon, start at any vertex and go around the figure, either clockwise or counterclockwise , and name the vertices in order. E M O Example 1: Give two (out of 12) possible names for the hexagon at the right. ____________________ DEMONS MEDSNO ____________________ D S N They have the same size and shape In simple terms, two polygons are congruent if _________________________________________________ _________________________ Their vertices can be paired so that corresponding More formally, two polygons are congruent iff _________________________________________________ angles and sides are congruent _______________________________________________________________________________________ Example 2. List the congruent sides and angles in the quadrilaterals below. πππππ π πππππ πΊ ο __________ __________ E S G Y __________ πππππ π΄ πππππ π ο __________ πππππ π __________ πππππ π ο __________ πππππ π πππππ πΈ ο __________ __________ O N T A πΊπ ππ΄ ο __________ __________ ππ π΄π ο __________ __________ ππΈ ππ ο __________ __________ πΈπΊ ππ ο __________ __________ When naming congruent polygons, you must list the corresponding vertices in order. This is known as a Congruent statement ____________________________________. YATS Example 3: Complete this congruence statement using the figure above: quad GONE ο quad __________ By looking at a congruence statement, you can determine the pairs of corresponding parts. Example 4: Use the statement ο CAT ο ο DOG to fill in the blanks. DO CA ο _____ G οT ο _____ ACT ο ODG ο _____ Example 5: V Given: VA ο VN O is the midpoint of AN VO ο AN VO bisects ο AVN Prove: ο AVO ο ο NVO A N O Statements Reasons 1. ______________________________ given 1. ______________________________ πππππ π΄ β πππππ π 2. ______________________________ Isosceles Triangle Thrm 2. ______________________________ π΄π β ππ 3. ______________________________ Def. of midpoint 3. ______________________________ Def. of perpendicular 4.πππ ______________________________ πππ΄ & πππ πππ = ππ‘. πππππ 4. ______________________________ 5. ______________________________ πππππ πππ΄ β πππππ πππ Right angle Thrm 5. ______________________________ 6. ______________________________ πππππ π΄ππ β πππππ πππ 6. ______________________________ Def. of angle bisector ππ β ππ 7. ______________________________ βπ΄ππ β βπππ 8. ______________________________ Reflexive 7. ______________________________ Def. congruent polygons 8. ______________________________
