Download Proving Statements in Geometry

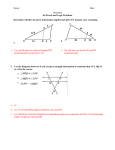
PROVING
STATEMENTS IN
GEOMETRY
WHAT IS A PROOF?
•A written account of the complete
thought process that is used to reach a
conclusion.
•Each step is supported by a theorem,
postulate or definition
WHAT IS IN A PROOF?
• A statement of the original problem
• A diagram, marked with “Given” information
• Re-statement of the “Given” information
• Complete supporting reasons for each step
• The “prove” statement as the last statement
– Sometimes Q.E.D. is written
• “quod erat demonstrandum” Latin for “which was to be demonstrated”
THE TWO COLUMN PROOF
STATEMENT
• Written on this side:
– Given statements (found
in the problem)
– Congruent statements
• Ex. 𝐴𝐵 ≅ 𝐵𝐶
REASON
• On this side
–Definitions
–Postulates
–Theorems
–Properties of shapes
YOU KNOW WHAT THEY SAY ABOUT
ASSUMING…
• Yes, you look at pictures.
• Yes, things will probably be drawn so that they look accurate.
• However, unless there are marks or written givens, you cannot
assume:
– Angles or segments are congruent
– An angle is a right angle
– Lines are parallel
– Lines are perpendicular
WITHOUT MARKS ON OUR
DIAGRAM OR WRITTEN WORD…
• We CANNOT assume...
• Lines a and b are parallel
• We CANNOT
assume...
• We CANNOT assume...
• Triangle ABC is a right
triangle
• M is the midpoint
of 𝐴𝐵
• 𝐵𝑀 ≅ 𝑀𝐴
PROPERTIES
• Reflexive property:
A segment or angles is congruent to itself.
AB  AB or A  A
•Transitive property:
If two or more segments or angles are
congruent to the same segment or angle, then
they are congruent to each other.
If 𝐴𝐵 ≅ 𝐶𝐷 and 𝐶𝐷 ≅ 𝐸𝐹 ,
then 𝐴𝐵 ≅ 𝐸𝐹
• Symmetric property: A congruence can be
stated in either order (congruence is
commutative)
If AB  CD, then CD  AB
PRACTICE
Name the property that is being used in the following
statements…
If RS  TW and TW  PQ ,
then RS  PQ
R  R
If N  M , then M  N
Transitive
Reflexive
Symmetric