Cusps, triangle groups and hyperbolic 3-folds
... two dimensions the signature formula (the Riemann-Hurwitz formula) gives complete information on the possible volumes of hyperbolic 2-orbifolds (the orbit spaces of Fuchsian groups). The situation is very different for hyperbolic 3-orbifolds: here there is no such formula, nor even a version of the ...
... two dimensions the signature formula (the Riemann-Hurwitz formula) gives complete information on the possible volumes of hyperbolic 2-orbifolds (the orbit spaces of Fuchsian groups). The situation is very different for hyperbolic 3-orbifolds: here there is no such formula, nor even a version of the ...
The Coarse Baum-Connes Conjecuture for Relatively Hyperbolic
... Definition (Cayley graph) Let G be a finitely generated group with generating set S = {s1 , . . . , sn }. The Cayley graph Cayley(G, S) is a graph (V, E) defined by V = G. E = {{g, g0 } : g−1 g0 ∈ S} ⊂ G × G. The coarse equivalent class of Cayley(G, S) does not depend on the choice of S. ...
... Definition (Cayley graph) Let G be a finitely generated group with generating set S = {s1 , . . . , sn }. The Cayley graph Cayley(G, S) is a graph (V, E) defined by V = G. E = {{g, g0 } : g−1 g0 ∈ S} ⊂ G × G. The coarse equivalent class of Cayley(G, S) does not depend on the choice of S. ...
Section 3
... the height of the Sears Tower in Chicago. He used a 12foot light pole and measured its shadow at 1 P.M. The length of the shadow was 2 feet. Then he measured the length of the Sears Tower’s shadow and it was 242 feet at that time. What is the height of the Sears Tower? ...
... the height of the Sears Tower in Chicago. He used a 12foot light pole and measured its shadow at 1 P.M. The length of the shadow was 2 feet. Then he measured the length of the Sears Tower’s shadow and it was 242 feet at that time. What is the height of the Sears Tower? ...
On right-angled reflection groups in hyperbolic spaces
... Hn have a common point at infinity. For a hyperface F of a polyhedron, we denote by H (F ) the closure of the hyperplane containing F in the compactification of Hn . Recall that two hyperplanes of Hn are called parallel if they do not intersect but their closures have a (single) point at infinity in ...
... Hn have a common point at infinity. For a hyperface F of a polyhedron, we denote by H (F ) the closure of the hyperplane containing F in the compactification of Hn . Recall that two hyperplanes of Hn are called parallel if they do not intersect but their closures have a (single) point at infinity in ...
The Geometry and Topology of Coxeter Groups
... Geometric realization of a poset Associated to any poset P there is a simplicial complex |P| called its geometric realization. Filling in Cay(W , S) Let W S denote the disjoint union of all spherical cosets (partially ordered by inclusion): a W S := ...
... Geometric realization of a poset Associated to any poset P there is a simplicial complex |P| called its geometric realization. Filling in Cay(W , S) Let W S denote the disjoint union of all spherical cosets (partially ordered by inclusion): a W S := ...
2-6 Proving Angles Congruent
... Supplementary Angles: two angles whose measures have a sum of 180. These angles may or may not be adjacent. See p. 96. ...
... Supplementary Angles: two angles whose measures have a sum of 180. These angles may or may not be adjacent. See p. 96. ...
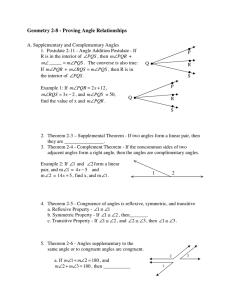
Sec 2.8: Proving Angle Relationships Description of the lesson: This
... iv. 2.12If two angles are congruent and supplementary, then each angle is a right angle v. 2.13 If two congruent angles form a linear pair, then they are right angles. 2) Closure a. Discuss what we did for this lesson i. What were some of our main ideas of this lesson 1. Congruence Properties for an ...
... iv. 2.12If two angles are congruent and supplementary, then each angle is a right angle v. 2.13 If two congruent angles form a linear pair, then they are right angles. 2) Closure a. Discuss what we did for this lesson i. What were some of our main ideas of this lesson 1. Congruence Properties for an ...
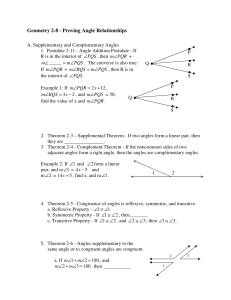
Geometry 2-8 - Proving Angle Relationships
... R is in the interior of ∠PQS , then m∠PQR + m∠ _____ = m∠PQS . The converse is also true: If m∠PQR + m∠RQS = m∠PQS , then R is in the interior of ∠PQS . Example 1: If m∠PQR = 2 x + 12 , m∠RQS = 3x − 2 , and m∠PQS = 50, find the value of x and m∠PQR . ...
... R is in the interior of ∠PQS , then m∠PQR + m∠ _____ = m∠PQS . The converse is also true: If m∠PQR + m∠RQS = m∠PQS , then R is in the interior of ∠PQS . Example 1: If m∠PQR = 2 x + 12 , m∠RQS = 3x − 2 , and m∠PQS = 50, find the value of x and m∠PQR . ...
Homework05 Solutions
... perpendicular to BC and AD . 4. Show that the diagonals are perpendicular if and only if all four sides are congruent, and in that case, , ABCD has an inscribed circle with center M. ( ⇐ ) Assume that all four sides are congruent. By SSS ΔDMC ≅ ΔBMC which implies that ∠DMC ≅ ∠BMC and since they are ...
... perpendicular to BC and AD . 4. Show that the diagonals are perpendicular if and only if all four sides are congruent, and in that case, , ABCD has an inscribed circle with center M. ( ⇐ ) Assume that all four sides are congruent. By SSS ΔDMC ≅ ΔBMC which implies that ∠DMC ≅ ∠BMC and since they are ...
Postulates Theorems and Corollaries 1. Midpoint Theorem If
... 3. Congruence of segments is reflexive, symmetric and transitive. 4. Angle Addition Postulate If R is in the interior of PQS, then mRQS + mPQR = mPQS. 5. Complementary angles are two angles with measures that have a sum of 90. 6. Supplementary angles are two angles with measures that have a sum ...
... 3. Congruence of segments is reflexive, symmetric and transitive. 4. Angle Addition Postulate If R is in the interior of PQS, then mRQS + mPQR = mPQS. 5. Complementary angles are two angles with measures that have a sum of 90. 6. Supplementary angles are two angles with measures that have a sum ...
Symmetric group
In abstract algebra, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutation operations that can be performed on n distinct symbols, and whose group operation is the composition of such permutation operations, which are defined as bijective functions from the set of symbols to itself. Since there are n! (n factorial) possible permutation operations that can be performed on a tuple composed of n symbols, it follows that the order (the number of elements) of the symmetric group Sn is n!.Although symmetric groups can be defined on infinite sets as well, this article discusses only the finite symmetric groups: their applications, their elements, their conjugacy classes, a finite presentation, their subgroups, their automorphism groups, and their representation theory. For the remainder of this article, ""symmetric group"" will mean a symmetric group on a finite set.The symmetric group is important to diverse areas of mathematics such as Galois theory, invariant theory, the representation theory of Lie groups, and combinatorics. Cayley's theorem states that every group G is isomorphic to a subgroup of the symmetric group on G.