Download Physics 136-3: General Physics Lab Laboratory Manual

Physics 136-3: General Physics Lab
Laboratory Manual - Waves and Modern Physics
Northwestern University
Version 1.1
December 8, 2016
Contents
Foreword
5
1. Introduction to the Laboratory
1.1 Objectives of Introductory Physics Laboratories
1.2 Calculus vs Non-Calculus Based Physics . . . .
1.3 What to Bring to the Laboratory . . . . . . . .
1.4 Lab Reports . . . . . . . . . . . . . . . . . . . .
.
.
.
.
7
7
8
8
8
.
.
.
.
.
.
.
.
.
11
11
12
12
14
15
16
20
21
23
3. Experiment 1:
Sound
3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
25
36
37
4. Experiment 2:
Snell’s Law of Refraction
4.1 Introduction . . . . . . . . .
4.2 The Experiment . . . . . . .
4.3 Part 2: Index of Refraction .
4.4 Analysis . . . . . . . . . . .
4.5 Conclusions . . . . . . . . .
.
.
.
.
.
39
39
41
42
46
46
5. Experiment 3:
Geometric Optics
5.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
49
64
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2. Understanding Errors and Uncertainties in the Physics Laboratory
2.1 Introduction: Measurements, Observations, and Progress in Physics .
2.2 Some References . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 The Nature of Error and Uncertainty . . . . . . . . . . . . . . . . . .
2.4 Notation of Uncertainties . . . . . . . . . . . . . . . . . . . . . . . . .
2.5 Estimating Uncertainties . . . . . . . . . . . . . . . . . . . . . . . . .
2.6 Quantifying Uncertainties . . . . . . . . . . . . . . . . . . . . . . . .
2.7 How to Plot Data in the Lab . . . . . . . . . . . . . . . . . . . . . . .
2.8 Fitting Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.9 Strategy for Testing a Model . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
CONTENTS
5.3
Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6. Experiment 4:
Wave Interference
6.1 Introduction . . . . . . . . . . . . . .
6.2 The Experiment . . . . . . . . . . . .
6.3 Analysis . . . . . . . . . . . . . . . .
6.4 Conclusions . . . . . . . . . . . . . .
6.5 APPENDIX: The Helium-Neon Laser
6.6 The Helium-Neon Laser . . . . . . .
6.7 Laser Safety . . . . . . . . . . . . . .
7. Experiment 5:
Diffraction of Light Waves
7.1 Introduction . . . . . . . .
7.2 Analysis . . . . . . . . . .
7.3 Conclusions . . . . . . . .
7.4 APPENDIX:
Intensity Distribution from
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
67
67
71
79
80
81
85
89
91
. . . . . . . . . . . . . . . . . . . . . . . . . . 91
. . . . . . . . . . . . . . . . . . . . . . . . . . 100
. . . . . . . . . . . . . . . . . . . . . . . . . . 102
a Single Slit . . . . . . . . . . . . . . . . . . . 102
8. Experiment 6: Intensity Distributions
of Diffraction Patterns
8.1 Introduction . . . . . . . . . . . . .
8.2 The Apparatus . . . . . . . . . . .
8.3 Analysis . . . . . . . . . . . . . . .
8.4 Conclusions . . . . . . . . . . . . .
8.5 APPENDIX:
The Semiconductor Diode Laser . .
8.6 The PIN Diode Photodetector . . .
9. Experiment 7:
Light Polarization
9.1 Introduction
9.2 Part 1 . . .
9.3 Analysis . .
9.4 Conclusions
.
.
.
.
.
.
.
65
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . . . . . . . . . . . . . . . 118
. . . . . . . . . . . . . . . . . . . . . 121
.
.
.
.
.
.
.
.
.
.
.
.
10. Experiment 8:
The Spectral Nature of Light
10.1 Introduction: The Bohr Hydrogen Atom
10.2 Analysis . . . . . . . . . . . . . . . . . .
10.3 Conclusions . . . . . . . . . . . . . . . .
10.4 APPENDIX: The Vernier Principle . . .
A. Physical Units
.
.
.
.
109
109
113
116
117
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
123
123
128
134
134
.
.
.
.
135
135
147
147
148
151
2
CONTENTS
B. Using Vernier Graphical Analysis
155
C. Using Microsoft Excel
157
C.1 Creating plots and curve fits . . . . . . . . . . . . . . . . . . . . . . . . . 157
C.2 Performing Calculations . . . . . . . . . . . . . . . . . . . . . . . . . . . 158
D. Using Microsoft Word
161
E. Submitting a Report in Canvas
163
3
CONTENTS
4
Foreward
Welcome to the general physics laboratory! This laboratory experience is designed to guide
your learning of fundamental concepts of experimentation and data collection, delivered
through the medium of hands-on experiments in electricity and magnetism. As a student,
you should be aware that you and your colleagues will have a broad set of backgrounds in
math, science, and writing and a similarly broad set of career trajectories. Even with the
diversity of participants in a course such as this, everyone can share an appreciation of the
scientific process. It is our job as instructors (TAs, faculty, and other assistants) to help
facilitate this learning independent of your preparation level. Some will find this easier than
others, but we will have done our job if you, regardless of background, walk away appreciating
a little more deeply what it means for a scientist to claim that “I know something” based on
experiments.
Some passages of text have been emphasized and color coded to make finding them later
more convenient.
Checkpoint
Checkpoints are intended to cause the student to be sure he is understanding and
remembering the material before continuing to waste his time.
Helpful Tip
Helpful tips offer the student an opportunity to learn a shortcut or otherwise to make
better use of his effort.
Historical Aside
A Historical Aside informs the student of some of the history associated with the
discussion topic. History itself is not helpful in performing the experiment or in
understanding the physics; however, it sometimes helps the student understand why
we do things as we do.
5
CONTENTS
WARNING
Warnings are exactly what they seem. Defying warnings can result in some personal
injury (likely not serious), in some disruption of the apparatus (time-consuming to
repair), etc.
General Information
General Information is usually very helpful with respect to understanding the
discussion topic in the broader context of the physical world.
We hope these decorations improve the student’s experience and help him/her to learn
to experiment more effectively.
6
Chapter 1
Introduction to the Laboratory
Physics is an experimental science. As part of basic education in Physics, students learn
both physical principles and problem solving (130/135 lecture) and concepts of experimental
practice and analysis (136). Physics 136-2 is designed to provide an introduction to experimental techniques in the laboratory, focused on experiments in electricity and magnetism.
We will build on the concepts covered in mechanics and use them to explain the indirect
observations of electric charges and currents. Since electricity itself is invisible, these studies
are considerably more abstract than students are accustomed; however, the process of using
a set of tools to yield data and then of analyzing the data to reach conclusions is the same.
The primary purpose of the Physics Laboratory is NOT to duplicate the concepts of lecture, although reinforcement is certainly beneficial and intended. This lab is an independent
course covering independent concepts. The topics of the lecture serve as examples that we
will explore in the lab to learn how to trust and to believe in physical principles. The schedule
of topics in each lecture may not correspond directly with the material in the lab, which
will be focused on measuring physical phenomena. These two components complement each
other, but they seldom track each other. Taken together, 130/135 and 136 should provide
the knowledge, problem solving skills, intuition, and practical experience with apparatus and
data collection expected of a first year in college-level physics.
1.1
Objectives of Introductory Physics Laboratories
In this course, students should expect to advance several learning goals that are broadly
relevant in science, technology, and general understanding of human knowledge. These
objectives are outlined by the American Association of Physics Teachers at
http://www.aapt.org/Resources/policy/goaloflabs.cfm:
• Develop experimental and analytical skills for both theoretical problems and data.
• Appreciate the “Art of Experimentation” and what is involved in designing and
analyzing a data-driven investigation, including inductive and deductive reasoning.
• Reinforce the concepts of physics through conceptual and experiential learning.
• Understand the role of direct observation as the basis for knowledge in physics.
7
CHAPTER 1: INTRODUCTION
• Appreciate scientific inquiry into creatively exploring how the world works.
• Facilitate communication skills through informative, succinct written reports.
• Develop collaborative learning skills through cooperative work.
1.2
Calculus vs Non-Calculus Based Physics
The same set of experiments are given to students in both calculus-based and algebra-based
physics courses. The work in this laboratory is designed to be independent of calculus, but
it is natural that students with more math background can better appreciate the subtleties
of the physics probed in these experiments. Calculus is never required in this course, and
your grading will not be affected by your knowledge of calculus (or lack thereof).
For completeness the physical laws and principles will be presented in their most general
form and that typically does require calculus; however, the student will receive the same grade
if he simply ignores these derivations and goes directly to the solutions. These solutions
frequently contain algebra and trigonometry but they can always be understood without
resorting to calculus.
1.3
What to Bring to the Laboratory
You should bring the following items to each lab session, including the first session of the
course. There is no additional textbook.
1) A bound quadrille ruled lab notebook. You must have your own, and you cannot
share with your lab partner. A suitable version is sold by the Society of Physics
Students in Dearborn B6. This lab notebook can be reused for future physics labs.
2) This Physics Laboratory 2nd Quarter lab manual. Accessing the online version on
a computer is acceptable in lieu of any printed copy, and likely preferable.
3) A calculator.
4) A pen.
5) You will need to transfer electronic data files and figures from lab to your lab
reports. This can be done by email, a cloud storage account, or you may prefer to
bring a USB drive to transfer from lab computers.
1.4
Lab Reports
You will write lab reports and submit them electronically. The purpose of this exercise is
both to demonstrate your work in lab and to guide you to think a bit more deeply about
what you are doing. The act of technical writing also helps improve your communication
skills, which are broadly relevant far beyond the physics lab.
8
CHAPTER 1: INTRODUCTION
The appendices of this lab manual provide some guidance on how best to prepare these
reports. You should keep in mind that these are not publishable manuscripts, but concise
and clear descriptions of your experiments. They will follow a clear format to communicate
your work best. They are not meant to be long. In the past, similar reports were written in
class in about 30 minutes. . . these at-home reports are a bit more involved than that, but not
by much. Students average one-two hours to complete them if their time in the laboratory
is optimized.
Each chapter of this lab manual describes what should be contained in your reports.
There are also opportunities for bonus points. Be certain to read these before class, since
they require additional lab work and cannot be accomplished during the writeup without
the necessary data.
9
CHAPTER 1: INTRODUCTION
10
Chapter 2
Understanding Errors and Uncertainties in the Physics Laboratory
2.1
Introduction: Measurements, Observations, and
Progress in Physics
Physics, like all natural sciences, is a discipline driven by observation. The concepts and
methodologies that you learn about in your lectures are not taught because they were first
envisioned by famous people, but because they have been observed always to describe the
world. For these claims to withstand the test of time (and repeated testing in future scientific
work), we must have some idea of how well theory agrees with experiment, or how well
measurements agree with each other. Models and theories can be invalidated by conflicting
data; making the decision of whether or not to do so requires understanding how strongly
data and theory agree or disagree. Measurement, observation, and data analysis are key
components of physics, equal with theory and conceptualization.
Despite this intimate relationship, the skills and tools for quantifying the quality of
observations are distinct from those used in studying the theoretical concepts. This brief
introduction to errors and uncertainty represents a summary of key introductory ideas for
understanding the quality of measurement. Of course, a deeper study of statistics would
enable a more quantitative background, but the outline here represents what everyone who
has studied physics at the introductory level should know.
Based on this overview of uncertainty, you will perhaps better appreciate how we have
come to trust scientific measurement and analysis above other forms of knowledge acquisition,
precisely because we can quantify what we know and how well we know it.
Scientific ideas themselves are not sacrosanct; contrarily, they can be replaced with improvements and refinements to understanding. This progress is measurable through analysis of
uncertainty in data, measurement, and calculation. Scientific progress is based on skepticism
and continued critical analysis; uncertainties guide us in our inquiries.
11
CHAPTER 2: UNCERTAINTIES
2.2
Some References
The study of errors and uncertainties is part of the academic field of statistics. The discussion
here is only an introduction to the full subject. Some classic references on the subject of
error analysis in physics are:
• Philip R. Bevington and D. Keith Robinson, Data Reduction and Error Analysis for
the Physical Sciences, McGraw-Hill, 1992.
• John R. Taylor, An Introduction to Error Analysis; The Study of Uncertainties in
Physical Measurements, University Science Books, 1982.
• Glen Cowan, Statistical Data Analysis, Oxford Science Publications, 1998
2.3
The Nature of Error and Uncertainty
Error is the difference between an observation and the true value.
Error = observed value - true value
The “observation” can be a direct measurement or it can be the result of a calculation that
uses measurements; in which case, the “true” value might also be a calculated result. Note
that according to this definition, an observation has an error even if we do not know what
the true value is. (Estimating this ‘true value’ is often the point of doing the experiment!)
Therefore, we will actually be analyzing the uncertainty, the estimate of the expected error
in an observation.
Example: Someone asks you, what is the temperature? You look at the thermometer
and see that it is 71◦ F. But, perhaps, the thermometer is mis-calibrated and the actual
temperature is 72◦ F. There is an error of −1◦ F, but you do not know this. What you can
figure out is the reliability of measuring using your thermometer, giving you the uncertainty
of your observation. Perhaps this is not too important for casual conversation about the
temperature, but knowing this uncertainty would make all the difference in deciding if you
need to install a more accurate thermometer for tracking the weather at an airport or for
repeating a chemical reaction exactly during large-scale manufacturing.
2.3.1
Sources of Error
No real physical measurement is exactly the same every time it is performed. The uncertainty
tells us how closely a second measurement is expected to agree with the first. Errors can
arise in several ways, and the uncertainty should help us quantify these errors. In a way the
uncertainty provides a convenient ‘yardstick’ we may use to estimate the error.
12
CHAPTER 2: UNCERTAINTIES
• Systematic error: Reproducible deviation of an observation that biases the results,
arising from procedures, instruments, or ignorance. Each systematic error biases every
measurement in the same direction.
• Random error: Uncontrollable differences from one trial to another due environment, equipment, or other issues that reduce the repeatability of an observation. They
may not actually be random, but deterministic (if you had perfect information): dust,
electrical surge, temperature fluctuations, etc. In an ideal experiment, random errors
are minimized for precise results. Random errors are sometimes positive and sometimes
negative; they are sometimes large but are more often small. In a sufficiently large
sample of the measurement population, random errors will average out.
Random errors can be estimated from statistical repetition and systematic errors can be
estimated from understanding the techniques and instrumentation used in an observation.
Other contributors to uncertainty are not classified as ‘experimental error’ in the same
scientific sense, but still represent difference between measured and ‘true’ values. The
challenges of estimating these uncertainties are somewhat different.
• Mistake, or ‘illegitimate errors’: This is an error introduced when an experimenter does something wrong (measures at the wrong time, notes the wrong value).
These should be prevented, identified, and corrected, if possible, and ideally they
should be completely eliminated. Lab notebooks can help track down mistakes or find
procedures causing mistakes.
• Fluctuations: Sometimes, the variability in a measurement from its average is not
a random error in the same sense as above, but a physical process. Fluctuations can
contain information about underlying processes such as thermal dynamics. In quantum
mechanics these fluctuations can be real and fundamental. They can be treated using
similar statistical methods as random error, but there is not always the desire or the
capacity to minimize them. When a quantity fluctuates due to underlying physical
processes, perhaps it is best to redefine the quantity that you want to measure. (For
example, suppose you tried to measure the energy of a single molecule in air. Due to
collisions this number fluctuates all over the place, even if you could identify a means
to measure it. So, we invent a new concept, the temperature, which is related to the
average energy of molecules in a gas. Temperature is something that we can measure,
and assign meaningful uncertainties to. Because of physical fluctuations caused by
molecular collisions, temperature is a more useful quantity in most cases.)
2.3.2
Accuracy vs. Precision
• Accuracy: Accuracy is how closely a measurement comes to the ‘true’ value. It
describes how well we eliminate systematic error and mistakes.
13
CHAPTER 2: UNCERTAINTIES
precise
accurate
precise
not accurate
not precise
accurate
not precise
not accurate
Figure 2.1: Several independent trials of shooting at a bullseye target illustrate the difference
between being accurate and being precise.
• Precision: Precision is how exact a result is determined without referring to the
‘true’ value. It describes how well we suppress random errors and thus how well a
sequence of measurements of the same physical quantity agree with each other.
It is possible to acquire two precise, but inaccurate, measurements using different instruments
that do not agree with each other at all. Or, you can have two accurate, but imprecise,
measurements that are very different numerically from each other, but statistically cannot
be distinguished.
2.4
Notation of Uncertainties
There are several ways to write various numbers and uncertainties.
• Absolute Uncertainty: The magnitude of the uncertainty of a number in the same
units as the result. We use the symbol δx for the uncertainty in x, and express the
result as x ± δx.
Example: For δx = 6 cm and a length L of 2 meters, we would write L = 2.00±0.06 m.
• Relative Uncertainty: The uncertainty as a fraction of the number.
Example:
0.06
δx
=
= 0.03
x
2.00
14
CHAPTER 2: UNCERTAINTIES
inches
centimeters
Figure 2.2: Measuring a string with a ruler. A reasonable measurements from this might
be reported as 7.15 ± 0.05 cm.
We must be very careful to say when our uncertainty is relative
x = 2.00 m ± 0.03(rel) = 2.00 m ± 3%
(2.1)
• Percent Difference:
The difference between measurements can sometimes be
represented as a percentage difference. The percentage difference between two values
x1 and x2 can be written as the difference divided by the average times 100% or:
Percentage difference = 200% ×
2.5
2.5.1
x1 − x2
x 1 + x2
(2.2)
Estimating Uncertainties
Level of Uncertainty
How do you actually estimate an uncertainty? First, you must settle on what the quantity
δx actually means. If a value is given as x ± δx, what does the range ±δx mean? This is
called the level of confidence of the results.
Note that the true value of a measurement does not need to fall in the range of the
uncertainty. This is a common misconception! In fact, for a 68% confidence interval, the
actual value does not fall in the range 32% of the time. In results of final measurements, it is
common to use 68%, 95%, and 99% confidence levels for reporting data, but unfortunately,
most practicing scientists are not always clear what they mean with an uncertainty. In
this course, we will follow the convention of 68% confidence intervals, so that δx
represents one standard deviation of the data set. Section 2.6 discusses the standard
deviation of a data set.
2.5.2
Reading Instrumentation
Measurement accuracy is limited by the tools used to measure. In a car, for example, the
speed divisions on a speedometer may be only every 5 mph, or the digital readout of the
odometer may only read down to tenths of a mile. To estimate instrumentation accuracy,
assume that the uncertainty is one half of the smallest division that can be unambiguously
15
CHAPTER 2: UNCERTAINTIES
read from the device. Instrumentation accuracy must be recorded during laboratory
measurements. In many cases, instrument manufacturers publish specification sheets that
detail their instrument’s errors more thoroughly. In the absence of malfunction, these
specifications are reliable; however, ‘one half of the smallest division’ might not be very
reliable if the instrument has not been calibrated recently.
2.5.3
Experimental precision
Even on perfect instruments, if you measure the same quantity several times, you would
obtain several different results. For example, if you measure the length of your bed with a
ruler several times, you might find a slightly different number each time. The bed and/or
the ruler could have expanded or contracted due to a change in temperature or a slightly
different amount of tension. These unavoidable uncertainties are always present to some
degree in an observation. Even if you understand their origin, the randomness cannot always
be controlled. We can use statistical methods to quantify and to understand these random
uncertainties.
2.6
Quantifying Uncertainties
Here we note some mathematical considerations of dealing with random data. These results
follow from the central limit theorem in statistics and analysis of the normal distribution.
This analysis is beyond the scope of this course; however, the distillation of these studies are
the point of this discussion.
2.6.1
Mean, Standard Deviation, and Standard Error
The mean: Suppose we collect a set of measurements of the same quantity x, and we
label them by an integer index i: {xi } = (x1 , x2 , . . . xN ). What value do we report from this
set of identical measurements? We want the mean, µ, of the population from which such a
data set was randomly drawn. We can approximate µ with the sample mean or average of
this particular set of N data points:
x̄ =
1 X
xi
N i
(2.3)
Of course, this is not the true mean of the population, because we only measured a small
subset of the total population. But it is our best guess and, statistically, it is an unbiased
predictor of the true mean.
The standard deviation: How precisely do we know the value of x? To answer
this question of statistical uncertainty based on the data set {xi }, we consider the squared
deviations from the sample mean x̄. The sample variance s2x is the sum of the squared
16
CHAPTER 2: UNCERTAINTIES
deviations divided by the ‘degrees of freedom’ (DOF). For N measurements the DOF for
variance is N − 1. (The origin of the N − 1 is a subtle point in statistics. Ask if you are
interested.) The sample standard deviation, sx , is the square root of the sample variance
of the measurements of x.
sP
N
2
i=1 (xi − x̄)
sx =
(2.4)
DOF
The sample standard deviation is our best ‘unbiased estimate’ of the true statistical standard
deviation σx of the population from which the measurements were randomly drawn; thus it
is what we use for a 68% confidence interval for one measurement.
The standard error: If we do not care about the standard deviation of a measurement
but, rather, how well we can rely on a calculated average value, x̄, then we should use the
standard error or standard
deviation of the mean sx̄ . This is found by dividing the sample
√
standard deviation by N :
sx
sx̄ = √
(2.5)
N
2.6.2
Reporting Data
Under normal circumstances, the best estimate of a measured value x predicted from a set
of measurements {xi } is given by x = x̄ ± sx̄ . If we perform N more measurements of
x, average them, and find their standard error, these two averages will agree within their
standard errors 68% of the time.
2.6.3
Error Propagation
One of the more important rules to remember is that the measurements we make have a
range of uncertainty so that any calculations using those measurements also must have a
commensurate range of uncertainty. After all the result of the calculation will be different
for each number we should choose within range of our measurement.
We need to learn how to propagate uncertainty through a calculation that depends
on several uncertain quantities. Final results of a calculation clearly depend on these
uncertainties, and it is here where we begin to understand how. Suppose that you have
two quantities x and y, each with an uncertainty δx and δy, respectively. What is the
uncertainty of the quantity x + y or xy? Practically, this is very common in analyzing
experiments and statistical analysis provides the answers disclosed below.
For this course we will operate with a set of rules for uncertainty propagation. It is
best not to round off uncertainties until the final result to prevent accumulation of rounding
errors. Let x and y be measurements with uncertainty δx and δy and let c be a number with
negligible uncertainty. We assume that the errors in x and y are uncorrelated; when one
value has an error, it is no more likely that the other value’s error has any particular value
or trend. We use our measurements as described below to calculate z and the propagated
17
CHAPTER 2: UNCERTAINTIES
uncertainty in this result.
• Multiplication by an exact number: If z = c x, then
δz = c δx
(2.6)
• Addition or subtraction by an exact number: If z = c + x, then
δz = δx
(2.7)
• Addition or subtraction: If z = x ± y, then
δz =
q
(δx)2 + (δy)2
(2.8)
• Multiplication or division: If z = xy or z = xy , then
v
u
δz u
δx
=t
z
x
!2
δy
+
y
!2
(2.9)
• Power: If z = xc , then
δz
δx
=c
z
x
(2.10)
The important pattern in these rules is that when you combine multiple uncertainties,
you do not add them directly, but rather you square them, add, and then take the square
root. The reason for this is intuitive: if one error is randomly positive, the other one is
sometimes negative, which reduces the total error. Therefore, it is incorrect to estimate the
combination of two uncertainties as their sum since this overestimates the average size of
the combined error.
3
As one example consider z = xy . Before we can use the division formula, Equation (2.9),
we must use the power formula to get the error in the numerator. Let w = x3 and use
Equation (2.10) to find that δw = 3w δx
= 3x2 δx. Next, Equation (2.9) gives our result
x
δz = z
v
u
u
t
δy
y
!2
δw
+
w
!2
=z
v
u
u
t
δy
y
!2
3 δx
+
x
!2
.
The exponent makes the numerator three times more sensitive to uncertainty than the
denominator.
18
CHAPTER 2: UNCERTAINTIES
2.6.4
Optional Reading – Advanced Topic:
The General Formula for Error Propagation
There is a general calculus formula encapsulating
the
rules for uncertainty propagation for a
general function of several variables A = f (x, y, z) . Derivation of this is beyond the scope
of this course. If you continue in your study of science, you will become more familiar with
equations like this.
δA =
2.6.5
v
u
u
t
∂f
∂x
!2
∂f
(δx)2 +
∂y
!2
∂f
(δy)2 +
∂z
!2
(δz)2
(2.11)
Significant Figures
The significant figures of a number are the digits in its representation that contribute to the
precision of the number. In practice, we assume that all digits used to write a number are
significant. Therefore, completely uncertain digits should not be used in writing a number
and results should be rounded to the appropriate significant figure. For example, you should
not express your height as 70.056 inches if your uncertainty is ±0.1 inch. It would more
appropriately be written as 70.1 inches. Uncertainties specified using only significant digits
are always ±5 times a power of 10; the least significant displayed digit was the result of
rounding up or down by as much as 0.5 of that digit. Usually we know our uncertainty to be
something close to this but yet different. Further, results of simple calculations should not
increase the number of significant digits. Calculations transform our knowledge; they do not
increase our knowledge. The rounding should be performed at the final step of a calculation
to prevent rounding errors at intermediate steps from propagating through your work but
one or two extra digits suffice to prevent this.
Zeros are also considered significant figures. If you write a number as 1,200, we assume
there are four significant digits. If you only mean to have two or three, then it is best to
use scientific notation: 1.2 × 103 or 1.20 × 103 . Leading zeros are not considered significant:
0.55 has just two significant figures.
There are some guidelines for tracking significant figures throughout mathematical manipulation. This is useful as a general method to keep track of the precision of a number so
as not to carry around extra digits of information, but you should generally be using more
formal error estimates from Sections 2.5 and 2.6 for reporting numbers and calculations in
the physics lab.
• Addition and Subtraction:
precise input number.
The result is known to the decimal place of the least
Example: 45.37 + 10 = 55, not 55.37 or 55.4
√
Why? δ = 0.0052 + 0.52 = 0.5
Where we used the sum formula Equation (2.7).
19
CHAPTER 2: UNCERTAINTIES
• Multiplication and Division: The result is known to as many significant figures
as are in the least precise input number.
Example: 45.4 × 0.25 = 11, not 11.4
r
Why? δ = 11
0.05
45
2
+
0.005
0.25
2
= 0.2 > 0.05
Where we used the product formula Equation (2.9).
Example: If you measure a value on a two-digit digital meter to be 1.0 and another
value to be 3.0, it is incorrect to say that the ratio of these measurements is 0.3333333, even
if that is what your calculator screen shows you. The two values are measurements; they are
not exact numbers with infinite precision. Since they each have two significant digits, the
correct number to write down is 0.33.
For this lab, you should use proper significant figures for all reported numbers. We will
generally follow a rule for significant figures in reported numbers: calculate your uncertainty to two significant figures, if possible, using the approach in Sections 2.5
and 2.6, and then use the same level of precision in the reported error and
measurement. This is a rough guideline, and there are times when it is more appropriate
to report more or fewer digits in the uncertainty. However, it is always true that the result
must be rounded to the same significant figures as the uncertainty. The uncertainty tells us
how well we know our measurement.
2.7
How to Plot Data in the Lab
Plotting data correctly in physics lab is somewhat more involved than just drawing points on
graph paper. First, you must choose appropriate axes and scales. The axes must be scaled
so that the data points are spread out from one side of the page to the other. Axes must
always be labeled with physical quantity plotted and the data’s units. Then, plot your
data points on the graph. Importantly, you must add your error bars to your data
points. Often, we only draw error bars in the vertical direction since these tend to dominate,
but there are cases where it is appropriate to have both horizontal and vertical error bars.
In this course, we use one standard deviation (standard error if appropriate for
the data point) for the error bar. This means that 68% of the time the ‘true’ value
should fall within the error bar range.
Do not connect your data points by lines. Rather, fit your data points to a model (often
a line), and then add the best-fit model curve to the figure. The line, representing your
theoretical model, is the best fit to the data collected in the experiment. Because the error
bars represent just one standard deviation, it is fairly common for a data point to fall more
than an error bar away from the fit line. This is OK! Your error bars are probably too large
if the line goes through all of them!
The fitting parameters are usually important to our experiment as measured values.
These measured parameters and other observations help us determine whether the fitting
20
CHAPTER 2: UNCERTAINTIES
model agrees or disagrees with our data. If they agree, then some of the fitting parameters
might yield measurements of physical constants.
More information can be found in Appendix B on page 155 and in Appendix C on
page 157.
2.8
Fitting Data
Fully understanding this section is not required for Physics 136. You will use least-squares
fitting in the laboratory, but we will not discuss the mathematical justifications of curve fitting
data. Potential physics and science majors are suggested to internalize this material; it will
become an increasingly important topic in upper division laboratory courses and research.
In experiments one must often test whether a theory describes a set of observations.
This is a statistical question, and the uncertainties in data must be taken into account to
compare theory and data correctly. In addition, the process of ‘curve fitting’ might provide
estimates of parameters in the model and the uncertainty in these parameter estimations.
These parameters tailor the model to your particular set of data and to the apparatus that
produced the data.
Curve fitting is intimately tied with error analysis through statistics, although the mathematical basis for the procedure is beyond the scope of this introductory course. This
final section outlines the concepts of curve fitting and determining the ‘goodness of fit’.
Understanding these concepts will provide deeper insight into experimental science and the
testing of theoretical models. We will use curve fitting in the lab, but a full derivation
and statistical justification for the process will not be provided in this course.
The references in Sec. 2.2, Wikipedia, advanced lab courses, or statistics textbooks will all
provide a more detailed explanation of data fitting.
2.8.1
Least-Squares and Chi-Squared Curve Fitting
For curve fitting, we make several measurements of a pair in a data set {xi , yi }, labelled by
an integer index i. We want to understand how well a theoretical curve predicts y given
x. Typically, we also want to extract some parameters {aj } in a model function f , such as
y = f (x, {aj }). The method to do this is based on the ‘method of maximum likelihood’,
which we do not cover in detail here. In words, we want to find the set of theoretical
parameters {aj } for a curve that maximizes the probability of obtaining the observed data
set {yi } from {xi }. This will be our best guess of the theory curve, and the result will be
an estimate of {aj }. Here, the index j is a different label than i: j labels the fit parameters
{aj } and i labels the data points {xi , yi }.
Let’s assume that there is no uncertainty in x, and we have N measurements of y, each
with some uncertainty. We have a set of N values yexp,i . We also have N predictions from
the theory curve ypred,i . These predictions may depend on unknown parameters {aj }. For
the least squares method, we ignore any error bars δyi and choose the parameters {aj } to
21
CHAPTER 2: UNCERTAINTIES
minimize the function
N
X
(yexp,i − ypred,i )2
(2.12)
i=1
This maximizes the probability of obtaining the measured data if the theory were correct.
Of course, it is possible that each measurement is not equally well known. Each data
point could have its own uncertainty δyi . In this case, we would minimize the variance with
each term weighted by how well we know it. This is called Chi-squared fitting and it is
the standard data fitting method used in physics laboratories. We seek to minimize some
function:
N
X
(yexp,i − ypred,i )2
(2.13)
χ2 =
δyi2
i=1
We allow the parameters {aj } to vary to give the smallest χ2 . This can be done in some
cases exactly from the data, and sometimes it needs an iterative procedure to find the best
fit solution. There are also procedures to extract the variance in the parameters {δaj } from
the method. Typically, software packages are used for this analysis.
2.8.2
Optional Reading – Advanced Topic:
Chi-Square ‘Goodness of Fit’
Suppose that we have a curve with given parameters {aj }. How well does it fit some
experimental data? There is a statistical test to determine the goodness of fit. We calculate
the χ2 statistic as above, and then divide by the degrees of freedom. If the parameters are
obtained from a fit, then the degrees of freedom is N − M where M is the number of fit
parameters. Basically, we use our N measurements to calculate the M parameters and the
DOF tells us how much ‘information’ we have left in our data set for optimizing the fit.
Think of it this way: If we had N independent fit parameters (unknowns) and N exact
data points (equations), we could in principle solve for all N unknowns. Instead we have
only M fit parameters so the problem is over-specified. On the other hand our data is also
uncertain so that we can use this over-specification to average out much of our uncertainties.
This is quite similar to making a measurement several times and then to average them to
get a better predictor for the ‘true’ value.
We calculate the reduced χ2 by dividing by the degrees of freedom. This statistic is
then compared to tables of numbers or using software to see how good the model fits the
data. If the uncertainties are correct, and the data is truly distributed as expected, and the
theory curve truly describes the underlying process, then the reduced χ2 should be about 1.
If it is larger, then there is too much variance and either the fit is bad or the uncertainties are
underestimated. If it is significantly less than 1, then the uncertainties may be overestimated
or the data might be insensitive to the variation predicted by the theory curve. The chisquare value should be near 1 for a properly fit theory curve correctly describing the physical
process with reasonable uncertainty estimates.
22
CHAPTER 2: UNCERTAINTIES
2.8.3
Example: Linear Regression
The optimization procedure is most often performed for a fit to a linear function y = mx + b.
Here, the two parameters that we wish to estimate are m and b, given a data set {xi , yi }
with N pairs. The best fit results can be derived using calculus:
m=
b=
xi y i − i xi i y i
P 2
P
N i xi − ( i xi )2
(2.14)
P 2P
P P
xi i yi − xi xi yi
P
P 2
2
(2.15)
N
P
P
i
N
i
xi − (
P
i
xi )
Assuming the uncertainties in y dominate and are all equal to δy, the variances can be
written:
2
=
σm
σb2
N
N
2
P
2 (δy)
2
i xi − ( i xi )
(2.16)
x2i
2
P
2 (δy)
2
x
−
(
x
)
i i
i i
(2.17)
P
P
=
i
N
P
The uncertainties of the parameter estimators are found from the square root of the variances.
The goodness of fit can be found from Equation (2.13). A proper statistical determination
of parameter uncertainties from real data in linear and nonlinear regression is a subtle topic
that is beyond the scope of this course.
2.9
Strategy for Testing a Model
Experiments are designed and performed for the purpose of testing whether we can rely
upon a particular hypothesis. Suppose we wish to check whether w = f (x, y, z) is a natural
truth. Then we must arrange to measure x ± δx, y ± δy, and z ± δz so that we can predict
the corresponding value of wp = f (x, y, z). We can also utilize what we have learned in
Section 2.6.3 to determine how the uncertainties δx, δy, and δz lead to the uncertainty in
our prediction δwp . Together, then we know that wp ± δwp if our model is correct.
We cannot quit there, however; just because the model made a prediction does not
necessarily mean it is correct. We must also arrange to measure wm ±δwm while our apparatus
is ‘set’ to x, y, and z. If the hypothesis is correct and our apparatus faithfully represents f ,
then this measurement must match f ’s prediction.
2.9.1
A Comparison of Measurements
If we make two measurements of (hopefully) the same quantity, both measurements contains
the inherent uncertainty of the tool(s) used to make the measurements. Then how can we
decide whether the two measurements agree? Statistics allow us to answer this question.
23
CHAPTER 2: UNCERTAINTIES
First, we form a null hypothesis by subtracting the two (hopefully equal) measurements
∆ = |wp − wm | .
(2.18)
Even if these two numbers were taken from the same population, this difference has expected
error, σ, due to δwp and δwm . We can find this error using our propagation formula for
difference (Equation (2.8))
σ=
q
(δwp )2 + (δwm )2 .
(2.19)
Since δwp already contains δx, δy, and δz, σ contains all of our measurement uncertainties
and we cannot reasonably expect ∆ < σ. Since our σ has 68% confidence level, we would
actually expect ∆ > σ to happen 32% of the time, ∆ > 2 σ to happen 4.6% of the time, and
∆ > 3 σ to happen 0.3% of the time. Larger disagreements are less and less likely.
Because of these statistics, we tend to consider when ∆ < 2 σ that the two numbers
agree, wp = wm , and that any minor discrepancy is more likely to be due to randomness
in the experiment and ‘other sources of error’. After all, claiming inequality would make us
wrong about once in twenty times; this is far too often for most scientists. On the other
hand, 3 in 1000 times is not too bad; we especially like these odds if they persist as we try
to reconcile the difference. Therefore we consider ∆ > 3 σ to indicate that the two numbers
disagree.
A disagreement could mean that the data contradicts the theory being tested, but
it could also just mean that one or more assumptions are not valid for the experiment;
perhaps we should revisit these. Disagreement could mean that we have underestimated
our errors (or even have overlooked some altogether); closer study of this possibility will be
needed. Disagreement could just mean that this one time the improbable happened. These
possibilities should specifically be mentioned in your Analysis according to which is most
likely, but further investigation will await another publication.
One illegitimate source of disagreement that plagues students far too often is simple
math mistakes. When your data doesn’t agree and it isn’t pretty obvious why, repeat your
calculations to make sure you get the same answer twice.
24
Chapter 3
Experiment 1:
Sound
3.1
Introduction
Sound is classified under the topic of mechanical waves. A mechanical wave is a term which
refers to a displacement of elements in a medium from their equilibrium state; but to be
a wave this displacement must then propagate through the medium. The speed at which
the wave propagates is inversely related to the mass density of the propagating medium and
directly related to the forces attempting to restore the equilibrium condition.
A mechanical wave can propagate through any state of matter: solid, liquid, and gas.
Mechanical waves can be of two types: transverse or longitudinal. A transverse wave is
characterized by a displacement from equilibrium which takes place at right angles to the
direction the wave propagates; longitudinal waves have the displacement from equilibrium
along the axis of propagation.
Since two directions are perpendicular to the direction of propagation, transverse waves
have two independent polarization directions. The form of the equations describing these
two types of waves is very similar. However, transverse waves can only exist in solid
media, where intermolecular bonds prevent molecules from sliding past one another easily.
Such sliding motion is called shear. Solids support shear forces and will spring back rather
than continue to slide; this intermolecular connection will transmit the transverse wave from
molecule to molecule.
Longitudinal waves rely only on pressure and can exist in both solids and fluids. They
depend on the compressibility of the media. Solids and fluids all show a resistance to compression. Sound waves are longitudinal waves that are transmitted as a result of compression
displacement of molecules of the medium. We usually discuss sound in air, but sound travels
in everything except empty space. A sound wave can be generated in solids, liquids, or gasses
and can continue to propagate in a different medium.
The equation used to describe a simple sinusoidal function that propagates in space is
given by
h
i
Y(x, t) = A0 sin k(x − vt) p̂
(3.1)
25
CHAPTER 3: EXPERIMENT 1
where Y is the time and position dependent displacement of the media from equilibrium,
A0 is the maximum displacement or amplitude of the medium’s motion, v is the velocity of
the wave which depends on the characteristics of the media. This particular wave travels
along the x-axis. . . x must increase at speed v to keep up with vt. p̂ is the polarization of
the wave. The case a longitudinal wave has p̂ = x̂ and a transverse wave has p̂ = py ŷ + pz ẑ
some combination of y and/or z polarization. k is a constant that is determined by both the
speed of the wave and the frequency of the wave. The constant k is usually expressed as
k=
2π
,
λ
(3.2)
where λ is the wavelength. The wavelength is related to the wave velocity v and the wave
frequency, f , by the expression
v = λf.
(3.3)
A periodic mechanical wave is characterized by a frequency of oscillation, f , which is
determined by the source of vibration motion that creates the disturbance. Thus, the
frequency and the speed of the wave in the media determines the wavelength. The source
can choose to oscillate at any frequency it chooses, but the medium decides the velocity of
propagation.
Checkpoint
What is the difference between a displacement wave and a pressure wave?
Checkpoint
Is sound a displacement wave, a pressure wave, or may it be considered as both?
Equation (3.1) describes the oscillations of particles with equilibrium position x. These
equations describe either longitudinal or transverse waves. The difference lies in the interpretation of the displacement which is described in the equation. For a transverse wave,
Equation (3.1) describes oscillations of the y and/or z coordinates of the particles at x.
For transverse waves the actual wave looks very similar to the plot of the displacement and
is easily visualized. For a longitudinal wave, Equation (3.1) describes oscillations of the x
coordinate of the particles at x in equilibrium. This results in a sinusoidal variation in the
density of media along the axis of propagation. This generally is much harder to visualize,
and there are few natural examples that can be easily observed. One such example would
be the pulse of compression which can be generated in a slinky spring.
A sound wave is a longitudinal wave and since the displacement of the wave causes a
variation in the density of air molecules along the direction of the wave, it can be viewed as
either a displacement wave or a pressure wave. The above equation may be used to describe
either picture. The displacement maximum is usually 90 degrees out of phase with the
26
CHAPTER 3: EXPERIMENT 1
Pressure Wave
(a)
(b)
(c)
Displacement Wave
Figure 3.1:
An illustration of the two representations of a longitudinal wave. The
displacement representation is the position of particles with respect to their average positions,
but the pressure increases as the particles move toward each other (compression) and
decreases as the particles move away from each other (rarefaction). The displacement wave
leads the pressure wave by 90◦ .
pressure maximum as shown in Figure 3.1. A sound wave is shown with both displacement
and pressure representations. The picture represents the density of the medium as the wave
passes through it.
Checkpoint
What determines the pitch of a sound wave? The source, the medium? Which
determines the speed of sound, the sound generator, the medium, or both? Which
determines the wavelength of sound, the sound generator, the medium, or both?
3.1.1
Superposition
When two sound waves happen to propagate into the same region of a medium, the instantaneous displacement of the molecules of the medium is normally the algebraic sum of the
displacements of the two waves as they overlap. If at one time and place each individual
wave would happen to be at a maximum amplitude, say Y1max and Y2max the net result would
be a displacement of the medium at a value equal to the sum of Y1max and Y2max . This is
27
(a)
Y1 + Y2
Y2
Y1
CHAPTER 3: EXPERIMENT 1
(c)
(b)
Figure 3.2: An illustration of constructive interference. Y1 and Y2 are in phase at all times
so that their sum has amplitude equal to the sum of Y1 ’s and Y2 ’s amplitudes.
(a)
Y1 + Y'2
Y'2
Y1
shown in Figure 3.2. If on the other hand, the second wave were at Y20max = −Y2max , the
net displacement equal to the sum of Y1max + Y20max , which in effect would be the difference
Y1max − Y2max or zero if the amplitudes are equal, as shown in Figure 3.3.
(c)
(b)
Figure 3.3: An illustration of destructive interference. Y1 and Y2 ’ are out of phase by 180◦
or half a wavelength. The sum of the two waves is zero if the two amplitudes are equal.
Checkpoint
What happens when two sound waves overlap in a region of space?
3.1.2
Reflection
We most often think of a reflection as occurring when a wave encounters the border of the
medium in which it is traveling. Anytime a wave encounters a sharp change in wave velocity,
due to a change in the nature of the medium, a reflection is generated and some or all of
the energy of the wave is redirected to the reflected wave. The amplitude and phase of the
reflected wave is determined by the boundary conditions at the point of reflection.
28
CHAPTER 3: EXPERIMENT 1
In this lab, we will consider the effects of reflection from a solid boundary, such that the
boundary condition requires that the sum of the waves have a displacement of zero at the
point of reflection. Air molecules cannot be displaced from equilibrium at the wall. They
cannot move into the wall and atmospheric pressure presses them into the wall; they simply
have nowhere to go. This condition can only exist if we were to superpose a second wave
moving in the opposite direction with exactly the same amplitude, and 180 degrees out of
phase with the original wave. Hence, in order to satisfy the boundary condition, a reflection
wave is generated with exactly these properties.
Pressure
0.97
0.47
(a)
-0.03
AN
N
AN
N
-0.53
AN
N
AN
N
-1.03
(b)
(c)
Wall
The resulting superposition of incident and reflected
waves in the region in front of
the boundary also sets up a
second null area where the amplitudes cancel at a distance
of one half of a wavelength
from the boundary as shown
in Figure 3.4. The null areas are called nodes. If the
wave didn’t loose amplitude
as it traveled, a null would
be present at successive half
wavelength intervals over the
entire region. As it is, the
wave looses amplitude as it
propagates, and the cancellation is only partial.
0.97
0.47
(d)
-0.03
AN
-0.53
-1.03
N
AN
N
AN
N
AN
N
Displacement
Figure 3.4: Illustrations of pressure waves and displacement waves reflected at a wall. The incident wave and
reflected waves interfere to produce a series of nodes (N) and
anti-nodes (AN) spaced every half wavelength. (a), (b), and
(c) are pressure standing waves and (d) is the displacement.
The pressure in (b) becomes the pressure in (c) after the gas
moves like the arrows between indicate. The gas ‘sloshes’
back and forth between the dotted lines, but on average does
not cross them.
29
The same boundary does
not place such restrictions on
the pressure wave. The pressure at the boundary may
rise and fall, as is required.
The wall can easily support
whatever pressure results from
the superposition of any two
waves. A suitable pressure
wave which takes advantage
of the boundary restriction
(which is none) is directed in
the opposite direction with an
equal amplitude to conserve
energy, and is in phase with
the incident wave. The resulting superposed waves show a
maximum or anti-node at the
CHAPTER 3: EXPERIMENT 1
boundary (see Figure 3.4) and a null point or node at a distance of one quarter wavelength
away from the boundary. If the amplitude is sustained as the wave travels, a second null
appears a half wavelength from the first, or at a point three quarters of a wavelength from the
boundary. Between each node, the wave is seen to oscillate between maximum positive and
maximum negative amplitudes, where the maximum amplitude is the sum of the maximum
amplitudes of the waves considered separately. These areas are called anti-nodes. Such a
wave is referred to as a standing wave because it stands still. In either case, successive null
points or nodes occur at intervals of half of the wavelength of the traveling waves.
By measuring the distance between nodes of the standing wave, we can determine the
wavelength of the incident and reflected traveling waves. Since we also know the frequency
at which we excited the wave, we can find the speed of the wave.
3.1.3
Part 1: Measuring the Speed of Sound in Air
From personal experience one can get a sense that the speed of sound in air is rapid. You
notice no delay in hearing a word that is spoken by a person nearby and the movement of the
speaker’s mouth. That would be quite a distraction, like watching a movie with the sound
track out of synch! And yet, when you sit in the outfield bleachers at a baseball game, you
can sense a noticeable delay between the arrival of the light showing the ball being hit and
the sound of the crack of the bat on the baseball.
The speed of sound is noticeably slower than the speed of light over distances the size
of a baseball field. In principle one could measure the speed of sound by timing how long
after ones sees the ball hit that the sound arrives if one knew how far away they were from
home plate. Instead, we will employ an oscilloscope simulation to observe the very short
time delay as sound travels a distance on the order of a meter.
In this experiment, a signal generator is used to produce a repeating electrical pulse to
drive a speaker. The pulse causes the speaker to emit a ‘click’ or pulse of sound whose speed
we will measure. A small microphone is used as a sensor. Its output is connected to one
input of the oscilloscope. The wave generator signal is also fed directly into the oscilloscope.
This signal will serve as a time reference against which to compare the microphone signal.
The delay introduced due to the distance in air that the sound travels from the speaker to
the microphone could be used to measure the speed of the click. Are the delays introduced
to the process of converting the electrical signal to mechanical sound and back, and in the
travel of electrical signals through the wire negligible? They probably are; however, we do
not have an exact location for where the sound is produced in the speaker or sensed in the
microphone. This could be a problem which we must deal with.
A sound wave will be sent down a tube and be reflected off a piston head back to a
microphone. We will measure the speed of the sound wave by observing the amount of time
delay that is introduced to the arrival of the echo as the distance between the speaker (and
microphone) and the piston head is increased. This way we do not need to know exactly
where the sound originates or is detected. If the position of the speaker and microphone are
unchanged, the only contribution to time is piston position.
30
CHAPTER 3: EXPERIMENT 1
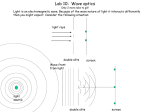
Figure 3.5: A sketch of the apparatus we will use to measure the speed of sound in air. A
wave generator and speaker will create a wave that travels down a tube and reflects from a
piston. A computer senses the travel time for the wave.
Helpful Tip
To avoid unnecessary interference with the measurements of other lab students, and to
spare the hearing and sanity of your Lab Instructor, leave your speaker on for ONLY
those times you are making measurements.
Set-up:
Familiarize yourself with the equipment as shown in Figure 3.5. Pasco’s 850 Interface will be
used to supply signals to the speakers from “Output 1”, to supply power for the microphone
from “Output 2”, to digitize the speaker’s signal, and to digitize the microphone’s output
in “Voltage D”. Check these connections. A suitable configuration for Pasco’s Capstone
program (“Sound 1.cap”) can be found on the lab’s website at
http://groups.physics.northwestern.edu/lab/sound.html
Click the “Monitor” button at the bottom left to start taking data.
Observe the two signals from A and B inputs displayed at the same time. Are the two
signals in phase? You may have to readjust the voltage scale to see the complete sine wave
of the microphone. Note the relative phase relation by drawing the two signals in your Data.
Be sure to label which is which.
31
CHAPTER 3: EXPERIMENT 1
Measure the Speed of Sound
To measure the speed of sound we want a square wave output and a frequency of about
5 - 20 Hz. To adjust the signal, click “Hardware” at the left and change only the frequency
for “Output 1”.
Figure 3.6: A sketch of the oscilloscope display showing the microphone’s response to
square wave ‘clicks’. The sound reflects off of the tube ends and travels back and forth down
the tube. The microphone measures each time the click passes by.
The pulse generated by the speaker travels down the tube and reflects off the moveable
piston back to the microphone. Drag the vertical numbers away from zero until the microphone signal occupies most of the Scope. Set the moveable piston to 80 cm from the speaker.
As you move the piston note that part of the signal moves to the right; these are the clicks’
echoes passing the microphone as the sound bounces back and forth. Drag the time numbers
to the right until the first echo observed by the microphone is near the right side of the
Scope and t = 0 is at the left side. You should see something similar to the display shown
in Figure 3.6. Move the piston closer to the mike.
Does the spike shift on the time scale? Sometimes it is hard initially to identify the
reflected pulse. It must move as the distance the clicks must travel changes and it must be
the first one to do so. The easiest way to identify the reflected click is to move the piston
around and to look for a pulse shifting around on the scope signal. As you move the piston
away from the mike you are introducing a delay in the time the microphone picks up the
32
CHAPTER 3: EXPERIMENT 1
sound. You might also see other peaks shifting as you move the piston. These may be second
and third echoes of the pulse bouncing off the speaker end of the tube.
Set the piston at some minimum distance for which you can readily observe the first echo
on the oscilloscope trace (20 cm is a good place). Note the piston position. How accurately
can you determine the piston’s position? Use the Smart Tool’s cross-hairs’ icon to locate
the leading edge of the pulse and note the time. Right-click the center of the SmartTool,
choose Properties, and increase the number of significant digits to 5-6. Be careful to write
the correct units and how accurately your time is known.
Now move the piston to a new position along the tube far from the speaker and note
the position again (70 cm is a nice choice. . . why?). Using the cross-hairs, determine the new
time of the shifted echo peak also. Remember that the extra distance you have introduced
to the sound travel is twice the change of position of the piston (going toward the piston
and coming back).
Calculate the speed of sound by dividing the extra distance added to the round trip of
the sound pulse by the corresponding increase in travel time. The pulse travels twice as far
as the piston moved but the oscilloscope measured the time (not double the time and not
half of the time),
2∆x
.
(3.4)
v=
∆t
The width of the echo’s leading edge can be an indicator of the uncertainty of the
measurement. If the echo moves around, this will increase your measurement error estimate.
Measure the latest time and subtract off the earliest time that might reasonably be assigned
to the time of the pulse’s echo. Let δ = latest - earliest and δt = 12 δ is a reasonable estimate
of the uncertainty in your time measurements. You need measure this uncertainty only once
since nothing substantial changes between measurements; each time measurement will have
this same uncertainty.
3.1.4
Part 2: Measuring the Wavelength Observing Standing Waves
Sound incident on a barrier will interfere with its reflection, setting up a standing wave near
the reflector. The distance between nodes in the standing wave is a measure of half the
wavelength of the original sound wave when the wave travels at right angles to the reflector.
Because of the inefficiency of the reflector and other losses, the nodes may be only partial
nodes. Additionally, the microphone has a finite size and will average the sound intensity over
a range of positions where only one position is at the intensity minimum. The wavelength of
sound should be expected to be on the order of meters for audible sounds. Diffraction effects
are commonly observed for sound waves passing through apertures like doors and windows
on the order of meters in size.
For this part of the experiment adjust the acrylic tube so there is about a centimeter gap
between the speaker and the end of the tube. This will release the pressure in the tube and
33
CHAPTER 3: EXPERIMENT 1
force this end of the tube to atmospheric pressure; this end will be a pressure node (and a
displacement anti-node). This part of the experiment will use “Sound 2.cap” that can be
downloaded from the lab’s website at
http://groups.physics.northwestern.edu/lab/sound.html
Set the frequency of the generator to 450 Hz. Click “Signal Generator” at the left to
access “Output 1” control panel. Keep the microphone near the piston and move the piston
and microphone to where the sound resonates in the tube (the microphone output goes to a
maximum).
Use the mike as a probe to measure the intensity of sound in the region between the
speaker and the piston by noting the amplitude of the signal on the scope as you move the
mike around back and forth inside the tube. This is the sound pressure level (SPL) as a
function of position, P (x), for the standing wave.
Place the mike near the piston and note whether the piston head is a node or an anti-node
by observing the variation in the intensity of the sound as you move the mike around near
the piston. Note your observation in your notebook. What would you expect for a pressure
wave or a displacement wave? Is the microphone a pressure sensor or an amplitude sensor?
Place the microphone near the speaker end of the tube, and note whether this is a maximum
or minimum. Explain this result in your notebook. You would think that near the speaker
you would get a large response from the microphone. Is that what you see?
Now, move the microphone to locate the first node away from the piston (remember that
right next to the piston is a displacement node) where the microphone’s output goes through
a maximum. Start with the mike right near the piston and move it away from the piston
and toward the speaker. Measure the first position of maximum response away from the
piston. Can you detect the next node? A third node? Record your observations. Record
the positions of the microphone where its output is minimum. Don’t forget your units and
error estimates; how accurately can you position the microphone at the maxima/minima and
how accurately can you read the centimeter scale? Move the microphone and remeasure one
node and one anti-node several times to check your error estimates. Are nodes and anti-node
measurements equally precise?
Calculate the wavelength of the sound from the distance between the first node of the
standing wave and the second node. If the nodes are close together, you can skip a node,
measure the distance between two nodes, and divide by two to get a better accuracy. After
all, your measurement errors will be divided as well since the denominator will be twice as
large.
Calculate the speed of sound using the wavelength just determined and the frequency
from the signal generator’s LED display; use Equation (3.3). Note your results in your lab
book.
34
CHAPTER 3: EXPERIMENT 1
Checkpoint
The distance between successive nodes in a standing wave is a measure of what?
3.1.5
Part 3: Sound Speed at Several Frequencies
Set the generator to something low around 450 - 500 Hz. Verify that the gap between the
speaker and tube end is still about 1 cm. Keep the microphone near the piston and vary the
position of the piston and microphone to maximize the microphone response.
Place the microphone at the end of the tube nearest the speaker. Put the piston all the
way into the tube so that it is close to the mike. Slowly withdraw the piston and observe
the position where the piston produces a maximum sound intensity. Move the microphone
to get a maximum response and see if the piston’s location can increase the microphone’s
output. Repeat until the piston’s position remains constant. This is where the tube is in
resonance with that particular frequency. Note this piston position, its units, and your error.
The position of the microphone will not need to change again until the frequency changes.
Withdraw the piston further and note a second resonance position. How precisely can
you position the piston and measure its position? If you cannot see a second resonance the
wavelength of the sound may be too long and you will need to increase the signal frequency.
These successive resonance positions are the positions of nodes for the standing wave at
this frequency. Since the distance between nodes is half a wavelength, merely doubling this
distance and multiplying it by the frequency of the sound as read off the signal generator
display will determine the speed of sound.
Repeat the measurements of successive resonance positions for four higher frequencies.
Make a table of wavelengths, frequencies, and calculated sound speeds for each frequency.
Plot your data using Vernier Software’s Graphical Analysis 3.4 (Ga3) program. A suitable
configuration for Ga3 can also be downloaded from the lab’s website. Does the speed vary
systematically with frequency? Use Ga3 to determine an average speed v̄ and a standard
deviation sv by drawing a box around the data points and by using the Analyze/Statistics
feature. Compute the deviation of the mean sv̄ using
sv
sv̄ = √
N
What frequency has a speed most similar to the speed measured in Experiment 1? Your
measurement’s best predictor is vs = v̄ ± sv̄
35
CHAPTER 3: EXPERIMENT 1
Checkpoint
For a displacement wave reflecting off a solid wall is the boundary a node or an antinode in the resulting standing wave? For a pressure wave reflecting off a solid wall is
the boundary a node or an anti-node in the resulting standing wave?
3.1.6
Part 4: Spectral Content
The Fourier Transform
Most of us are familiar with the link between musical pitch and sound frequency. A soprano
voice has high pitch and high frequency whereas a bass voice has low pitch and low frequency.
Probably you have already noticed while performing Part 3 above that higher frequencies
have higher pitch. You might also have noticed how ‘boring’ a pure sine wave sounds. For
contrast, select the square and triangle waveforms for “Output 1”; use a frequency of a few
hundred Hz and select the different wave shapes. Which shapes have the most pleasant
sound? Record your observations in your notebook.
We now want to investigate the frequency content of sounds more closely. The “Sound
FFT.cap” from the lab’s website provides a suitable configuration for Pasco’s Capstone
program. This will perform a ‘fast Fourier transform’ (FFT) on the microphone’s signal
and the speaker’s excitation. In graduate school you will learn more thoroughly that the
Fourier transform identifies the frequency or spectral content of functions of time. Study the
response vs. frequency for various waveform shapes and note your observations in your data.
The square wave should have responses at all integer multiples of the signal generator’s
frequency (the fundamental frequency). The triangle wave should have only odd multiples
of the fundamental. The amplitudes decrease for higher multiples or harmonics. Try singing
a pure note into the microphone and noting the spectral content of your voice.
3.2
Analysis
Calculate the Difference between the speed of sound found using the two different methods,
∆ = |v1 − v3 | .
Combine the uncertainties in these two measurements using
σ=
q
(δv1 )2 + s2v̄
Discuss the similarities and differences between this difference and the computed errors.
What other subtle sources of error can you think of that might have affected your measurements. Communicate with complete sentences. Which measurement method gives the best
accuracy and how do you know?
36
CHAPTER 3: EXPERIMENT 1
3.3
Conclusions
What physical relations have your measurements supported? Contradicted? Which were not
satisfactorily tested? Communicate with complete sentences and define all symbols. What
values have you measured that you might want to know in the future? Include your units
and errors.
37
CHAPTER 3: EXPERIMENT 1
38
Chapter 4
Experiment 2:
Snell’s Law of Refraction
4.1
Introduction
In this and the following lab the light is viewed as a ray. A ray is a line that has an
origin but does not have an end. Light is an electromagnetic disturbance and, as such, is
described using Maxwell’s equations, which expresses the relationship between the electric
and magnetic fields in an oscillating wave.
Light propagates as a wave; yet, many optical phenomena can be explained by describing
light in terms of rays. In the model for light, rays in a homogeneous medium travel in
straight lines. This model is referred to as Geometric Optics and is a very elementary
theory. In this theory light travels from its origin at a source in a straight line, unless it
encounters a boundary to the medium. Beyond this boundary may be another medium
which is distinguished by having a speed of light different from the original medium. In
addition, light may be reflected at the boundary back into the original medium. A light ray
that returns to the original medium is said to be “reflected”. A ray that passes into the other
medium is said to be “refracted”. In most interactions between light and a boundary, both
reflection and refraction occur.
In order to frame laws that govern these phenomena we must define some terms. The
boundary between two media is defined as a surface. The orientation of a surface at any
specific point is characterized by a line perpendicular to the surface that we call the normal.
A ray may encounter a boundary at any arbitrary incidence angle. The angle of incidence
is measured with respect to the normal line. A reflected ray will have an angle of reflection
that is also measured with respect to the normal. The refracted ray will be oriented by the
angle of refraction measured between the ray and the normal to the surface.
Checkpoint
For geometric Optics what assumption is made about the nature of light?
39
CHAPTER 4: EXPERIMENT 2
What distinguishes the two media is that the speed of light is different from one medium
to the other. We define the index of refraction n to be the measure of how much different
the speed of light is in a certain medium from that of light through a vacuum. Light travels
through a vacuum at 299,792,458 m/s. This speed is thought to be a universal constant and
the highest speed allowed in nature as postulated in Einstein’s theory of Special Relativity.
We use the symbol c to represent this speed.
The index of refraction is a characteristic of the medium. It is the only thing that
distinguishes one medium from another in geometric optics. It is defined as the ratio of the
speed of light in a vacuum to the speed in a particular medium of interest,
n=
c
c
or v = .
v
n
(4.1)
Therefore, the value of the index of refraction is always greater than unity. Gasses have an
index of refraction close to 1 (nair = 1.00028), while for water the index is about 1.33 and
for plastic it is approximately 1.4. Depending on the type of glass the index of refraction of
glass can vary from 1.5 to 1.7.
Normally we might think that the index of refraction is a constant that is the same for
all light. The index of refraction actually depends on the frequency (color) of the light wave
to a small degree across the visible part of the spectrum and as such is different for different
colors of light. The rules for reflection of light are:
1) The angle of incidence is equal to the angle of reflection,
θ1 = θ10
(4.2)
where θ1 is the angle of incidence and θ10 is the angle of the reflected ray that
propagates in the same medium. (This is the commonly known rule, but this next
rule is rarely stated though equally important)
2) The incident ray, the reflected ray, and the normal to the surface, all lie in the
same plane.
Checkpoint
What is the law of reflection?
We will not formally investigate these rules in this lab although you will be able to observe
the phenomena of reflection as a side issue while performing this lab experiment. The rules
for refraction are not so obvious although they where well known to the ancients.
1) The first rule is often cited as Snell’s Law; it is:
sin θ1
n2
=
or n1 sin θ1 = n2 sin θ2 .
sin θ2
n1
40
(4.3)
CHAPTER 4: EXPERIMENT 2
where θ2 is the angle of refraction of the ray that is transmitted into the second
medium.
2) The incident ray, the refracted ray and the normal to the surface, all lie in the
same plane.
Checkpoint
What is Snell’s Law? What phenomenon does Snell’s Law describe?
In general the path of a light ray is reversible in that if a light ray were to be reversed it
would follow the same path. A ray traveling from a low index of refraction to a high index of
refraction will experience a bending toward the normal. However a ray passing from a high
index of refraction to a lower index will experience a bending away from the normal. The
angle of refraction will be larger than the angle of incidence. So, what happens when the
angle of refraction is greater than 90◦ for a given incidence angle. In this case light cannot
be transmitted through the interface and as such it is reflected totally. The efficiency for this
reflection is 99.99% (as compared to 95% for a typical silvered surface mirror). The largest
angle for which a ray will be transmitted is the critical angle. One can show that the sine
of this angle is the inverse of the ratio of the index of refraction of the first medium to the
index of the second medium. If the second medium is air (n = 1.00028), the sine of the angle
is effectively the reciprocal of the index of refraction of the first material.
Checkpoint
In optics angles are always measured with respect to what?
4.2
The Experiment
The experiment consists of a single thin bundle of light rays exiting a light box. This ray will
be incident upon various objects so that we may deduce whether the laws of reflection and
of refraction are obeyed by the interaction between the light and the objects. A picture of
the ray box is shown in Figure 4.1.
4.2.1
Part 1: Reflections
In this experiment you will use the Light Ray Box shown in Figure 4.1. It consists of a light
source and a Multi-slit Slide. The light source housing is mounted on a colored plastic base
in which it can slide back and forth. The utility of this feature will be explained in a future
experiment. The Multi-slit Slide is a flat square piece of plastic with notches cut into each
41
CHAPTER 4: EXPERIMENT 2
of the four edges. The Multi-slit Slide slips into a slot on the end of the ray box to create
rays of light. Choose the side with just one narrow notch and place that side down as you
slip the a Multi-slit Slide into place. A single narrow beam should be observed emerging
from the ray box. Place the ray box on the end of a sheet of paper provided, such that the
ray is projected onto the paper.
Draw a long line for the surface of a mirror
using the ruler. Construct the surface normal
90◦ from this surface line using the protractor
and the ruler. Position the flat side of the shiny
triangle exactly on the surface line. Carefully
slide the paper (and shiny triangle) so that the
ray from the ray box hits the shiny triangle at
Figure 4.1: A photograph of the light ray
the position of the surface normal. Carefully
box and the multi-slit slide that we will use
rotate the paper and mirror about a vertical axis
to investigate ray optics.
passing through the surface-normal intersection
and note the relation between the incident and reflected rays. If the mirror moves on the
paper, carefully reposition it before marking the ray positions. Now mark the positions of
one incident ray and its reflected ray. One point far from the mirror and the point where
the ray hits the mirror (and the surface normal) define each of the two rays. Remove the
triangle, draw the incident and reflected rays, and measure the incident and reflected angles.
Be sure to record your units and to estimate your experimental errors. How accurately
can you construct the surface normal? How accurately can you position the mirror on the
surface line? How accurately can you point the ray at the intersection between the surface
and the surface normal? How accurately can you mark the incident and reflected rays? How
accurately can you construct the rays from the three marks? How accurately can you position
the protractor? How accurately can you read the protractor? All of these contribute to your
measurement errors and must be considered while you contemplate your error estimates. Is
your angle of reflection equal to your angle of incidence? Are your error estimates large
enough to cover the difference? If not, repeat the experiment more carefully.
4.3
Part 2: Index of Refraction
In this experiment you will also use the Light Ray Box shown in Figure 4.1. Locate the oddly
shaped Lucite block. Place the block on the paper with the frosted side down. Aim the ray
at one of the two parallel sides of the block. Note that the ray emerges from the opposite
side of the block in a direction parallel to the original ray but displaced slightly due to the
refraction of the ray inside the block. One option is to print the template in Figure 4.4 and
to use it instead of constructing everything on a blank page.
You will now draw lines representing the incident and refracted rays so that you can
measure the angle of incidence and refraction for several angles of incidence. Arrange the
block for a specific angle of incidence. You will repeat the following steps through a series
of five angles from a shallow angle to a steep angle of incidence.
42
CHAPTER 4: EXPERIMENT 2
Use a pencil or pen and a ruler to
draw a long line to represent the surface of
incidence. Use the protractor to construct
a surface normal perpendicular to the first
line. (Alternately, the worksheet following
these instructions may be photocopied or
removed and used directly.) Place the Lucite
block’s surface exactly on the first line and
carefully slide the paper and block (friction
Figure 4.2: A sketch of light refraction at the
will move the Lucite if the paper is moved
surface of a Lucite block. The ray enters the
without sudden jerks) so that the light ray
block at angle θ1 from the surface normal and
enters the Lucite above the intersection of
is refracted to angle θ2 from the same normal.
the surface and the normal constructed earBy noting the point the ray enters the block
lier. It might be possible to improve the
and exits the block, we have two points on the
length of the rays or their brightness by
line of the refracted ray.
elevating the front or back of the light ray
box with the ruler and/or protractor. Mark the location of the incident ray at another point
along the ray, such that its direction can be recreated later. It is advisable that this point
be near the ray box. Lastly, draw a two points on the opposite side of the block where
the ray emerges. These points should be separated as far as possible to make reproducing
the ray’s angle as accurate as possible. These points should be sufficient to recreate the
geometry of the refraction. Label these points “1” and carefully drag the paper and Lucite
block to set another incident angle with the ray once again entering the Lucite block at
the location of the normal line. Mark the incident and refracted rays as before and label
them “2”. Continue to mark three more rays for a total of five or more. If the Lucite block
should move off of the surface line, carefully reposition it before marking the refracted ray.
Remove the block and draw lines representative of the incident and refracted rays. On the
refracted side, construct the line between each pair of points and extend it back until it
intersects the Lucite block’s back surface. This is the point where the ray emerged from the
Lucite block, so inside the block the ray proceeded from O in a straight line to this point
of emergence. Connect O to this point of emergence with the ruler and extend the line to a
length that will allow you to use the protractor to measure its angle from the normal. Use
a protractor to measure the incidence and refraction angles; keep in mind that these angles
must be measured from the normal line and not from the surface. Record these measured
angles in a properly formatted table. Be sure to include the units and error estimates for
these measured angles. How accurately can you position the Lucite block along the surface
line? How accurately can you point the ray at the surface normal? How accurately can you
mark the incident and refracted rays? How accurately can you construct the incident and
refracted rays through the points that mark the rays? How accurately can you position the
protractor? How accurately can you read the protractor? All of these questions should be
considered while you are considering the sizes of your angle errors.
Order the results in a table in your lab book from smallest to largest angle. Plot the index
of refraction as a function of increasing incident angle using Vernier Software’s Graphical
Analysis 3.4 (Ga3) program. Your lab instructor will show you how to use the program if
43
CHAPTER 4: EXPERIMENT 2
you haven’t already used it in previous labs. GAX can also calculate your index of refraction
in a “calculated” column.
Observe if there are any systematic changes in the index of refraction. To do this,
one must have an idea of how much deviation in the index can be attributed to random
variations. One way to assess this is to find an average value for the index, and from that to
determine a standard deviation. The average and standard deviation can be obtained from
the Analyze/Statistics menu item in Ga3. You will need to draw a box around your data
points before the Statistics will be active. Note the result in your Data. Use the std. dev.
(sn ) to find the standard error or the deviation of the mean using
sn
sn̄ = √ .
N
N is the number of values averaged (probably 5. . . ).
refraction as n = n̄ ± sn̄ .
4.3.1
(4.4)
Specify your measured index of
Part 3: Total Internal Reflection
In this experiment you will also use the Light
Ray Box shown in Figure 4.1. One option
is to print the template in Figure 4.5 and
to use it instead of constructing everything
on a blank page. Draw a long line for the
slanted surface and another at 90◦ for the
surface normal. Position the slanted end of
the Lucite block along the surface line. Slide
the paper to arrange the ray to enter the
Lucite block at the squared off end of the
block. This is the end opposite the slanted Figure 4.3: A sketch illustrating internal
end. Have the ray cross through the block reflection at the surface of a Lucite block. We
and exit the slanted side. Observe the ray can see and note where the ray enters the block,
that exits this side as you turn the paper and where the ray hits the surface, and where the
block to vary the angle that the ray strikes reflected ray exits the block.
the inside surface of the slanted side; this is the incident angle θ1 . You should also observe
that there is a significant amount of intensity in the ray reflected off the inside surface.
Record your observations in your Data. As you increase the incident angle the angle of
refraction, θ2 , will also increase. Since θ2 will always be larger than θ1 , there will come an
angle of θ1 for which θ2 should equal the maximum of 90◦ . At all angles of incidence larger
than this critical angle, total reflection occurs and you should observe a noticeable increase
in the intensity of the reflected ray. Total internal reflections are the most efficient optical
reflections. Record your observations in your Data.
Adjust the block so that the refracted ray just skims the slanted surface of the block
and the incident ray hits the surface at the surface normal line. Note any observations of
interest as you do this operation. Decide on what position best represents the critical angle
44
CHAPTER 4: EXPERIMENT 2
for the incident ray. Now mark the point where the incident ray enters the block and where
the reflected ray emerges. If the block moves on the paper, reposition it on the surface line
before marking the rays. Now, remove the block, use the points (and the point of incidence)
to recreate the incident and reflected rays as they appeared inside the block. Measure the
angle of incidence. Check this with the angle of reflection since they are equal. Be sure to
record your units and to estimate your measurement errors. Consider all of the steps needed
to construct the rays and to measure the angles. Use this critical angle to calculate the index
of refraction for the Lucite block,
n=
1
nair
≈
,
sin θc
sin θc
and compare with the value you got in part one. Does it agree within the uncertainty
of the first measurement as determined from the standard error? Might the error in your
measurement of critical angle be large enough to explain any disagreement? Comment on
this in your Analysis.
Checkpoint
If two adjacent media have the same index of refraction, n, can you observe the
phenomena of reflection or refraction?
Checkpoint
What is a critical angle? What are the two conditions that allow total internal
reflection to take place?
4.3.2
Part 4: Optical Fiber
One of the more recent and ubiquitous applications of total internal reflection is the optical
fiber. Fiber optics has revolutionized the communications industry. A fiber consists of a
long thin thread of glass called the core surrounded by an outer shell of a material with a
lower index of refraction called the cladding. Light entering the end of the core of an optical
fiber is transmitted or piped to the other end with very little loss in intensity even though
the fiber may be bent in a circular shape. The thinness of the fiber and the lower index
of refraction in the cladding ensures that light will always strike the fiber side at an angle
greater than the critical angle for total internal reflection and be totally reflected back into
the fiber. Thus the light bounces off the inside as it caroms down the length of the fiber
following every bend or twist.
Find the optical fiber among the items on your lab table. Be careful in handling the
fiber. It is, after all, a piece of glass and will break if bent too sharply. Align one end of the
45
CHAPTER 4: EXPERIMENT 2
fiber with the ray emerging from the ray box. Observe the light emerging from the other end
of the fiber. It will look like a bright pinpoint of light. Point this end of the fiber vertically
down onto a sheet of paper on the table with the end of the fiber held about five millimeters
above the table. You should see a bright spot on the paper where the light rays coming from
the fiber hit the paper. The light has been channeled through the fiber even around the
bends as the ray bounces off the inside surface of the fiber, possibly many times. The light
persists with little loss of intensity because of the great efficiency of these reflections that are
at such steep angles to the surface normal as to always be in the realm of total reflection.
Now, carefully rotate the incident end of the fiber to introduce and angle between the
incident ray and the fiber end’s normal. Observe that the spot on the paper has expanded
to form a ring of light. Note these observations and try to explain them in your Data.
Checkpoint
In the case of fiber optics do you expect the core or the cladding to have a greater
value for the index of refraction? Why are optical fibers immune to electrical noise?
4.4
Analysis
Which is larger between your ability to construct the light rays on paper and to measure the
angles and the difference between your incident and reflected angles? Between the accepted
index of refraction (1.495) of Lucite and those measured in Part 2 and/or Part 3? Between
the two measurements of Lucite’s index of refraction from Part 2 vs. Part 3? This last
question suggests the self-consistency among your measurements.
How accurately have you constructed and measured your ray diagrams? What other
sources of error have you noticed and how has each affected your data? Might these errors
be large enough to explain your differences?
4.5
Conclusions
What physical relations do your data support? Contradict? Which are not satisfactorily
tested? Communicate with complete sentences and define all symbols.
What have you measured that you might need to use in the future?
46
1
2
3
4
5
O
3
3
3
CHAPTER 4: EXPERIMENT 2
Figure 4.4: A template to aid the several measurements of index of refraction.
47
2
2
O
1
1
CHAPTER 4: EXPERIMENT 2
Figure 4.5: A template to aid the observation of total internal reflection and the critical
angle.
48
Chapter 5
Experiment 3:
Geometric Optics
5.1
Introduction
In this and the previous lab the light is viewed as a ray. A ray is a line that has an
origin, but does not have an end. Light is an electromagnetic disturbance, and as such is
described using Maxwell’s equations, which expresses the relationship between the electric
and magnetic fields in an oscillating wave.
Light propagates as a wave, yet many optical phenomena can be explained by describing
light in terms of rays, which in the model for light travel in straight lines in a homogeneous
medium. This model is referred to as Geometric Optics and is a very elementary theory. In
this theory, light travels from its origin at a source in a straight line, unless it encounters
a boundary to the medium. Beyond this boundary may be another medium which is
distinguished by having a speed of light different from the original medium. In addition,
light may be reflected at the boundary back into the original medium. A light ray that
returns to the original medium is said to be “reflected”. A ray that passes into another
medium is said to be “refracted”. In most cases, light passing across a boundary between
two media is partly reflected and partly refracted. In this lab we will observe how the laws
governing reflection and refraction, which were explored in the previous lab, can be applied
to explain how images are formed by mirrors and lenses.
Any mirror or lens can be referred to as an optical element. Imaging refers to the
process by which a single optical element or a set of optical elements produce an image or
reproduction of the light coming from an object. We perceive an object by observing light
coming from the object. We are accustom to the fact that light diverges from an object and
travels in a straight line from the object. Our two eyes and our sense of perception use these
facts to locate objects in our environment and to create a mental picture of our surroundings.
An optical element can redirect diverging light rays so that they appear to diverge from
a different source. Thus an image is formed apart from the original object. The image can
have one of two possible natures. If the light is merely redirected to appear to diverge from
a different location, and thus the light in fact was not focused at that point, it is said to be a
49
CHAPTER 5: EXPERIMENT 3
virtual image. The light’s source point is not in a virtual image, but the rays’ new directions
make it seem like they came from the virtual image. The most common example would be
the reflection in a plane mirror. The image would appear to be behind the mirror surface,
and yet behind the mirror may be a brick wall, hardly conducive to propagation of light. On
the other hand, light may be redirected to converge at a point, after which it would diverge
from that point in a similar manner to the way it originally diverged from the object. The
resulting image is said to be a real image when light actually diverges from the location of
the image. A screen or white paper placed at a real image plane will show a duplicate of the
object. Perhaps it is obvious that a screen behind a mirror will show no such duplicate.
The principle objective of geometric optics is to be able to determine the location of an
image for certain optical elements arranged in a specific geometry. This may be accomplished
in two ways. One can sketch key ray paths in a scale drawing of the geometry or one can
calculate the image distance and properties using a set of equations.
The Plane Mirror
The mirror is the simplest of optical
elements to understand. Everyone is familiar with the imaging properties of a plane
mirror. If you stand in front of a plane
mirror you see your image behind the mirror.
The location of the image of an object placed
in front of a mirror can be diagrammed
knowing that the surface of the mirror reflects light with an angle of reflection equal
to the incident angle.
Let us look briefly at the properties of
the image formed by a plane mirror. It is
formed behind the mirror, it is right side up
with respect to the object, and it is the same
size.
seem to
come from
here
ho
rays
extrapolated
rays
normal
do
Object
hi
5.1.1
di
Mirror
Image
Figure 5.1: Light rays reflected by a plane
mirror are illustrated. It looks as if the rays
originated behind the mirror from a virtual
image.
General Information
Note: For the image left is right and right is left. The image seems to be left - right
inverted, but this is a separate issue.
By convention we measure the object distance do as a positive value when in front of the
mirror and image distance di when behind the mirror as negative. Hence for the case of a
50
CHAPTER 5: EXPERIMENT 3
plane mirror where the image is behind the mirror as far as the object is in front then
di = −do
(5.1)
The relative size of the image compared to the object is the magnification, M , defined by
the relation
hi
M= .
(5.2)
ho
For a plane mirror the magnification is M = +1. We emphasize the positive sign because
the sign of M has a significance we will only appreciate later. It tells us if the image is
right-side-up (upright) or upside-down (inverted) relative to the object. Figure 5.1 shows a
diagram locating the image of a plane mirror. In the case of a plane mirror where the image
is oriented the same as the object, M is positive. Even more interesting is the fact that the
magnification is directly related to the relative distances between the object or image and
the mirror. In general M can be calculated from
M =−
di
.
do
(5.3)
Using the relation in Equation (5.1) we get M = +1 again. Such will not always be the case
for mirrors in general, but seem to be true for plane mirrors.
We note finally that the rays of light form an observable image because they appear to
diverge from a point other than where the object is located. Since our eyes observe diverging
rays, we can see the image. For a plane mirror this point is behind the mirror and we can
see the image. In fact, the rays cannot actually be traced back to that point; if we try, we
get stopped by the mirror. They never really pass through the point of apparent divergence.
That point may very well lie inside a solid wall or behind the wall in another room. We refer
to the image as a virtual. Not all images are virtual. But all virtual images are erect and
have negative image distances in the case of a single mirror.
Checkpoint
What does the relative size of object and image depend on?
5.1.2
The Concave Mirror
A mirror surface can be fabricated as part of a spherical surface of radius R. By convention
a positive radius is one that is measured to the left of the surface assuming light to be
approaching from the left to be reflected off the surface. In fact, all distances are positive on
the side where light is bouncing around. The reflecting surface would be termed a concave
mirror when R > 0. The principle axis is a line that strikes the mirror in the center at
normal incidence. Any light ray that is parallel to this axis when it is reflected off the mirror
will arrive at the same point along the principle axis. This is called the focal point and it
51
CHAPTER 5: EXPERIMENT 3
can be shown that this point lies a distance f from the mirror where f = R/2. These acts
provide the circumstances for drawing two rays (1 and 2) diverging from the tip of the object
that will re-converge at a specific point to locate the image position for a particular object
location. We show how these rays can be used to locate an object in Figure 5.2. A more
useful interactive diagram called an applet can be found on the internet at
http://groups.physics.northwestern.edu/vpl/optics/mirrors.html
do
1
ho
4
2
R
f
3
hi
Object
di
Image
Mirror
Figure 5.2: Light rays reflected from a concave mirror are illustrated. Four rays are easy
to draw for mirrors: Incident parallel to the axis passes through the focus after reflection,
incident through the focus reflects parallel to the axis, incident through the sphere’s center
reflects through the center, hits the mirror on the axis reflects at the same angle. The
diverging rays are focused at a real image point.
The applet makes use of a third ray which, if it strikes the mirror normal to the surface
at zero incidence angle, is reflected back on itself. A fourth ray can be obtained where the
ray strikes the mirror at the vertex, where the principle axis meets the mirror surface. Such
a ray is reflected at an angle equal to the angle between the ray and the principle axis.
The most obvious thing about the image formed by this configuration is that the image
is inverted. It also appears in front of the mirror. Such an image is so foreign to us that you
really have to see it to appreciate it. Take a common metal spoon and hold it at arms length
with the concave portion facing you. When you look into the spoon you should see your
reflection and everything else behind you in the room inverted. It is harder to discern that
the images are in front of the mirror; never-the-less, it is the case. By convention we say that
an image located in front of the mirror has a positive image distance. From the definition
of magnification in Equation (5.3), M must be negative if both do and di are positive. This
agrees with the fact that the image is inverted.
52
CHAPTER 5: EXPERIMENT 3
The image in Figure 5.2 can be located analytically using the expression
2
1
1
1
= =
+ .
R
f
do di
(5.4)
The image is reduced in size. This further bears out the relation in Equation (5.3) that
ties the magnification to the object and image distances. Here the image lies closer to the
mirror than the object and hence is smaller. We also note that the rays of light actually pass
through the image location and re-diverge. By convention we say that this image is a real
image. Visibly it looks like an object is really located at that point, and the phenomenon is
the source of many magic tricks and optical illusions. The fact that the image is inverted
and located at a positive image distance goes along with the real nature of the image. A real
image will be formed if the object is located anywhere between infinity and the focus of the
mirror. Real image can be projected. That is, if you were to place a white card or projection
screen at the point where the image is formed, the image will appear in good focus on the
screen.
-di
1
do
hi
3
Object
ho
2
4
Image
f
R
Mirror
Figure 5.3: Light rays emitted from a very close-up object are reflected by a concave mirror.
In this case the rays do not focus; however, they appear to come from a virtual image behind
the mirror. Our eyes can then focus these diverging rays and see the virtual image behind
the mirror despite its absence. See the caption of Figure 5.2 to learn how to draw these four
easy rays.
If the object is moved to a point closer than the focus of the mirror the rays will no longer
re-converge to form a real image. Instead the rays appear to diverge from a point behind
the mirror as shown in Figure 5.3. Such an application would be when you use a makeup
mirror. Note that the virtual image is enlarged and right-side-up. Virtual images are not
projectable, since the rays never come to a focus at any real point in space.
53
CHAPTER 5: EXPERIMENT 3
5.1.3
Convex Mirror
A convex mirror (R < 0) is often called a divergent mirror. Light rays parallel to the
principle axis are reflected away such that they appear to diverge from a focus behind the
mirror. An image distance marked off behind the mirror is considered negative and locates a
virtual image. In a similar manner according to the convention, a focus behind the mirror is
negative, and virtual. Indeed, the rays never do pass through this focus just like rays never
pass through a virtual image.
The images formed by a convex mirror are virtual regardless of where the object is placed
in front of the mirror. Figure 5.4 shows the ray diagram locating the image. Note that ray 1
appears to diverge from the virtual focus, and ray 2 appears to be headed for the virtual
focus though neither ray reaches this focus. Note also that both the radius and the focus
would have numerical values with a negative sign.
Checkpoint
What is the difference between a real and a virtual focus?
Checkpoint
What is the difference between a real and a virtual image?
5.1.4
Lenses
Not everyone has personal experience using lenses, or so it might seem. Besides the most
common application in eyeglasses used to correct imaging problems, campers, for example,
have been know to use a focusing lens to start a campfire without matches using the sun’s
energy. It gets more personal than that, however. Each of us uses a natural imaging system
in our eye to see, which in part relies on a lens within each eye.
The surface of a piece of glass can act as an optical element that changes the direction
of a light ray as it passes through the surface. We explored Snell’s Law that describes this
phenomenon in the last lab. In most applications of an air-glass surface the piece of glass
is thin and the rays quickly encounter the opposite side of the glass at a glass-air boundary
where the light emerges from the glass. There are many applications where only this one
interface is considered such as looking at objects underwater. The cornea of the eye is an
example of such a surface. We will not deal with this imaging process, but consider only
applications where the light emerges from the optical element into air again. Such problems
are referred to as thin lens applications.
A plane piece of glass with parallel surfaces usually results in a slight sideways displacement of the original beam but no noticeable angular deflection. A pane of glass is transparent
54
CHAPTER 5: EXPERIMENT 3
do
1
ho
3
4
2
Object
hi
di
f
R
Image
Mirror
Figure 5.4: Light rays reflected from a convex mirror appear to come from a virtual image
behind the mirror.
and transmits rays from an object undistorted. Such a simple case is worth a quick look
compared to its reflection analog the case of a plane mirror. When looking at an object
through a pane of glass we are in fact looking at the image of the object which is located at
nearly exactly the same spot as the object itself. We have two choices. We can rewrite the
imaging equations (5.1), (5.2), (5.3) and (5.4) to include the fact that the image is now on the
same side of the optical element as the object, or we can change the convention to say that
a virtual image is formed on the opposite side of the optical element from the observer. The
accepted convention is to choose the latter. The accepted convention is that a real object
(+do ) is on the side where light enters the lens, but a real image (+di ), a real radius (+R),
and a real focus (+f ) are on the side where light exits the lens. We will see the ramifications
of this in the images formed by a thin lens. We should also mention that lenses have two
foci; each is a distance |f | from the lens’ center where one is on each side of the lens and
both are on the optical axis. Convergent lenses have positive foci and divergent lenses have
negative foci.
5.1.5
Convergent Lens
A convergent lens redirects parallel rays such that they come to a focus. It is the lens analog
to the concave mirror. An example of a convergent lens is one with two convex surfaces
although other combinations of surface curvatures can also form a convergent lens.
As we did for mirrors, we define the principle axis to be a line that strikes the lens in
55
CHAPTER 5: EXPERIMENT 3
Figure 5.5: Light rays passing through a convergent lens focus at a point behind the lens.
Lenses have three rays that are easy to draw: Rays parallel to the axis are focused through
the second focal point, rays passing through the first focal point are transmitted parallel to
the optical axis, and rays passing through the lens’ center are undeflected.
the center at normal incidence. Any light ray that is parallel to this axis before it passes
through the lens will be redirected to pass through a single point. This is called the focal
point and it can be shown that this point lies a distance f from the lens’ center. Unlike the
mirror the radius of the surface of the lens is not easily related to the focus; never-the-less,
all rays diverging from a point on the object will re-converge at another specific image point
after passing through the lens. One of these rays (1) is emitted parallel to the principle axis
and is bent to pass through the positive focus on the far side of the lens.
Because a thin lens has two operational sides, (it can be turned around and work just
as well), it has a second focus on the same side as the object. Another ray passing through
this focus (2) is redirected to be parallel to the optical axis.
We show how these rays can be used to locate an object in Figure 5.5. A more useful
interactive diagram called an applet can be found on the internet at
http://groups.physics.northwestern.edu/vpl/optics/lenses.html
The applet makes use of a third ray that strikes the lens at the vertex, where the principle
axis meets the lens surface. Such a ray (3) passes through the lens undeflected.
The most obvious thing about the image formed by this configuration is that the image is
inverted just as with the concave mirror. Contrary to the mirror analog, the image appears
behind the lens. Such an image is so foreign to us that we really have to see it to appreciate
it. Such a convergent lens is not as readily available as a mirror. If you have access to a
magnifying glass you can demonstrate the real image formed by such a lens. By convention
we say that an image located after the lens has a positive image distance.
56
CHAPTER 5: EXPERIMENT 3
Checkpoint
What is a lens?
General Information
Note the simple change in convention from mirrors. From the definition of magnification in Equation (5.3), M must be negative if both do and di are positive. This agrees
with the fact that the image is inverted.
Checkpoint
What is the principle axis of a mirror and of a lens?
Figure 5.6: Light rays emitted from a very close object do not focus; however, they appear
to come from a virtual image instead of the object. The ray directed away from the first focus
is transmitted parallel to the axis, the ray incident parallel to the axis is transmitted through
the second focus, and rays passing through the lens’ center are undeflected. For do < f , these
rays diverge less than before.
The image in Figure 5.6 can be located analytically using the same expression we used
for mirrors,
1
1
1
=
+ ,
(5.5)
f
do di
57
CHAPTER 5: EXPERIMENT 3
but the focal length is more difficult to compute for a lens.
The image is reduced in size. This further bears out the relation in Equation (5.3) that
ties the magnification to the object and image distances. Here the image lies closer to the
lens than the object and hence is smaller. We also note that the rays of light actually pass
through the image location and re-diverge. By convention we say that this image is a real
image. Visibly it looks like an object is really located at that point, and a plane card placed
at that point will display the image projected on it. Real images are projectable for lenses
as well as for mirrors. This phenomenon is applied to camera imaging as well as to how our
eyes work. The fact that the image is inverted and located at a positive image distance goes
along with the real nature of the image. A real image will be formed from a convergent lens
if the object is located anywhere between infinity and the focus of the lens.
If the object is moved to a point closer than the focus of the lens, the rays will no longer
re-converge to form a real image. Instead the rays appear to diverge from a point in front of
the lens as shown in Figure 5.6. Such an application would be when you use a magnifying
glass. Note that the virtual image is enlarged and right-side-up. Virtual images are not
projectable, since the rays never come to a focus at a real point in space, but the resulting
diverging rays can be focused by our eyes.
5.1.6
Divergent lenses
Lens
do
1
3
hi
ho
2
Object
-di
-f
-f
Image
Figure 5.7: Light rays passing through a divergent lens appear to come from a virtual image
instead of the object itself. Three easy rays for a divergent lens are parallel rays are deflected
away from the axis and appear to come from the first focus, rays heading toward the second
focus are deflected parallel to the optical axis, and rays passing through the lens’ center are
undeflected.
A divergent lens is the analog of a convex mirror. Light rays parallel to the principle axis
get redirected away from the optical axis such that they appear to have originated from the
same point. An image distance marked off in front of the lens is considered negative and
58
CHAPTER 5: EXPERIMENT 3
locates a virtual image. In a similar manner according to the convention, a focus in front of
the lens is negative, and virtual. Indeed, the rays never do pass through this focus just like
rays never pass through a virtual image. This focus is not to be confused with the real focus
of a convergent lens.
The images formed by a divergent lens are virtual regardless of where the object is placed
in front to the lens. Figure 5.7 shows the ray diagram locating the image. Note that ray 1
appears to diverge from the first virtual focus, and ray 2 appears to be headed for the
second focus though neither ray reaches its focus. Note also that the virtual focal distances
are negative.
Checkpoint
What is the difference in the convention for mirrors and the convention for lenses?
5.1.7
Part 1: Mirrors
Set up the ray box used in the last experiment but use the 5-slit mask. The ray box may
have to be adjusted to make the rays parallel; use at least two meters for this adjustment.
The piece of the box holding the slits will slide in the piece holding the light and allow you
to cause the rays to emerge parallel to each other. Always be sure the rays are parallel while
you are measuring the focus of optical elements. Locate the mirror block. It is roughly a
triangular silver plastic piece. One side is flat, one side is concave, and one side is convex.
With the flat side placed in the beam of parallel rays observe how the rays are redirected
while maintaining the parallel structure. Note too that the deflection angle is twice the
incident angle. A small turn of the block results in twice as much change in the direction of
the rays. Briefly note your observations in your Data.
With the concave side placed in the beam, observe how the rays are redirected to a focal
point and from there re-diverge. It might help to elevate the front or the back of the ray
box by placing the ruler and/or the protractor under it. With the convex mirror facing the
beam the rays diverge and appear to emanate from a focus behind the surface.
Place the concave mirror so that the center ray hits the center of the mirror and rotate
the mirror until the focused rays are on the optical axis; they intersect the center ray at the
same point. Carefully mark the mirror surface with a pen or pencil on the record paper. If
the mark is not exactly below the mirror, move the mirror exactly to the mark and verify
that the rays still converge on the optical axis. Mark the point where the rays converge and
circle the area where one might reasonably choose an alternate focus. It might help to block
the center ray at the ray box temporarily. Remove the mirror and paper, turn on your lamp,
and carefully measure the mirror’s focal length. The radius of the circle around the focus is a
reasonable estimate of the error in this measurement. Record your focal point measurement,
units, and error in your Data.
59
CHAPTER 5: EXPERIMENT 3
Place the convex mirror so that the center ray hits the center of the mirror and is
retroreflected back into the center slit. Carefully mark the mirror surface with a pen or
pencil on the record paper. If the mark is not exactly below the mirror, move the mirror
exactly to the mark and verify that the center ray still reflects along the optical axis. Mark
two points on each incident ray and each reflected ray; separate each pair of points by as
much distance as possible to make reproducing the rays’ angles more reliable. Remove the
mirror and paper, turn on your lamp, and carefully reconstruct the five incident and the five
reflected rays. Extend all rays to the mirror’s surface. Each incident ray should intersect its
reflected ray at the mirror’s surface; if this is not the case, use your records on the paper
to reconstruct the experiment with the ray box. This will allow you to adjust your record
points to agree better with the rays so that they intersect at the mirror as they should.
Extend all five reflected rays through the mirror’s surface and a few cm further than they
converge at a virtual focus. Mark the point where the rays appear to originate and circle
the area that one might reasonably choose as an alternate focus. Use the ruler to measure
the mirror’s (negative) focal length. The radius of the circle around the focus is a reasonable
estimate of the error in this measurement. Record your focal point measurement, units, and
error in your Data.
5.1.8
Part 2: Lenses
Set up the ray box used last week but use the 5-slit mask. The ray box may have to be
adjusted to make the rays parallel; use at least two meters for this adjustment. The piece
of the box holding the slits will slide in the piece holding the light and allow you to cause
the rays to emerge parallel to each other. Always be sure the rays are parallel while you are
measuring the focus of optical elements. Locate the two-dimensional convergent lens (convex
surfaces). Place this lens in the beam of parallel rays and observe how the rays converge to
a focus on the side of the lens away from the source. Move the lens around and note how
the emerging rays respond to the various lens positions. Place the lens perpendicular to the
rays such that the center ray hits the lens center. This placement should cause the rays to
converge on the optical axis (where the center ray would be without the lens). If this is not
the case, adjust the lens position to make this true. Mark both lens surfaces (or the center
of both sides) so that the lens center can be located later. Mark the point where the rays
converge and circle the area one might reasonably choose an alternate focus.
Remove the lens and paper and turn on your lamp. Use your ruler to reconstruct the
center ray; extend this ray back past the lens location. Use your ruler to locate the center of
the lens. Carefully measure the distance between the lens center and the focus. The radius
of the circle of alternate foci is a reasonable estimate for the error in this measurement.
Record your measured focus, its error, and its units in your Data: fc.l. = (f ± δf ) U.
Locate the two-dimensional divergent lens (concave surfaces).
60
CHAPTER 5: EXPERIMENT 3
WARNING
Be careful not to drop this lens because its thin center makes it easy to break.
Be sure the rays from the ray box are parallel. Place the lens in the beam of parallel
rays and observe how the rays appear to diverge from a point in front of the lens. Move the
lens around and note how the diffracted rays respond to the various lens positions. Place
the lens perpendicular to the rays such that the center ray hits the center of the lens. When
this is true, the center ray should remain on the optical axis. Mark both surfaces of the
lens (or the center of both edges) so that the lens center can be located later. Mark two
points on each diffracted ray so that each ray can be reconstructed later. Remove the lens
and paper and turn on your lamp. Use your ruler to reconstruct the center ray; extend this
ray back past the apparent point of origin for the five rays. Use your ruler to locate the
center of the lens. Use your ruler to reconstruct all five rays and extend each ray past the
lens and a few cm past the optical axis. The extended rays should converge to a point; if
not, use your record paper to reconstruct your experiment and to determine how to adjust
your points for better agreement. Mark the point of convergence and draw a circle around
the area one might reasonably choose an alternate focus. Carefully measure the (negative)
distance between the lens center and the virtual focus. The radius of the circle of alternate
foci is a reasonable estimate for the error in this measurement. Record your measured focus,
its error, and its units in your Data: fd.l. = (f ± δf ) U.
5.1.9
Part 3: A Lens System
Place the convergent lens in the beam and form a focused beam. Adjust the lens position to
optimize the focus. Use the focus as an “object”. Place the divergent lens in the path of the
diverging rays at least 6 cm after the focus and observe that the rays are redirected by the
lens so that they appear to be diverging from a different point. See position 1 in Figure 5.8.
The lens should be perpendicular to the optical axis and the center ray should hit the center
of the lens. The center ray will remain on the optical axis when this is true. The virtual
image is where the new rays seem to come from. Mark both divergent lens surfaces (or the
center of both edges) so that the lens’ center can be located later. Mark the location of the
“object” and draw a circle around the area that might alternately be chosen as the focus (i.e.
the “object”). Mark two widely separated points on each diffracted ray after the divergent
lens. Remove the lens and paper and turn on your lamp. Reconstruct the center ray and
extend it back to the “object”. Use the ruler to locate the lens center. Reconstruct the five
diffracted rays and extend each back a few cm past where they cross the optical axis. All
five should intersect the optical axis at the same point. If this is not the case, use your
record paper to reconstruct your experiment and to adjust your points for better agreement.
Measure the (negative) virtual image distance between the lens center and the virtual image.
The radius of the circle of alternate radii is a reasonable estimate of the measurement error.
Record your measurement, its error, and its units in your Data. Repeat for your “object”
distance and calculate the divergent lens’ focal length using Equation (5.5). Does this focus
61
CHAPTER 5: EXPERIMENT 3
agree with the focus measured directly? We will check this numerically in our Analysis.
Since your object distance and image distance each have error, it should be obvious that
your calculated focal length also has error due to both of these sources. Calculate the error
in your focal length using
v
δf = f
u
u
2t
δdo
d2o
!2
δdi
+
d2i
!2
(5.6)
.
do
-di
Object
Virtual
Image
(a)
Virtual
Object
Image
-do
di
(b)
Figure 5.8: An illustration of two strategies for measuring the focal length of a divergent
lens. In (a) the rays that diverge from the first lens’ focus are spread even further by the
concave lens. In (b) the rays that would have converged at one focus are redirected to a
different focus.
Now place the divergent lens at position 2 in Figure 5.8, between the convergent lens
and the focal point and at least 5 cm from the focal point. Observe that the rays converge
to a new focal point a little further away from the lenses. This is a real image. But where
is the object? The original focus has disappeared when the lens was placed in the beam.
It has become a virtual object! Remove the divergent lens and mark the location of the
original focus; draw a circle around the area of alternate possible foci. Place the lens in the
beam perpendicular to the optical axis such that the center ray hits the lens center. The
center ray should remain on the optical axis when this is true. Mark the image location
(the new focus point), the area of possible alternate foci, and the divergent lens location.
Locate the lens center and measure the object and image distances; be sure to assign the
correct signs. Record these measurements, their errors, and their units in your Data. Again
use Equation (5.5) to calculate the focus of the lens and use Equation (5.6) to estimate its
error. Don’t forget to record this measurement, its units, and its error in your Data. How
well does it match the previous two measurements?
62
CHAPTER 5: EXPERIMENT 3
Checkpoint
What is a virtual object?
5.1.10
Part 4: Lenses
Measure the focus of a real lens. Using a
source far away (several meters) find the
point where the image of this distant source
is brought to a focus on a screen. With the
room lights dimmed use the light coming
through the lab door or window as an object. How does this compare with the value
printed on the lens housing? Keep in mind
that your measurement might not be very
accurate.
Place the optical source at one end of the
optical bench and place the white screen on
the opposite end of the optical bench. Place Figure 5.9: A good way to measure the focal
a convergent lens between the source and the length of a thin lens. There will be two lens
screen but nearer to the source and find the positions that focus the object’s image on the
spot where the image of the source projected screen. Note these positions so that you can
onto the screen is in focus. Observe that the find the distance, d, between them.
image is larger than the source because the
image distance is larger than the source distance to the lens. How far can you move the
lens before the image is noticeably out of focus. Use this distance as an estimate of your
measurement error.
Record the lens location, its error, and its units: l1 = (x ± δx) U. Calculate the object
distance do and the image distance di and use Equation (5.5) to find the focal length of the
lens. Is it comparable to the value observed above using the open door?
Now we will measure the focus in another way. There are two possible locations where
a focused image can be achieved. Move the lens closer to the screen until a second smaller
focused image appears on the screen. What has changed? Note the position of the lens for
this geometry. How far can you move the lens before the image is noticeably out of focus?
What does this distance mean? Record this lens location: l2 = (x ± δx) U. Calculate the
object distance do and the image distance di and use Equation (5.5) to find the focal length
of the lens.
Calculate the distance, d = |l2 − l1 |, between the positions of the lens for which the image
was in focus as shown in Figure 5.9. Estimate the error in this distance using the errors in
the two lens positions,
q
δd = (δl1 )2 + (δl2 )2 .
63
CHAPTER 5: EXPERIMENT 3
This distance can be used as another way to measure the focal length of the lens. Measure
the total distance D between the object and the screen. Estimate the error in this distance
δD. The focal length of the lens is calculated using
f=
D 2 − d2
.
4D
The errors in this calculated measurement is due to the errors in d and D. Use the errors
δd and δD
v
!2
!2
u
u d
d
D 2 + d2
t
δf =
δd +
δd .
δD ≈
2
2D
4D
2D
to estimate the error in f .
5.2
Analysis
We have measured three different values for the focal length of the diverging cylindrical lens.
Label them such that f1 < f2 < f3 and compare f1 to f2 and f2 to f3 using Difference,
∆i = fi − f2 , i = {1, 3}.
Note that this “NULL hypothesis” was computed using two numbers that have experimental
error. This means that ∆ also has error given by
σi =
q
(δf2 )2 + (δfi )2 , i = {1, 3}.
(5.7)
If f1 = f2 , then ∆ = 0 or NULL; however, the results of measurement almost never turn
out to be the same so the natural question becomes, “How nonzero must ∆ be before the
difference is significant?” Use Equation (5.7) to convert the units of ∆ from cm to σ. Is
∆ < σ? Is ∆ < 2σ? Is ∆ > 3σ?
We have also measured three different values for the focal length of the real lens on
the optical bench. Repeat the analysis above for these three values. For each of these
four experiments, determine whether the focal lengths are statistically distinct. One sigma
disagreements happen about 1:3 even when the two numbers are the same just because
random things happen to measured data. Two sigma disagreements happen about 1:22; even
these chances are too large for us to decide that our hypothesis is definitely false. Three
sigma disagreements happen only about 1:370, so differences this large lead us to admit that
the two numbers that we wound up comparing are probably not the same. Larger differences
are yet less likely. Statistics can tell us that the two numbers are probably not equal, but
statistics cannot tell us why. Perhaps we have underestimated one or more of our errors.
Perhaps the devices in our experiments have properties that contribute to our data and of
which we have not properly compensated. Perhaps the environment in which we performed
our experiment has contributed to our data. Perhaps our hypothesis is, in fact, false. As
experimenters, we must evaluate all possibilities and decide which is the truth. Enumerate
64
CHAPTER 5: EXPERIMENT 3
some of these other sources of error and estimate how each affects your data. In your view is
it more likely that we have underestimated how these other effects affected our data or that
the theory we tested is false? Keep in mind that others have investigated these theories also
and that their results are in the literature.
5.3
Conclusions
What physics do your data support? What do they contradict? What did you test and fail
to resolve? Do your data support Equation (5.5)? Might Equation (5.3) be true? We did not
test Equation (5.3) numerically, but your observations on the optical bench might allow you
to address this qualitatively. Always define the symbols used in these equations; it should
not be necessary for your readers to read anything else to understand your Conclusions fully.
Are there any limitations on the focus equation? What can be used as objects? Did you
measure anything whose value might be useful later? The focal lengths of lenses and mirrors
might be useful information if we should use these optical elements again. Always include
measurement errors and units in these values.
65
CHAPTER 5: EXPERIMENT 3
66
Chapter 6
Experiment 4:
Wave Interference
WARNING
This experiment will employ Class III(a) lasers as a coherent, monochromatic light
source. The student must read and understand the laser safety instructions on
page 89 before attending this week’s laboratory.
Helpful Tip
Before beginning this experiment, it is probably a good idea to review the first several
pages of the Sound Experiment on page 25. Waves of all kinds are quite similar in
most respects so that the same interference between an incident and reflected sound
wave that caused standing waves in the sound tube leads to the effects that we will
observe today using light waves.
6.1
Introduction
In this and the following lab the wavelike nature of light is explored. We have learned
that waves usually exhibit some periodic or oscillatory nature such as the water level at a
particular point on a pond steadily rising and falling as waves pass. For light (electromagnetic
radiation) it is the electric and magnetic fields which oscillate in strength and direction. At
visible frequencies these oscillations occur so fast that they are exceedingly difficult to observe
directly (1014 Hz.)
Another important characteristic of waves is that they may interfere with each other.
In simple terms interference is the result of oscillating dips and rises adding together or
canceling out. A good example of interference is seen when the circular wave patterns from
two stones thrown into a pond meet. High points from the separate waves add to make even
67
CHAPTER 6: EXPERIMENT 4
T
T
1
2
t (T)
1
3
2
3
t (T)
(b)
(a)
T
Figure 6.1: In each illustration the top
two waveforms add point by point to yield
the bottom waveform. The resulting effect
can add as in the first case, cancel as in
the second case, or anywhere in between.
The difference between the three cases is
the amount of constant phase that has been
3
1
2
t (T)
added to the second waveform. This phase is
(c)
illustrated as a fraction of the total period.
Waves have exactly the same dependence on
position where the constant phase is in that case a fraction of wavelength instead of period.
higher points, dips from the two waves also add making lower dips, and when a dip from one
wave passes the same point as a high from the other they cancel.
Waves are partly characterized by surfaces of constant phase. If time is frozen, then the
argument of the wave’s function varies only in space and the function ωt = ϕ = k · r defines
a surface in space. In the specific case where ϕ = k · r = kx, x is constant but y and z
are arbitrary. Each x defines the function of a plane parallel to the y-z plane. This is a
plane wave. Alternately, ϕ = kr defines surfaces of constant radius or spheres centered at
r = 0. This is a spherical wave. Many other surfaces are possible, but these two are the most
important ones. Plane waves are by far the easiest to treat mathematically and spherical
waves are generated by point sources like atoms, molecules, and surface structures.
Checkpoint
What is a plane wave?
Figure 6.1 shows how two sinusoidal waves add together to produce a new wave. In this
lab we will see how interference affects the intensity pattern of light that has passed through
two narrow adjacent slits, many parallel slits (diffraction grating), and a special bulls-eye
pattern called a Fresnel zone plate.
68
d
CHAPTER 6: EXPERIMENT 4
Plane Wave
Figure 6.2: A plane wave incident upon two slits is transmitted as an interference pattern.
In the center of the pattern (m = 0), the distance L1 from the top slit to the screen equals the
distance L2 between the bottom slit and the screen. The time needed to transit this distance
is exactly the same for the two paths. The two waves are in phase as in Figure 6.1(a). As
we move down off the optical axis, L2 gets shorter and L1 gets longer until their difference is
half a wavelength and they cancel as in Figure 6.1(b). Further off axis the path difference is
a full wavelength and the peaks and valleys are aligned again (m = −1) as in Figure 6.1(a).
6.1.1
Part 1: Two Slit Interference Young’s Double Slit Experiment
Historical Aside
In 1801 Thomas Young devised a classic experiment for demonstrating the wave nature
of light similar to the one diagrammed in Figure 6.2.
By passing a wide plane wave through two slits he effectively created two separate sources
that could interfere with each other. (A plane wave is a wave consisting of parallel wavefronts all traveling in the same direction.) For a given direction, θ, the intensity observed
at point P on the screen will be a superposition of the light originating from every slit.
Whether the two waves add or cancel at a particular point on the screen depends upon the
relative phase between the waves at that point. (The phase of a wave is the stage it is at
along its periodic cycle; the argument of the sine or cosine function.) The relative phase
of the two waves at the screen varies in an oscillatory manner as a function of direction
causing periodic intensity minima and maxima called fringes (see Figure 6.2). The spacing
of the fringes depends on the distance between the two slits and the wavelength of the light.
If the width of the slits is narrow compared to a wavelength, the intensity of the two-slit
69
d
CHAPTER 6: EXPERIMENT 4
Figure 6.3: At an angle θ above the optical axis, the distance between the screen and the
bottom slit is longer than the distance between the screen and the top slit by δ = d sin θ as
shown by the geometry of the right triangle indicated.
interference pattern is given by
E(θ) = E0 cos β
and
I(θ) = I0 cos2 β ∝ |E(θ)|2
πd
β=
sin θ
λ
for
(6.1)
where θ is the angle between the initial direction, the location of the slits, and the observation.
d is the distance between the two slits, λ is the wavelength of the light, E is the electric field,
and I is the light intensity with units of energy per area per second.
Equation (6.1) is easily derived. The amplitude of the electromagnetic wave emanating
from either slit may be written as E = E0 sin(kx − ωt). After the wave emanating from
one of the slits travels a distance l the wave undergoes a phase shift ϕ = kl = 2πl
so that
λ
the electric field is of the form E = E0 sin(ωt + ϕ). The light arrives at the two slits at the
70
CHAPTER 6: EXPERIMENT 4
same time, so the phase difference is due to the difference in distances between the point of
observation, P, and the respective slit. This difference in distance is shown in Figure 6.3 as
a function of angle. It is seen that the wave front emanating from one slit lags behind the
other by ∆l = d sin θ. This gives a relative phase difference of
∆ϕ =
2πd
2π∆l
=
sin θ.
λ
λ
Since we are interested only in relative differences we can measure from the midpoint between
the slits and write the fields due to each slit as
1
E1 = E0 sin ωt + ∆ϕ
2
1
and E2 = E0 sin ωt − ∆ϕ .
2
Using the trigonometric identity, sin A + sin B = 2 sin 12 (A + B) cos 21 (A − B) gives
1
E = E1 + E2 = 2E0 sin ωt cos ∆ϕ = 2E0 cos β sin ωt.
2
(6.2)
When squared and averaged over time, this produces Equation (6.1). Maximum intensity
peaks occur at angles such that |cos β| = 1 and the difference between the two path lengths
is an integral multiple of wavelengths ∆l = d sin θ = mλ (see Figure 6.3). This translates to
β = mπ (m = ±1, ±2, . . .) and thus the angles of maximum intensity satisfy,
mλ = d sin θ and m = 0, ±1, ±2, . . .
(6.3)
If the width of the slits is greater than a wavelength the interference fringes are seen to
oscillate in brightness as seen in Figure 6.4. This is due to diffraction and will be studied in
a later experiment.
Checkpoint
Sketch two sinusoidal waves out of phase by 45◦ .
Checkpoint
Two waves in phase and each one with an amplitude A and intensity I meet at the
same point. What is the intensity of the signal observed at that point?
6.2
The Experiment
A helium-neon (HeNe) laser will be used to illuminate various patterned slides at normal
incidence. A two-meter stick and a ruler will be used to quantify the locations of the slides,
71
y
CHAPTER 6: EXPERIMENT 4
d
x
Plane Wave
Figure 6.4: The intensity profile of light transmitted through two actual slits. By changing
only the slit width a, we can verify that the intensity modulation indicated by the yellow trace
is due to the slit width a and NOT to the slit separation d. Presently, we are interested in the
closely-spaced, bright spots (the RED trace). The distance x between the slits and the screen
and the distance y between the optical axis and each spot can be measured with a meter stick
to determine θ using tan θ = xy .
the original beam path, and the observation points that have bright spots. This information
will be used to determine the angle θ needed to relate the laser’s wavelength to the distance
between two slits’ centers.
6.2.1
Part 1: Two-Slit Interference
You are provided a slide that has several sets of slits on it with separations and widths
as shown in Figure 6.5. You use the HeNe laser as your plane wave light source. The
experimental set up is as shown in Figure 6.6. If the laser beam is pointed onto a pair of
slits, an interference pattern similar to Figure 6.7 may be observed on a screen placed nearby.
The provided screen will hold masking tape where we may record the spot locations. This
allows the distance between fringes to be marked and measured easily and conveniently.
Observe the interference patterns. Draw what you see for each pattern on the slide in
your Data. Be sure also to note the slit dimensions for each pattern. How does the slit
separation affect the interference pattern? Can you detect any intensity variations in the
different fringes? Why does this occur? For each set of double slits identify the intensity
distribution caused by the width, a, of each slit as well as the interference fringes whose
spacing is related to the distance, d, between the two slits. Two of the double-slits in
Figure 6.5 are particularly interesting to observe because they have the same slit width, a,
72
CHAPTER 6: EXPERIMENT 4
but different slit separations, d. Consequently the minimum of the diffraction pattern must
occur at the same θ value but the spacing of the interference fringe pattern varies. Also, two
of the double-slits in Figure 6.5 have the same slit separation, d, but different slit widths, a.
This combination of four double-slit patterns allows you to isolate the effects of these two
independent parameters.
You will now make measurements using one
double-slit pattern. When the slit mask is perpendicular to the beam, its reflection will re-enter the laser.
Orient the screen perpendicular to the beam as well
and mark the locations of the interference fringes (the
finely spaced bright spots) on a strip of fresh tape.
Mark all visible spots; if fewer than five spots are
visible on each side of the beam axis, choose a different
double-slit pattern. Also measure the distance from
the double-slit slide to the screen, x, taking care not
to disturb the screen. Remove the double-slits and
circle the undeflected laser spot; this is the zero order
(m = 0) fringe. Take care not to tear your tape as you
remove it from the screen, make a table in your Data,
and measure the distances from the beam axis to the Figure 6.5: A photograph of Pasco’s
bright spots, ym . It will be more accurate to measure OS-8523 basic optics slit set. We are
2ym (the distance between the pair of dots on opposite interested in the double slits at the
sides of the beam axis) and then divide by two. Be bottom left.
sure to note your error estimates and units for these
measurements. Using λ = 632.8 nm as the wavelength of the laser-light and Equation (6.3),
calculate the slit separation. Do the distances, Rm , between the different bright spots and
the slits vary significantly more than the total of your measurement errors? If not then we
can make an approximation that
sin θm =
so that d =
mλ
sin θm
≈
ym
ym
≈
= tan θm
Rm
x
(6.4)
mλx
.
ym
You can download a suitable setup file for Ga3 from the lab’s website at
http://groups.physics.northwestern.edu/lab/interference.html
Otherwise, load one column in Vernier Software’s Graphical Analysis 3.4 (Ga3) program
with the order numbers (you can Data/Fill to do this quickly), load your measurements
of ym (or 2ym if this is what you measured) into another column, and create a calculated
column to hold your slit width results. Double-click the column headers to correct the labels
and to add the correct units. What will be the units of d? (If x and ym have the same
units, then these units will cancel in the ratio; otherwise, it will be more difficult for you
to determine the units of d.) Use the “Column” button to choose column “m” and column
“ym ” to enter the appropriate formula for d into the “Equation” edit control. (You will see
73
CHAPTER 6: EXPERIMENT 4
Figure 6.6: A sketch of our apparatus showing how the HeNe laser can be directed through
the slits and projected onto a view screen.
your column names instead of mine.) If you measured 2ym , you will need to divide this
column (the denominator) by two or to multiply the numerator by two. You will also need
to type in appropriate numbers for λ and x; Ga3 only works with numbers. You will also
need explicitly to tell Ga3 to multiply “*”.
y3
y-7
Figure 6.7: One example of an interference pattern due to HeNe laser light passing through
double slits. Large spots indicate large intensity. If the slit dimensions satisfy d = n a for
integer n, there will be missing orders at every nth spot as indicated by the black circles
containing no spot. The positions of the spots are measured as indicated for m = 3 on the
right and for m = −7 on the left. We MUST count the black circles despite the missing spot.
Calculate an average value for each double-slit separation and compare with those listed
in Figure 6.5. Plot the slit separation column on the y-axis and the order, m, on the x-axis.
Click on the smallest y-axis number and change the range beginning to 0. Do your values
of d vary more than you expect your errors to explain? If not, draw a box around your data
points with the mouse and Analyze/Statistics. Move the parameters box away from your
¯ is the best guess for your measurement of slit separation and
data points. The “mean”, d,
the “s. dev.” (or standard deviation, sd ) can be used to estimate the standard error or error
in the mean
sd
(6.5)
sd¯ = √ .
N
You can specify your slit separation using d = (d¯ ± s ¯) U.
d
6.2.2
Part 2: Diffraction Gratings
A system consisting of a large number of equally spaced, parallel slits is called a “grating”.
The diffraction pattern expected from a grating can be calculated in a way similar to the
74
CHAPTER 6: EXPERIMENT 4
Figure 6.8: Two Fresnel Zone Plates. Dark rings block light that would be out of phase
and would interfere destructively on the optical axis. Much smaller Fresnel Zone Plates can
focus X-rays without a lens. These are suitable for microwaves.
two slit system. A simple way to do this calculation is to represent the amplitude and phase
of each wave originating from one of the grating slits and impinging on a point on the screen
by a vector called a phasor (see textbook). Summing the phasors corresponding to each slit
gives the correct amplitude and phase of the total wave. The intensity distribution of the
light scattered off a grating with N very narrow slits is
sin N β
I(θ) = I(0)
N sin β
!2
(6.6)
where β is defined in Equation 6.3. This relation is very similar to the one for the interference
of two slits. In fact if N = 2, then substituting the identity sin 2β = 2 sin β cos β in the last
term of Equation 6.6) gives
sin N β
N sin β
!2
=
sin 2β
2 sin β
!2
=
2 sin β cos β
2 sin β
!2
= (cos β)2
and it is seen to reduce to the two slit formula Equation (6.2).
sin N β
The angular dependence of the interference maxima are described by the function N
.
sin β
With a large number of slits, this function has a numerator rapidly varying with θ and
a denominator slowly varying. As the number of illuminated slits increases, the intensity
peaks will narrow. The position of the fringe maxima generated by a grating is given by
Equation 6.3. Gratings are commonly used to measure the wavelength of light, λ. This may
be determined using Equation (6.6) and by measuring the angle between the maxima. These
measurements are called spectroscopy and will be very important in our last experiment.
Place the diffraction grating in the path of the green laser and perpendicular to the beam.
75
CHAPTER 6: EXPERIMENT 4
The number of slits per inch should be written on one side of the slide. Because the spacing
between slits is so small the angles of the maxima are quite large. You will need to keep
the screen close so that the 1st and 2nd order maxima can be seen. Measure the distance
between each of these spots and the central maximum. Don’t forget your units and error.
Also measure the distance between the screen and the grating slide. How much does the
intensity vary for the central, the 1st , and the 2nd order maxima?
For both measurements (or all four if you did not measure 2 ym ) made in step 2a) calculate
values of the wavelength of the light. Note that these angles are not small so that sin θ ≈ tan θ
does NOT apply to this case. You must use
ym
d
sin tan−1
.
λ=
m
x
(6.7)
Compare these values to the given wavelength of the laser, 532.0 nm. Since we used ym , x,
and d to calculate λ, we must expect that their errors will contribute to an experimental
error in λ. Estimate the error in λ using
λ
δd
d
q
d
3
−1 ym
cos tan
(xδym )2 + (ym δx)2
δλ2 =
m
x
q
δλ1 =
δλ =
(δλ1 )2 + (δλ2 )2 .
Calculate the maximum number of fringes that you are expected to observe with the
grating. (Hint sin θ ≤ 1). Do you observe all of the expected fringes?
Checkpoint
What are gratings useful for?
6.2.3
Part 3: The Fresnel Zone Plate
In the Fraunhofer formalism light is represented by plane waves, and the distance between
light-source and scattering object or scattering object and observer is assumed to be very
large compared to the dimensions of the obstacle in the light path. If you drop these
conditions, the light phenomena observed are described by the Fresnel formalism and the
light waves are represented by spherical waves rather than plane waves.
Figure 6.9 shows the spherical surface corresponding to the primary wave front at some
arbitrary time t after it has been emitted from S at t = 0. As illustrated the wave front is
divided into a number of annular regions. The boundaries between these regions correspond
to the intersections of the wave front with a series of spheres centered at P and having radius
r0 + 12 λ, r0 + λ, r0 + 32 λ, etc.
76
CHAPTER 6: EXPERIMENT 4
Figure 6.9: The Fresnel Zones. The surface of the spherical wavefront generated at point
S in the figure above has been divided into several ‘Fresnel Zones’. Each area is comprised of
points that are close to the same distance from point P and thus all the secondary wavelets
emanating from within the same Fresnel Zone will add constructively at P.
These are Fresnel zones or half-period zones. The sum of the optical disturbances from
all m zones at P is
E = E1 + E2 + . . . + Em
(6.8)
Checkpoint
What is the difference between Fraunhofer and Fresnel scattering?
The path length for the light passing through each consecutive zone increases by λ/2
so the phase changes by π and the amplitude, Eζ , of zone ζ alternates between positive
and negative values depending on whether ζ is odd or even. As a result contributions from
adjacent zones are out of phase and tend to cancel.
The surface of the spherical wavefront generated at point S in Figure 6.9 has been
divided into several ‘Fresnel Zones’. Each area is comprised of points that are close to the
same distance from point P and thus all the secondary wavelets emanating from within the
same Fresnel Zone will add constructively at P.
This suggests that we would observe a tremendous increase in irradiance (intensity) at P
if we remove all of either the even or the odd zones. A screen which alters the light, either
in amplitude or phase, coming from every other half-period is called a zone plate. Examples
are shown in Figure 6.8. Suppose that we construct a zone plate which passes only the first
20 odd zones and obstructs the even ones,
E = E1 + E3 + . . . + E39
77
(6.9)
CHAPTER 6: EXPERIMENT 4
Zone
Plate
rm
Rm
S
r0
O
P
Figure 6.10: A schematic diagram showing how travel distance can be determined for light
passing through a zone plate at a distance Rm from the optical axis. If this distance is within
ρ0 + r0 + (m ± 14 )λ, the zone plate is transparent; otherwise it is opaque.
and that each of these terms is approximately equal. For a wavefront passing through
a circular aperture the size of the fortieth zone, the disturbance at P (demonstrated by
Fresnel but not obvious) would be E1 /2 with corresponding intensity I ∝ (E1 /2)2 . However,
with the zone plate in place E ∼
= 20E1 at P. The intensity I of the light at P has been
increased by a factor of 1600 times. The zone plate acts as a lens with the focusing being
done by interference rather than by refraction!
To calculate the radii of the zones shown in Figure 6.8, refer to Figure 6.10. The outer
edge of the mth zone has radius Rm . By definition, a wave which travels the path S-Rm -P
must arrive out of phase by m2 λ with a wave which travels the path S-O-P, that is,
Path difference = (ρm + rm ) − (ρ0 + r0 ) =
According to the Pythagorean theorem ρm =
q
mλ
.
2
2 + ρ2 and r =
Rm
m
0
q
(6.10)
2 + r 2 . Expand both
Rm
0
2
these expressions using the binomial series and retain only the first two terms, ρm ≈ ρ0 + 2Rρm0
2
and rm ≈ r0 + 2Rrm0 . Substituting into Equation (6.10) gives the criterion the zone radii must
satisfy to maintain the alternating λ/2 phase shift between zones,
mλ
R2
R2
2
= (ρm + rm ) − (ρ0 + r0 ) ≈ m + m and Rm
≈
2
2ρ0
2r0
1
ρ0
mλ
.
+ r10
(6.11)
The width of zone m is proportional to √1m . Since the circumference (length) of the ring is
√
2πRm ∼ m, the area and transmitted intensity is the same for all m. For m = 1 we may
rewrite Equation (6.11) as
1
1
λ
1
+
= 2 =
(6.12)
ρ0 r0
R1
f1
78
CHAPTER 6: EXPERIMENT 4
to put it in a form identical to the thin lens equation ( d1o + d1i = f1 ) with primary focal length
R2
f1 = λ1 . Once the zone plate is made, the ring radii are fixed so that the focal length is
different for every wavelength. This property might be utilized in a spectrometer.
The spacing of the zones on the Fresnel Zone Plate are very fine. If a narrow beam is
passed through the plate it will act as a diffraction grating. Put the Fresnel Zone Plate in
the red laser path and observe the diffraction pattern. Move the plate back and forth so
that you observe the results when light hits the center and the outside of the plate. Is the
slit separation smaller on the outside or center of the plate? What have you observed that
supports this answer? Can you sketch the zones in your Data? This kind of experiment used
with X-rays allows us to quantify the properties of crystalline solids.
Measure the primary focal length of your setup’s zone plate. Do this by centering the
laser beam on the double concave lens which will diffuse the beam and generate on the screen
a uniformly illuminated circle. The divergent beam emanating from the double concave lens
now acts as a point source or ‘object’. Now place the zone plate between the lens and the
screen, and change the position of the screen along the direction of the beam to observe the
refocusing of the laser beam. Measure the two quantities ρ0 and r0 (Figure 6.10) for at least
2 different initial values of r0 and then use Equation (6.12) to calculate f1 . Don’t forget
your units. How far can you move the zone plate before the spot is out of focus? You must
consider all of these locations when estimating your errors.
Often zone plates are made of plastic material or metal with adjacent rings supported
by spokes so that the transparent regions are devoid of any material. These will function as
lenses in the range from ultraviolet to soft (low energy) X-rays (1 to 1000 Å) where ordinary
glass is opaque. Zone plates have also been used to focus low energy neutron beams.
Checkpoint
What is a Fresnel half-period zone? Sketch a zone plate. What are the zone plates
used to do?
6.3
Analysis
Calculate the difference between the manufacturer specified double-slit spacing and the mean
of your measurements
∆ = Measured - Manufacturer
(6.13)
Calculate the exptected error in this differences using
σ=
q
(δMeasured)2 + (δManufacturer)2 .
Repeat for the measured green laser wavelength versus 532.0 nm.
79
(6.14)
CHAPTER 6: EXPERIMENT 4
For each, is ∆ < 2σ? Is ∆ > 3σ? Recall that ∆ > σ about 1:3 and ∆ > 2σ about
1:22 just from random fluctuations; these probabilities are too large for us to assert that
the compared two numbers are not equal. But ∆ > 3σ only 1:370 due only to random
fluctuations, so differences this large suggest that we conclude that the two numbers are
indeed different; statistics cannot tell us why, however.
Can you think of anything in the three experiments that might reasonably affect the
measurements that we have not already included in our measurement errors? Discuss each
of these using complete sentences and paragraphs. In your view is it more likely that the
theory that has survived for a hundred years of professional tests is false or that you have
made some mistake or overlooked some significant sources of error that might explain your
nonzero difference(s)?
6.4
Conclusions
What physics have your experiments supported? Contradicted? What have you investigated
and failed to resolve? Is mλ = d sin θ? What do these symbols mean? Does light exhibit
wave properties? If so, which properties? Do Fresnel zone plates focus light? Don’t forget
that we communicate using complete sentences.
Have you measured anything that might be of value in the future? If so, state what they
are, give your measured values, their errors, and their units.
6.4.1
References
Sections of this write up were taken from:
• Bruno Gobi, Physics Laboratory: Third Quarter, Northwestern University
• D. Halliday & R. Resnick, Physics Part 2, John Wiley & Sons.
• R. Blum & D. E. Roller, Physics Volume 2, Electricity, Magnetism, and Light, HoldenDay.
• E. Hecht/A. Zajac, Optics, Addison-Wesley Publishing
80
CHAPTER 6: EXPERIMENT 4
6.5
APPENDIX: The Helium-Neon Laser
The laser (Light Amplification by Stimulated Emission of Radiation) is a source of radiation
capable of delivering intense coherent electromagnetic fields. The laser beam coherence is
manifest in two ways:
1) it is highly monochromatic, and
2) it is spatially coherent;
the emitted light has a nearly constant wavefront and directionality. The special characteristics of laser radiation are directly attributable to the phenomenon of stimulated emission
and to the positive feedback mechanism provided by the cavity structure. Figure 6.11, a
schematic diagram of a typical gas laser, highlights the major elements of a gas system. It
consists of an active medium (lasing material), which in this case is a gas, but may consist of
a solid or a liquid. A power supply pumps energy into the active medium, exciting the atoms.
To achieve oscillations mirrors are placed perpendicular to the axis of the active medium to
form an optical resonant cavity. Stimulated emission in the active medium results in the
required amplification, whereas the mirrors supply the feedback required for regenerative
action and oscillation. The rest of this appendix explains these concepts in greater detail.
(a)
(b)
Figure 6.11: Two energy diagrams illustrating photo-emission and photo-absorption. In
the first case an atom gives its energy of excitation to the creation of a photon. In the second
case a photon collides with an electron and promotes it to a more energetic atomic orbit.
Checkpoint
Which ones are the unique properties of light emitted by a laser?
6.5.1
Atomic Levels
The atom (see 8th lab) consists of a small heavy nucleus surrounded by orbiting electrons.
Quantum Mechanics describes the orbits of the electrons as standing waves. Consequently,
81
CHAPTER 6: EXPERIMENT 4
Figure 6.12: Two energy diagrams illustrating photo-absorption and stimulated emission.
If the atom is initially not excited, the photon excites the atom. If the atom is initially
excited, the incident photon stimulates the emission and both photons are identical to the
incident photon.
the electrons belonging to a specific orbit have a discrete energy value. Of the infinite number
of allowed electron orbits (energy levels), only the lowest energy levels are filled when the
atom is in the ground state. When the atom is excited, electrons are transferred from the
low energy stable orbits to higher states, leaving vacancies in the original orbits. The excited
atom will then decay (the electron in the excited state jumps back down to lower levels) with
a time constant characteristic of the level. (The time constant of an atomic level has exactly
the same meaning as the time constant of an RC circuit.) This time is usually around 10−8 s,
but in some cases it is on the order of a second (it is then called metastable). Figure 6.11 in
the 8th lab shows, as an example, the energy levels of hydrogen. For the sake of simplicity,
we shall consider an atom having only two possible energy states: an upper state E2 and
a lower state E1 as shown in Figure 6.12. If the atom is in the upper state (excited state)
and makes a transition to the lower state, then ∆E energy can be emitted in the form of
radiation with the frequency
E2 − E1
(6.15)
ν=
h
(h is the Planck constant: h = 6.634 × 10−34 J·s). On the other hand, if the atom is initially
in the lower energy state, E1 , and makes a transition to the higher state, E2 , then energy
and hence radiation with a frequency given by Equation 6.15, must be absorbed. Albert
Einstein showed that emission (transition from E2 → E1 ) can occur in two ways:
1) by the atom randomly changing to the lower state with lifetime τ . This is called
spontaneous emission and is contrasted with absorption in Figure 6.11.
2) by a photon having an energy equal to the energy difference between the two levels
interacting with the atom in the upper state and causing it to change to the lower
state with the creation of a second photon. This process can be thought of as the
converse of absorption and is known as stimulated emission. See Figure 6.12.
There are two very important points about stimulated emission upon which the properties
82
CHAPTER 6: EXPERIMENT 4
of laser light depend. First, the photon produced by stimulated emission is of almost equal
energy to that which caused stimulated emission and hence the light waves associated with
them must be of nearly equal frequency. Second, the light waves associated with the two
photons are in phase - they are said to be coherent. In the case of spontaneous emission
the random emission of photons results in waves of random phase and the light is said to be
incoherent.
Checkpoint
Sketch an energy level diagram of an atom. Indicate one transition and the frequency
of the transition. How many possible energy levels are present in an atom?
Checkpoint
What does it mean that a level of an atom has a lifetime of 10−8 s? What is a
metastable level (or state) of an atom?
Checkpoint
What is the difference between spontaneous emission and stimulated emission?
6.5.2
Population Inversion
Consider two two-level energy systems representing an atom in an upper and lower state.
Suppose that a photon of energy equal to the energy difference between the two levels
approaches the two atoms, then which event is more likely to take place, absorption or
stimulated emission? Einstein showed that under normal circumstances, both processes are
equally probable. A larger population (number of atoms) in the upper level will result in
stimulated emission dominating, while if there are more atoms in the lower level, there will be
more absorption than stimulated emission. Normally, there are more atoms in the lower level,
since in equilibrium such a system tends to minimize its energy (remember your chemistry!)
Hence, under the normal thermodynamic circumstances absorption will dominate. However,
if we can somehow put energy into the system in such a way that there are more atoms in
the upper level, then stimulated emission will dominate. When we have such a situation,
where we have put more atoms into the upper level than there are in the lower level, we have
achieved population inversion.
83
CHAPTER 6: EXPERIMENT 4
Figure 6.13: Two energy diagrams illustrating how an excited He atom collides with
an unexcited Ne atom; the collision transfers the excitation from the He to the Ne’s longlived metastable state. Identical collisions occurring throughout the gas mixture causes more
excited Ne atoms than ground-state Ne atoms.
6.5.3
Excitation of Atoms
Atoms can be excited by electrical discharge, radio frequency signals (RF), heat, chemical
reactions, collisions with electrons, or collisions with other atoms. The excitation by collision
(two different kinds) is the most relevant process in a gas laser.
1. Collisions of the first kind involve the interaction of an energetic electron with an atom
in the ground state. The impact of the electron causes it to exchange some of its energy
with the atom and the latter becomes excited. This process can be represented by an
equation similar to the one used in chemical reactions, i.e.
He + e1 → He∗ + e2
(6.16)
the * signifies that the He is in an excited state. The kinetic energy of the electron
before and after the collision is designated by e1 and e2 respectively. Since all electrons
are identical, we cannot know whether two electrons exchange places in the collision;
indeed, many argue that the distinction is meaningless.
2. A collision of the second kind involves the collision of an excited atom in a metastable
state with another atom of a different element in an unexcited state, the final result
84
CHAPTER 6: EXPERIMENT 4
being a transfer of energy from the metastable state to the unexcited atom, thus
exciting it. The metastable atom therefore loses energy and reverts to a lower state.
An example of a collision of the second kind is represented by the following equation,
He∗ + Ne → He + Ne∗ .
(6.17)
The excited Ne atom is then ready to emit a photon and to return to its ground-state.
Checkpoint
How do you excite an atom?
6.6
The Helium-Neon Laser
Figure 6.13 shows juxtaposed the energy levels of He and Ne. Only the levels relevant to
the operation of this laser are indicated. The boxes in the figure indicate groups of tightly
spaced levels (energy bands) rather than sharp single ones, and the letter M indicates that
the level is metastable (long lifetime).
The beam of light of the Helium-Neon Laser is produced by the stimulated emission of
radiation produced in the decay of excited electrons in the 3S and 2S levels of neon. These
levels of the neon atom, however, are not easily excited because the outer orbitals have a
much greater probability of being if excited before them. Instead, energy supplied by an
electrical current (in the form of energetic electrons) is stored in the metastable levels of
helium and later transferred by collisions of the second kind to neon. The two 21 S and 23 S
metastable levels of helium are very close in energy to the 2S and 3S levels of neon which
we wish to populate with excited electrons. Therefore, collisions between helium and neon
(which are ensured by selecting a ratio of He to Ne gas of 10 to 1) leave the 2S and 3S
levels of neon well populated. The observed light of the HeNe laser is generated only by the
decay of 3S electrons to the 2P state (632.8 nm). Sustained operation of the laser is ensured
by the He/Ne ratio and by the fact that the lower level (2P) decays 10 times faster (decay
time t = 10−8 s) than the upper (3S) one (t = 10−7 s). (So that basically all electrons that
decay to the 2P level undergo further decay). Light generated in any other forms of decay is
suppressed (for example by inserting a prism into the cavity, which diverges the unwanted
frequencies away from the axis of the laser tube).
We have so far described how energy is pumped into the plasma to achieve population
inversion. To have an operating laser we still need signal amplification and the proper
feedback to sustain the oscillation. This will be discussed next.
85
CHAPTER 6: EXPERIMENT 4
Figure 6.14: A schematic diagram of a resonant cavity filled with a plasma tube. The light
gain medium in the cavity replaces cavity losses to sustain the laser oscillator.
Checkpoint
In a He-Ne laser, which gas emits the observed transition of 632.8 nm?
Checkpoint
How are the Ne atoms excited in a He-Ne laser?
Checkpoint
What is the meaning of “population inversion” when explaining the operation of a
laser?
Checkpoint
How do you eliminate radiation of unwanted wave length from a laser beam?
Checkpoint
Why is the ratio of the He- to Ne- gas, 10 to 1, in the He-Ne laser?
6.6.1
Amplification and feedback
We have indicated above that the observed light of the HeNe laser is generated only by the
transition of 3S electrons to the 2P state (632.8 nm). In this process of spontaneous emission,
a great part of the radiation propagates away from the cavity in arbitrary directions and
is lost. (Though some will be absorbed by a 2P state of neon and will repopulate the 3S
86
CHAPTER 6: EXPERIMENT 4
level.) A small portion, however, will strike other neon atoms (excited to the 3S level) and
cause stimulated emission. Of the photons emitted here, however, only the small portion
emitted in a direction perpendicular to the mirrors may stay in the cavity and contribute to
the amplification process.
Upon successive reflections by the mirrors, light traveling through the laser medium is
further coherently amplified. Since the HeNe laser light amplification is only 1.02 on each
pass of the beam from one mirror to the other, all losses must be kept below 2%. Losses in
the cavity formed by plane-parallel mirrors will be extremely sensitive to the parallelism of
the two mirrors. Slight angular misalignment might result in the reflected beam missing the
opposite mirror and lead to excessive loss and difficulties in attaining oscillation. Even under
perfect parallelism, it can be shown that a resonator formed by plane-parallel mirrors has
higher diffraction losses than a cavity formed by various combinations of plane and curved
mirrors. Since the laser tube and the mirrors form an optical resonant cavity, the optical path
length between successive reflections of the mirror must be an integral number of wavelengths
to produce reinforcement of the wave. This arrangement of mirrors was familiar long before
the advent of lasers and is known as the Fabry-Perot interferometer.
Checkpoint
What physical effect is responsible for the amplification of the light signal of a laser?
6.6.2
The Laser’s Mirrors
To produce an external laser beam, the mirror at the front of the laser tube is a partial
reflector which reflects 99% of the light and transmits approximately 1%. The mirror at the
back end of the laser tube has a higher reflectivity and reflects about 99.9% of the light while
transmitting less than 0.1%.
Laser mirrors are always made by successive deposition of materials with high and low
refractive indices onto substrates of the highest optical quality. By making the optical
thickness of each layer a quarter of a wavelength thick, very high reflectivities can be achieved.
The mirror is the most expensive part of a laser - often good quality mirrors are made of 20
or more layers of dielectric material.
Checkpoint
Why is the plasma tube of a gas laser enclosed by two parallel mirrors normal to the
axis of the tube? How do you extract the light from a laser?
87
CHAPTER 6: EXPERIMENT 4
Figure 6.15:
A sketch of light propagating through an excited active gain medium.
Spontaneous emissions with a radial component quickly leave the cavity after very little
amplification; contrarily, the axial mode gets amplified continuously and repetitively.
6.6.3
Mode Configuration
A beam of light propagating down the optical axis of the laser will be amplified, and providing
sufficient gain is available, will emerge from the laser output mirror. Generally speaking, a
photon traveling at right angles to the optical axis will not be amplified to form a laser beam.
Although it may cause many stimulated emissions, there will not be a large enough number to
overcome all losses or, in other words, the gain will be inadequate. However, in the situation
where a wave is traveling only slightly off axis, the wave may be able to zig-zag or “walk”
between the mirrors a sufficient number of times to produce enough gain to overcome the
losses. This produces the laser output, which consists of a variety of complicated patterns.
These patterns are the result of the laser operating in what is referred to as transverse
modes. (Some light rays are not aligned on the laser’s axis.) Such modes are designated by
the notation TEMpq modes (TEM standing for transverse electromagnetic).
The most commonly used mode is the TEM00 mode. A laser operating in this mode has
a Gaussian flux density pattern over the beam cross section. This pattern - a single disk
area - produces a single spot of light.
Checkpoint
What does the beam spot look like for a laser operating in the TEM00 mode?
88
CHAPTER 6: EXPERIMENT 4
6.6.4
References
Sections of this write up were taken from:
• M.J. Beesley, Lasers and Their Applications, Taylor Z Francis Ltd., and Barnes &
Noble Inc., 1971.
• Edited by S.S. Charschan, Lasers in Industry, Western Electric Series, Van Nostrand
Reinhold Company.
6.7
Laser Safety
WARNING
Lasers emit extremely bright light. Laser light can damage your eyes. Lasers
exist that cut and weld metals; however, this lab does not contain them. Care must
be exercised to avoid exposing your eyes to the laser’s light.
Powerful pulsed lasers are used for welding and are also capable of drilling holes in
metal. High-power lasers are used in surgery, in resister trimming, in non-destructive testing,
and even in static and dynamic art exhibits. The laser used in the lab has a nominal
0.5 mW visible output which places the device within the Class III category, as defined by
the Department of Health, Education, and Welfare for laser safety. To insure absolute safety,
however, the following precautions and safety procedures MUST be observed.
1) Treat all laser beams with great respect.
2) Never look into the laser window (even when turned off) or stare into the beam (on
axis) with either the naked eye or through binoculars or a telescope at a distance.
3) Do not rely on sunglasses as eye-protecting devices.
4) Never point the laser beam near anyone else’s eyes.
5) Cover all windows to protect passers-by.
6) Never leave lasers unattended while activated. If not in use disconnect A.C. power
cable.
7) Room illumination in the work area should be as high as is practicable to keep
the eye pupil small and reduce the possibility of retinal damage due to accidental
exposure.
8) Remove all superfluous and highly reflective objects from the beam’s path. These
include rings, watches, metallic watchbands, shiny tools, glassware, etc.
89
CHAPTER 6: EXPERIMENT 4
90
Chapter 7
Experiment 5:
Diffraction of Light Waves
WARNING
This experiment will employ Class III(a) lasers as a coherent, monochromatic light
source. The student must read and understand the laser safety instructions on
page 89 before attending this week’s laboratory.
7.1
Introduction
In this lab the phenomenon of diffraction will be explored. Diffraction is interference of a
wave with itself. According to Huygen’s Principle waves propagate such that each point
reached by a wavefront acts as a new wave source. The sum of the secondary waves emitted
from all points on the wavefront propagate the wave forward. Interference between secondary
waves emitted from different parts of the wave front can cause waves to bend around corners
and cause intensity fluctuations much like interference patterns from separate sources. Some
of these effects were touched in the previous lab on interference.
General Information
We will observe the diffraction of light waves; however, diffraction occurs when any
wave propagates around obstacles. Diffraction and the wave nature of particles leads
to Heisenberg’s Uncertainty Principle and to the very reason why atoms are the sizes
that they are.
In this lab the intensity patterns generated by monochromatic (laser) light passing
through a single thin slit, a circular aperture, and around an opaque circle will be predicted
and experimentally verified. The intensity distributions of monochromatic light diffracted
91
CHAPTER 7: EXPERIMENT 5
m=4
m=3
m=2
y
m=1
m=0
a
x
m = -1
m = -2
Diffraction
Pattern
m = -3
m = -4
Plane Wave
Figure 7.1: A sketch of a plane wave incident upon a single slit being diffracted and the
resulting intensity distribution. The intensity is on a logarithmic scale; since our eyes have
logarithmic response, this much more closely matches the apparent brightness of the respectve
dots. Keep in mind that this week we are concerned with the dark intensity MINIMA and
that m = 0 is NOT a minimum.
from the described objects are based on:
1. the Superposition Principle,
Intensity vs. Position
2. the wave nature of light Disturbance:
1
(a) Amplitude: A = A0 sin(ωt + ϕ)
(b) Intensity: I ∝ (
P
0.8
A)2 ,
0.6
3. Huygen’s Principle - Light propagates in
such a way that each point reached by
the wave acts as a point source of a new
light wave. The superposition of all these
waves represents the propagation of the
light wave.
0.4
0.2
0
-7
-5
-3
-1
1
3
5
7
y (cm)
All calculations are based on the assumption
that the distance, x, between the slit and the Figure 7.2: A graphical plot of an examviewing screen is much larger than the slit width ple diffraction intensity distribution for a
a:, i.e. x >> a. This particular case is called single slit.
Fraunhofer scattering. The calculations of this
92
CHAPTER 7: EXPERIMENT 5
type of scattering are much simpler than the Fresnel scattering in which case the x >> a
constraint is removed.
Checkpoint
What is the difference between Fraunhofer and Fresnel scattering?
Checkpoint
Are the eyes sensitive to the amplitude, to the phase, or to the intensity of light? Are
the eyes’ response linear, logarithmic, or something else?
7.1.1
Part 1: Diffraction From a Single Slit
A narrow slit of infinite length and width a is
illuminated by a plane wave (laser beam) as shown
in Figure 7.1. The intensity distribution observed (on
a screen) at an angle θ with respect to the incident
direction is given by Equation (7.1). This relation is
derived in detail in the appendix and every student
must make an effort to go through its derivation.
The mathematics used to calculate this relation are
very simple. The contributions from the field at each
small area of the slit to the field at a point on the
screen are added together by integration. Squaring
this result and disregarding sinusoidal fluctuations in
time gives the intensity. The main difficulty in the
calculation is determining the relative phase of each
small contribution. Figure 7.2 shows the expected
shape of this distribution; mathematics can describe
Figure 7.3: A photograph of Pasco’s this distribution,
OS-8523 optics single slit set. We are
sin α 2
πa
I(θ)
interested in the single slits at the top
=
with α =
sin(θ),
(7.1)
I(0)
α
λ
right and the circular apertures at the
top left.
where a is the width of the slit, λ is the wavelength of
the light, θ is the angle between the optical axis and
the propagation direction of the scattered light, I(θ) is the intensity of light scattered to
angle θ, and I(0) is the transmitted light intensity on the optical axis. When θ = 0, α = 0,
and the relative intensity is undefined (0/0); however, when θ is very small and yet not zero,
the relative intensity is very close to 1. In fact, as θ gets closer to 0, this ratio of intensities
93
CHAPTER 7: EXPERIMENT 5
gets closer to 1. Using calculus we describe these situations using the limit as α approaches
0,
sin α
lim
= 1.
α→0 α
Although 0/0 might be anything, in this particular case we might think that the ratio is
effectively 1; this is the basis for the approximation sin θ ≈ θ when θ << 1 radian. Certainly,
the intensity of the light on the axis is defined, is measurable, and is quite close to the
intensity near the optical axis. The numerator of this ratio can also be zero when the
denominator is nonzero. In these cases the intensity is predicted and observed to vanish.
These intensity minima occur when 0 = sin α for each time
πm = α and mλ = a sin θ for m = ±1, ±2, . . .
(7.2)
Figure 7.4: A sketch of our apparatus showing the view screen, the sample slide, the laser,
and the laser adjustments. Our beam needs to be horizontal and at the level of the disk’s
center.
We might note the similarity between this relation and the formula for interference
maxima; we must avoid confusing the points that for diffraction these directions are intensity
minima and for diffraction the optical axis (m = 0) is an exceptional maximum instead of
an expected minimum.
This relation is satisfied for integer values of m. Increasing values of m give minima at
correspondingly larger angles. The first minimum will be found for m = 1, the second for
m = 2 and so forth. If is less than one for all values of θ, there will be no minima, i.e. when
the size of the aperture is smaller than a wavelength (a < λ). This indicates that diffraction
is most strongly caused by protuberances with sizes that are about the same dimension as a
wavelength.
Four single slits (along with some double slits) are on a disk shown in Figure 7.3 photograph of Pasco’s OS-8523 optics single slit set. We are interested in the single slits at the
top right and the circular apertures at the top left.. This situation is similar to the one
diagrammed in Figure 7.1. To observe diffraction from a single slit, align the laser beam
94
CHAPTER 7: EXPERIMENT 5
parallel to the table, at the height of the center of the disk, as shown in Figure 7.4. When the
slit is perpendicular to the beam, the reflected light will re-enter the laser. The diffraction
pattern you are expected to observe is shown in Figure 7.5.
Figure 7.5: Observed Diffraction Pattern. The pattern observed by one’s eyes does
not die off as quickly in intensity as one expects when comparing the observed pattern with
the calculated intensity profile given by Equation (7.1) and shown in Figure 7.2. This is
because the bright laser light saturates the eye. Thus the center and nearby fringes seem to
vary slightly in size but all appear to be the same brightness.
Observe on the screen the different patterns generated by all of the single slits on this
mask. Note the characteristics of the pattern and the slit width for each in your Data. Is it
possible from our cursory observations that mλ = a sin θ? If a quick and cheap observation
can contradict this equation, then we need not spend more money and time.
Calculate the width of one of the four single slits. This quantity can be calculated from
Equation (7.2) using measurements of the locations of the intensity minima. The wavelength
of the HeNe laser is 6328 Å, (1 Å= 10−10 m). The quantity to be determined experimentally
is sin θ. This can be done using trigonometry as shown in Figure 7.6.
Measure the slit width using several intensity minima of the diffraction pattern. Place a
long strip of fresh tape on the screen and carefully mark all of the dark spots in the fringes.
Be sure to record the manufacturer’s specified slit width, a. Avoid disturbing the laser, the
slit, and the screen until all of the minima are marked and the distance, x, between the
slit and the screen is measured. Is your screen perpendicular to your optical axis? Remove
the slit and circle the undeflected laser spot. Ideally, this spot is exactly the center of the
diffraction pattern. Make a table in your Data and record the order numbers, m, and the
distances, ym , between the optical axis and the dark spots. It is more accurate to measure
the distance 2 ym between the two mth minima on opposite sides of the axis; you might wish
to avoid this additional complication. Note the units in the column headings and the errors
in the table body.
Enter your data table into Vernier Software’s Ga3 graphical analysis program. A suitable
setup file for Ga3 can be downloaded from the lab’s website at
http://groups.physics.northwestern.edu/lab/diffraction.html
Otherwise, change the column names and units to represent your data. Add a calculated
column to hold your measured slit widths. Enter the column name and appropriate units
and type
95
CHAPTER 7: EXPERIMENT 5
R
y
x
Figure 7.6: A sketch of the trigonometric functions sine and tangent.
“m” * 632.8 * x / (c * “ym”)
into the Equation edit control. Use the “Column” button to obtain the quoted values; choose
your column names instead of mine. Instead of “x” type the number of cm, m, etc. between
your screen and slit; use the same units for x as for ym so that they cancel in the above ratio.
What units remain to be the units of a? If you like, you can use the value “c” to convert
these units to nm (c = 1), µm (c = 1000), mm (c = 1000000), or m (c = 109 ). Be sure to use
the correct units in the column heading to represent your numbers. Plot your slit widths
on the y-axis and the order number on the x-axis. Click the smallest number on the y-axis
and change the range to include 0. Does it look like all of your data are the same within
your error? If so, draw a box around your data points and Analyze/Statistics. Move the
parameters box off of your data points.
Interpret the “mean” ā of your data to be the best estimate of the slit’s true width and
the “std.dev” to be the best estimate of each data point’s error, sa . Estimate the error in
the mean to be the standard error
sa
sā = √ .
N
Specify your best estimate of slit width as a = (ā ± sā ) U.
Checkpoint
The relation of sin2 α/α2 for α = 0 is an undefined expression of 0/0. What is the
limit of this relation for the limit α → 0?
Checkpoint
Which relation gives the position of the diffraction minima for a slit of width a,
illuminated with plane wave light of wavelength λ?
96
CHAPTER 7: EXPERIMENT 5
Checkpoint
If you want to sharpen up a beam spot by inserting a narrow vertical slit into the
beam, will the beam spot get more and more narrow as you close the slit? Explain.
7.1.2
Part 2: Diffraction by a Circular Aperture
For a circular hole of diameter, d, the diffraction pattern of light with wavelength λ consists
of concentric rings, which are analogous to the bands which we obtained for the single slits.
The pattern for this intensity distribution can be calculated in the same way as for the single
slit (see Appendix), but because the aperture here is circular, it is more convenient to use
cylindrical coordinates (z, ρ, φ). The superposition principle requires us to integrate over a
disk, and the result is a Bessel function. The condition for observing a minimum of intensity
is found from the zeroes of the Bessel function,
λ
sin θ = km .
d
(7.3)
For the first order (m = 1) minimum k1 = 1.22. Higher order minima will have larger km
coefficients.
The disk provided with the apparatus has circular openings of two different diameters.
Put the apertures in the laser beam one at a time and observe how the diameter of the dark
rings depends on the aperture diameter. Record your observations in your Data and choose
the configuration which gives the best diffraction pattern for detailed study.
Calculate the diameter of the aperture by measuring the distance between the center
of the dot pattern and the first minimum and by using Equation (7.3). To make this
measurement accurately, make the distance between the object and the screen large; you
may choose to use the wall as your screen. The radius can be measured most accurately
by measuring the dark ring’s diameter and dividing by 2. The radius then determines
sin θm = rxm as shown in Figure 7.6. If the dark circle is irregular, use a typical value instead
of the largest or smallest radius and consider its shape when estimating the error. Measure
the distance, x, between the screen and the aperture. Don’t forget to include your units and
errors.
The roundoff error in k1 is limited to ±0.005 and you have estimated errors for x and
r1 . The error in our wavelength is much smaller than these so estimate the error in aperture
diameter using
v
u
u δr1
1.22λx
d≈
and δd = dt
r1
r1
!2
0.005
+
1.22
2
.
(7.4)
Measure the value of the constant km in front of the ratio λd in Equation (7.3) for
the second order minimum, m = 2, and the third order minimum, m = 3. Do this by
using as aperture diameter d the value previously obtained above and by measuring sin θ
97
CHAPTER 7: EXPERIMENT 5
corresponding to the second minimum and then the third minimum,
v
u
u δd
drm
and δkm = km t
km ≈
λx
d
!2
δrm
+
rm
!2
.
In measuring the constant km you are determining the zeroes of a function called a Bessel
function that seems to describe situations with cylindrical symmetry.
Checkpoint
Beams of particles act like waves with very short wavelengths when scattered by
protuberances such as other particles. If a target of Pb and one of C are bombarded
with a beam of protons, which target will show the sharpest diffraction pattern, the
large size Pb target or the small C one? (Hint: The pattern due to an aperture is
identical to the pattern caused by its photographic negative: a disk in empty space.)
Checkpoint
What size object will generate an observable diffraction pattern if placed in the path
of light with wavelength λ?
Checkpoint
What is responsible for the factor 1.22 in Equation (7.3)?
7.1.3
Part 3: The Poisson Spot
Figure 7.7: A sketch illustrating the optical beam line used to observe the Poisson spot in
the center of a sphere’s shadow.
98
CHAPTER 7: EXPERIMENT 5
Historical Aside
In 1818 Augustin-Jean Fresnel entered a competition sponsored by the French Academy
to try clear up some outstanding questions about light. His paper was on a wave theory
of light in which he showed that the refraction and reflection of light and all of their
characteristics could be explained if we only allowed light to be treated as a wave. His
theory even explained the results of Young’s double-slit experiment. This was about
30 years after Sir Isaac Newton presented a corpuscle theory of light in which light
particles moved from a source to a destination but could be bent by material surfaces.
Everyone knows to hide behind a rock or a tree if someone is throwing stones or shooting
bullets at him since the projectiles will either be stopped by the obstacle or pass harmlessly
by. One is not so safe from waves in a swimming pool, however, because waves will bend
around obstacles having the size of their wavelengths or smaller.
Historical Aside
Many scientists at the meeting were having problems with Fresnel’s paper because
everyone can see that objects cast shadows. Simeon Denis Poisson, one of the judges,
was particularly disturbed by Fresnel’s paper and he used wave theory to show that if
light is to be described as a wave phenomenon, then a bright spot would be visible at
the center of the shadow of a circular opaque obstacle, a result which he felt proved
the absurdity of the wave theory of light.
This surprising prediction, fashioned by Poisson as the death blow to wave theory, was
almost immediately verified experimentally by Dominique Argo, another member of the
judges committee. The spot actually exists! The spot is still called the Poisson spot despite
Argo’s having discovered it. I guess this just goes to show that some of our mistakes will
never be lived down. . .
Historical Aside
Fresnel won the competition, but it would require James Clerk Maxwell (sixty years
later) to locate the medium in which the waves of light propagate.
In less than 60 seconds you can now settle a controversy that has preoccupied the minds
of the brightest philosophers and scientists for centuries. Is light described as a stream of
particles or as a wave phenomenon? In other words, does the Poisson spot exist?
Observe the Poisson Spot. Record your observations in your Data. Can you explain the
Poisson spot as constructive interference from the thin ring of light wave-fronts that just
barely miss the sphere? What must be true for all of this light to interfere constructively at
the location of the spot?
99
CHAPTER 7: EXPERIMENT 5
Use the concave (diverging) lens included with the apparatus to expand the beam slightly.
Place the circular obstacle in the beam, (see Figure 7.7), and observe on the screen, at the
center of the shadow generated by this obstacle, a bright spot - the Poisson spot! By varying
the obstacle’s position between the lens and screen, you can optimize the intensity of the
Poisson spot sort of like focusing the Fresnel zone plate.
Checkpoint
What is the Poisson spot? What does the existence of the Poisson spot demonstrate?
7.1.4
Late 20th Century View of Light
The distinction between wave and particle relies on two types of experiments. Observation
of interference phenomena demonstrates the presence of waves. Experiments which show
discrete as opposed to continuous changes such as the photoelectric effect demonstrate
particle phenomena (each photon of light knocks one electron off an atom). Light is a
wave (you observe interference) and light is also a particle called the photon (you observe
scattering and absorption of single photons). These two descriptions of light are not mutually
exclusive. The wave nature of light is observable in certain natural phenomena, whereas the
particle nature becomes apparent in other natural phenomena. The surprising conclusion
is that light behaves sometimes like a wave, and sometimes like a particle - the nature of
light depends upon the particular experimental situation. This is called the “wave - particle
duality.”
Checkpoint
What is our present view of light? Is light a wave in some medium or a stream of
particles?
7.2
Analysis
We have measured a slit width and the slit manufacturer measured the width of the same slit.
We form a NULL hypothesis by computing the difference between these two measurements,
∆ = Measured - Manufacturer.
If our measurement is the same as the manufacturer’s measurement, then this difference is
zero or NULL. Unfortunately, all measurements have error, so we cannot reasonably expect
this difference to vanish after all. A natural question to ask ourselves, then, is “How big can
100
CHAPTER 7: EXPERIMENT 5
our difference be before it is significant?” If only the experimental errors are responsible for
the nonzero result, then the difference must be bounded by our (and the manufacturer’s)
errors. We computed ∆ using two numbers containing errors (Measured and specified by a
Manufacturer) so the error in ∆ can be computed from these errors in the numbers used to
compute ∆,
q
σ = (δMeasured)2 + (δManufacturer)2 .
The manufacturer’s specified slit width has tolerance 1% so δManufacturer = 0.01 a.
If all of our errors are random, we should expect ∆ > σ with probability 1:3, ∆ > 2 σ with
probability 1:22, ∆ > 3 σ with probability 1:370, etc. Larger disagreements are progressively
less likely IF random statistical fluctuations are the only reason for the difference. Certainly
one sigma disagreements cannot be used contradict a theory that has served us well. Even
two sigma disagreements occur frequently enough that we admit the probability that we were
simply unlucky rather than our theory is wrong. This is especially true if we consider that we
might have overlooked something in our apparatus or its environment that has contributed
to our data and that we have not corrected nor compensated for. This is especially true if
one or more of our assumptions was not realized as well as we thought. This might also be
true if we were too optimistic about how well we performed the experiment; if our error is too
small, then our difference will be too many of them. (We must conclude our Analysis with
a paragraph or two that describes suspicious items such as these and how each may have
affected our data.) Three sigma and larger disagreements are sufficiently rare that we must
admit the likelihood that our measured and specified values are indeed different for some
reason. Statistics can tell us that the numbers are probably different; however, statistics
cannot tell us why. . . we must figure out why they are different for ourselves.
Since you are new to this, you have probably made some actual mistakes in processing
your data; try to find these mistakes and/or ask for help from your instructor, but don’t
waste too much time or you will not finish. Another common problem for beginners is that
they underestimate some of their errors, ask your instructor if your estimates are reasonable.
Once we have verified that no other source of error can explain ∆ > 3 σ and the effect is
reproduced consistently, we must then suggest that something is wrong with the models that
we used to produce our measured value; the theory we are testing might have a hole in it.
We have also measured the diameter of an aperture and the manufacturer has specified
a value for comparison. Each of these measurements has error also, so perform all of the
analysis above for the circular aperture data as well.
What properties of our apparatus and its environment (NOT already included in σ) might
affect the data that we have gathered? For each estimate how it might have influenced our
results. (Communicate with complete sentences.) Consider all of your observations (not just
the numerical, statistical analysis above) and proffer a brief argument about whether light
is best represented as a wave or a stream of particles.
101
CHAPTER 7: EXPERIMENT 5
7.3
Conclusions
We are now ready to state simply and briefly what our data says about light. We have already
detailed the reasons why and should not repeat those reasons here; Conclusions are merely
a series of results that our data supports. Always communicate with complete sentences to
introduce valid equations (equations are equations NOT sentences despite the fact that we
tend to read them as though they were sentences) and define the symbols (d, λ, θ, . . .) in the
equations. We need not argue why we conclude as we do at this point; however, we must
state our conclusions clearly so that our reader can understand them completely without
reading anything else in our report.
Finally, report any measured quantities that we or other experimenters might find useful
in future work. If we expect that we might re-use our slit or aperture, we might report
their measured dimensions. The Bessel functions help us describe many phenomena having
cylindrical symmetry, so the locations of their zeroes is useful information. In each case
communicate with complete sentences and include the units and errors for the measurements.
7.3.1
References
Sections of this write up were taken from:
• Bruno Gobi, Physics Laboratory: Third Quarter, Northwestern University
• D. Halliday & R. Resnick, Physics Part 2, John Wiley & Sons.
• R. Blum & D. E. Roller, Physics Volume 2, Electricity, Magnetism, and Light, HoldenDay.
• E. Hecht/A. Zajac, Optics, Addison-Wesley Publishing.
7.4
APPENDIX:
Intensity Distribution from a Single Slit
The calculation of the intensity distribution of diffraction phenomena is based upon the superposition principle and Huygen’s principle. Light is a wave and if we choose to characterize
it by the magnitude of its electric field vector, E, then it can be represented as,
E = E0 sin(ωt − kx).
102
(7.5)
CHAPTER 7: EXPERIMENT 5
If two waves with responses E1 and E2 reach
the same point P at the same time, then
the superposition principle gives the total
displacement of E as
P
E0 = E1 + E2 .
(7.6)
y
a
This total displacement depends upon the
relative phase ϕ between the two waves.
Looking at Figure 7.8, try to imagine what
happens when E2 shifts with respect to E1
(this shift is given by the phase ϕ = −kx).
By lining up peaks with peaks and valleys
with valleys, one gets a maximum displacement of the wave medium, E0 in this case. In
the
opposite case, when one lines up peaks
Figure 7.8: A schematic illustration of a
plane wave incident upon a single slit and with valleys, the response, E0 , becomes zero.
the angular coordinate used to locate points of The light intensity, I, is related to the
amplitude, E0 , by the important relation
observation.
I=
ε0 c
|E0 |2 .
2
(7.7)
Note that amplitudes must be summed first before the square is taken for the intensity,
|E0 |2 = |E1 + E2 |2 .
Figure 7.8 shows the quantities used to calculate the diffraction from a single slit of width a.
Each point in the slit along the y-direction will generate its own wavelet (Huygen’s principle)
and each of these wavelets will have the same wavelength, λ, as the incident plane wave. A
wavelet generated at point y and reaching point Note that amplitudes must be summed first
will disturb the electric field at P by the amount
Ey (t) =
with ω =
2π
T
E0
sin(ωt + ϕ(y))
a
= 2πf . The phase ϕ(y) can be determined from the path difference
ϕ(y) = k∆ =
2πy
sin θ
λ
(7.8)
so that the electric field response at P due to the wavelet emanating from y in the slit is
2πy
E0
sin ωt +
sin θ .
a
λ
Ey (t) =
(7.9)
The superposition principle determines the total amplitude at P to be the sum of the
103
CHAPTER 7: EXPERIMENT 5
contributions from every point in the slit. This is obtained by integrating,
E0
2πy
E0 Z α
sin(ωt + ϕ) dϕ
sin ωt +
sin θ dy =
E(t) =
Ey (t) dy =
λ
2α −α
−a/2
−a/2 a
E0
sin α
=−
(cos(ωt + α) − cos(ωt − α)) = E0
sin ωt.
(7.10)
2α
α
Z a/2
Z a/2
We used Equation (7.8) to change integration variables from y to ϕ and Equation (7.1) to simplify to α. Figure 7.9 shows
how this function varies with position on
a view screen. We are interested in the
light intensity; note that the
of
amplitude
sin α
Equation (7.10) is EP = E0 α , and the
intensity at P is
0.9
0.7
0.5
0.3
0.1
-10
-8
-6
-4
-2
-0.1
0
2
4
6
8
10
I(θ)
=
I(0)
ε0 c 2
EP
2
ε0 c 2
E0
2
sin α
=
α
2
,
(7.11)
where I(0) is the intensity on the optical
sin θ, a is the slit width, λ is
axis, α = πa
λ
y (cm)
the wavelength, and θ is the direction to P
from the slide. I(0) is always the maximum
Figure 7.9: The amplitude of the electric intensity of the diffraction pattern. Equafield’s oscillations at each position on the tion (7.11) will have a value of zero each time
viewscreen. The negative ‘amplitudes’ reflect a that sin2 α = 0. This occurs when α = ±mπ
half-period phase shift, but the intensity is the for integer m 6= 0 and yields Equation (7.2)
same in this case as for positive amplitudes.
for predicting the directions to points with
minimum light intensity from a single slit.
The shape of the distribution given by Equation (7.11) is shown in Figure 8.1.
-0.3
We might note as one final characteristic of diffraction that the intensity maxima are not
midway between the intensity zeroes as we might naively expect. The division by α shifts the
maxima toward the optical axis. Toward the optical axis corresponds to division by smaller
a and a larger intensity. Since dividing zero by a still yields zero, the zeroes are not shifted.
Calculus allows us to determine that the maximum intensities occur when tan αm = αm .
7.4.1
Diffraction from Double-Slit
A very similar procedure will allow us to analyze the diffraction expected from two identical
slits. Figure 7.10 shows an appropriate coordinate system; one might note the similarity to
Figure 7.8 that we used to analyze the single slit. In the double-slit case, we must integrate
over the bottom slit where − d2 − a2 < y < − d2 + a2 and then add this to the integral over the
top slit where + d2 − a2 < y < + d2 + a2 . We will make the same change of variable from y to ϕ
and the same simplification from a to α as we used for the single-slit case. Additionally, we
104
CHAPTER 7: EXPERIMENT 5
y
P
a
d
y=0
Figure 7.10: A schematic diagram illustrating a plane wave incident upon two identical
slits and the angular coordinate used to locate points of observation.
will use β =
πd
λ
sin θ to simplify from d to β in the same fashion.
"
d+a
d−a
Z
E0 Z − 2
2
E(t) =
sin
(ωt
+
ϕ(y))
dy
+
sin (ωt + ϕ(y)) dy
d−a
a
− d+a
2
2
"
#
Z (β+α)
E0 Z −(β−α)
=
sin (ωt + ϕ) dϕ +
sin (ωt + ϕ) dϕ
2α −(β+α)
(β−α)
−(β−α)
(β+α)
E0
E0
=
− cos (ωt + ϕ)
+
− cos (ωt + ϕ)
2α
2α
−(β+α)
(β−α)
105
#
CHAPTER 7: EXPERIMENT 5
E0
E(t) =
cos (ωt − (β + α)) − cos (ωt − (β − α))
2α
+ cos (ωt + (β − α)) − cos (ωt + (β + α))
=
E0 h
cos (ωt − α − β) + cos (ωt − α + β)
2α
i
− cos (ωt + α − β)) − cos (ωt + α + β)
i
E0 h
2 cos (ωt − α) cos β − 2 cos (ωt + α) cos β
2α
i
E0 h
=
cos (ωt − α) − cos (ωt + α) cos β
α
sin α
= 2E0
cos β sin(ωt)
α
=
(7.12)
We have used two trigonometric identities
cos(A − B) + cos(A + B) = 2 cos A cos B
cos(A − B) − cos(A + B) = 2 sin A sin B
the first was used once with A = ωt + α and B = β and once with A = ωt − α and B = β.
The second was used in the last step before a re-arrangement of multiplicands.
An alternate and less rigorous approach is to consider the net amplitude at P after singleslit diffraction from each slit individually to be the emission from each slit. Each of these two
waves then travels its individual distance to the screen and they interfere at P. When a plane
wave is incident on two (or more) identical slits, the amplitude of the electric field response
at P for each slit is given by Equation (7.10). Figure 7.10 shows the quantities used to
calculate the double slit diffraction intensity distribution. Since the slit widths a are equal,
we expect the intensity of the waves from them arriving at P to have equal amplitudes,
E1 = E2 = E0
sin α
.
α
(7.13)
If we measure the distances between the slits and P from the midpoint between the slits, we
can determine the relative phases for the two waves
∆
ϕ1 = k −
2
!
=−
2π 1
πd
· d sin θ = − sin θ.
λ 2
λ
(7.14)
If we let
πd
sin θ, then ϕ1 = −β and similarly ϕ2 = β.
λ
The total electric field from the slits, then, is
β=
106
(7.15)
CHAPTER 7: EXPERIMENT 5
E(t) = E1 (t) + E2 (t) = E0
= 2E0
sin α
[sin(ωt − β) + sin(ωt + β)]
α
sin α
cos β sin(ωt)
α
(7.16)
sin A+B
. The intensity distribution is found
where we have used sin A + sin B = 2 cos A−B
2
2
to be
sin α 2
I(θ)
=
cos2 β,
(7.17)
I(0)
α
where we note that the electric field amplitude for two slits on the optical axis is twice as
large as for one slit. We might note that the diffraction from two slits is the same as for one
slit, as a comparison of Equation (7.10) with Equation (7.17) easily shows. The interference
between the two slits yields fringes described by cos2 β and the diffraction merely modulates
the fringes’ peak brightness values. Examination of the definitions of β (Equation (7.17))
and α (Equation (7.1)) allows us to note that β must change faster with θ than α; after all,
the slit widths cannot exceed the separation; a = b means one big slit twice as wide instead
of two discrete slits.
Checkpoint
2
The distribution of light from two slits is represented by the product sinα α (cos β)2 .
Which one of these two terms is called the diffraction term and which one is the
interference term? Which term is responsible for the interference fringes?
General Information
This product of interference between two point sources and diffraction of one extended
source is one example of a more general strategy. When linear superposition applies,
the response of several identical extended sources can be determined by dividing the
problem into two simpler problems: solve one extended source, solve point sources
at each of their centers, and multiply the two solutions. This process is called the
convolution of the two solutions.
107
CHAPTER 7: EXPERIMENT 5
108
Chapter 8
Experiment 6: Intensity Distributions
of Diffraction Patterns
WARNING
This experiment will employ Class III(a) lasers as a coherent, monochromatic light
source. The student must read and understand the laser safety instructions on
page 89 before attending this week’s laboratory.
8.1
Introduction
In the electricity and magnetism laboratory, we observed the resonance of a RLC circuit.
This is the frequency distribution of the circuit’s current response to an AC voltage stimulus.
The Normal Distribution used in Statistics relates the probability of an observation to the
value observed. Distributions are quite common in nature so it is fitting that we should
study them.
In this lab you will observe and study the intensity distribution of light that passes
through a single slit and later a pair of identical slits; in this case we will monitor the
intensity as the angle between the original beam direction and the location of the observer
is varied. In two previous laboratory exercises you have observed these distributions using
your eyes as detectors. In this laboratory you will utilize a silicon PIN diode photodetector
to get numerical values of intensity that can be plotted and analyzed graphically. Along the
way, you will
1) learn about photodiode light intensity detectors,
2) learn to use rotary optical encoders to monitor position,
3) measure the intensity distribution of light diffracted by a single slit,
4) measure the intensity distribution of light diffracted by double slits, and
109
CHAPTER 8: EXPERIMENT 6
Intensity vs. Position
1
0.8
0.6
0.4
0.2
0
-7
-5
-3
-1
1
3
5
7
y (cm)
Figure 8.1: A graphical plot of one example intensity distribution for light transmitted
through and diffracted by a single slit.
5) evaluate the theory of light as waves using this data.
You should find that these quantitative observations have maxima and minima in precisely
the same places that we observed in the previous experiments.
The detailed theory of light transmitted through slits is described in the appendix
following the writeup for this experiment. You will be quizzed on the material in the appendix
as well as on the lab write up.
8.1.1
Intensity Distribution of Light Diffracted by Single Slits
We have learned in the fifth laboratory that the intensity distribution, I(θ), generated by
a narrow slit of width, a, and infinite length, when illuminated with coherent light of wave
110
CHAPTER 8: EXPERIMENT 6
length λ is given by
sin α
I(θ)
=
I(0)
α
2
for α =
πa
sin θ,
λ
(8.1)
θ is the angle along which direction the intensity is observed, and I(0) is the intensity of the
principal maximum. Figure 8.1 shows the expected ratio as calculated using Equation (8.1).
Minima occur when sin2 α = 0 or when
α = ±mπ and m = 1, 2, 3, . . .
(8.2)
Intensity maximum positions are given for values of α at which the derivative of Equation (8.1) becomes zero. This leads to the equation tan α = α. An approximate solution
is
1
π,
α=± m+
2
m = 1, 2, 3, . . .
(8.3)
The ratio of intensity of a secondary maximum (order m) I(θ) to the principal maximum
I(0) is
h
i
1
2
sin
m
+
π
I(θ)
1
2
(8.4)
≈ h
i2 = h
i2
1
I(0)
m+ 2 π
m + 12 π
since sin α = ±1 at the approximate maxima.
In the first part of this lab you will compare the intensity ratios calculated with Equation (8.4) to the measured ratio. Additionally, you will see how well Equation (8.1) describes
the intensity distribution details by graphing the measured intensity vs. the position of the
detector and by fitting the results to the Equation (8.1) model.
We will finish the first part by verifying that the slit width predicted by the graphical
analysis is the same as that specified by the manufacturer.
8.1.2
Intensity Distribution of Light
Transmitted Through Double-Slits
Historical Aside
In 1801 Thomas Young devised a classic experiment for demonstrating the wave nature
of light similar to the one diagrammed in Figure 6.4. By passing a wide plane wave
through two slits he effectively created two separate sources that could interfere with
each other. (A plane wave is a wave consisting of parallel wave-fronts all traveling in
the same direction.)
For a given direction, θ, the intensity observed at point P on the screen will be a
111
CHAPTER 8: EXPERIMENT 6
R
y
x
Figure 8.2: A schematic diagram of our experiment showing how we can determine the
scattering angle, θ, by measuring the distance from the optical axis and the distance between
the slits and the screen.
superposition of the light originating from every slit. Whether the two waves add or cancel
at a particular point on the screen depends upon the relative phase between the waves at
that point. (The phase of a periodic function is the stage it is at along its periodic cycle;
the argument of the sine or cosine function is its phase.) The relative phase of the two
waves at the screen gradually increases as a function of direction causing periodic intensity
minima and maxima called fringes (see Figure 6.2). The spacing of the fringes depends on
the distance between the two slits and the wavelength of the light.
Equation (8.1) gives the intensity versus direction for each of the two slits; however,
interference occurs by the superposition of the two electric fields
E = E0
sin α
[sin(ωt − kx1 ) + sin(ωt − kx2 )]
α
(8.5)
where the two amplitudes are equal for a uniform plane wave incident upon two equal width
slits. As the observer moves around the mask with the two slits, x1 and x2 will vary. We
let the width of the two slits be a and the distance between the centers be d so that the
notation is consistent with previous developments. We place the origin of coordinates midway
between the slits so that x1 = x − d2 sin θ and x2 = x + d2 sin θ. We substitute this above into
Equation (8.5) and use a trigonometric identity sin A + sin B = 2 sin 12 (A + B) cos 21 (A − B)
to find
sin α
1
1
E = E0
sin ωt − kx + kd sin θ + sin ωt − kx − kd sin θ
α 2
2
sin α
1
1
= E0
2 sin (2ωt − 2kx) cos (kd sin θ)
α
2
2
sin α
1
= 2E0
cos (kd sin θ) sin (ωt − kx)
α
2
If we square this and average over a long time, the result becomes the intensity
sin α
I(θ) = I(0)
cos β
α
2
112
sin α
= I(0)
α
2
cos2 β
(8.6)
CHAPTER 8: EXPERIMENT 6
where
1
1
2π
πd
kd sin θ = · d ·
sin θ =
sin θ = β.
(8.7)
2
2
λ
λ
The average of sin2 ϕ is 21 and
the constants out front get
absorbed into I(0). From the
result in Equation (8.6) we see
that it is the simple product of
the single slit result in Equation (8.1) and the very narrow double-slit result in Equation (6.1). This combination is
illustrated graphically in Figure 8.3.
You will observe this intensity distribution in Part 2. We
will take data using the PIN
photodetector and treat the
intensity versus detector position graphically. We will see
if the model of Equation (8.6)
fits the data adequately and
whether it predicts the same
a and d that the mask’s manufacturer specified.
Figure 8.3: Graphical plots of light intensity for inIf the model satisfies these
terference, diffraction, and the combined effects for light
aspects
of your data, you will
transmitted through matched double slits.
have very strong evidence that
Huygen’s principle that was used in each individual slit to achieve the observed diffraction
is valid and that the superposition principle for electric and magnetic fields is valid.
A similar analysis for N equally spaced identical slits yields
sin α
I(θ) = I(0)
α
2
sin N β
N sin β
!2
.
(8.8)
This is very useful for predicting the detailed interaction of light with diffraction gratings.
8.2
The Apparatus
We will be using Pasco’s optical bench shown in Figure 8.4. Pasco’s laser diode module
fits their optical bench and will supply the coherent light for our experiment. The light
will illuminate Pasco’s slit set shown in Figure 6.5 and Figure 7.3 at normal incidence.
113
CHAPTER 8: EXPERIMENT 6
The resulting interference and diffraction patterns will then be detected by Pasco’s PIN
photodetector. The photodetector can be moved across the optical axis and its position can
be monitored by their rotary encoder and rack-and-piñon gear.
Pasco’s rotary encoder, CI-6538, reports the angle of its shaft and pulley rotation in
radians (rad). We would like to determine the detector’s perpendicular location, y, in meters
(m). After examining the rack-and-piñon gears carefully, we have determined that the piñon
gear has 24 teeth. The rack is threaded at 3 teeth/cm. As the encoder makes one revolution,
the computer will report 2π rad and the carriage will move the distance of 24 teeth. We can
then find the distance, y, that the carriage will move to be
y(ϕ) =
24 teeth
2π rad
3 teeth
0.01 m
×ϕ=
0.04 m
ϕ.
π rad
(8.9)
πy
and we
Additionally, both the slit width α and the separation β contain z = πλ sin θ ≈ λx
can choose to separate our slits from our screen by 1.000 m; so we can let Ga3 calculate a
(0.04 m)πϕ
πy
0.04 ϕ
column for z ≈ λx
= (1.000
= 670×10
−6 mm using
m)πλ
0.04 * “Phi” / (670 * 10^-6)
(You need to define “z” somewhere in your Procedures or Data so your reader will know the
meaning of your x-axis: z = πλ sin θ.) The units of z are “1/mm”; we will let this be our
horizontal axis and the light intensity be our vertical axis when we plot our data.
Figure 8.4: A photograph of the apparatus used to measure the intensity distribution of
our light patterns. The x and y axes are indicated as are the diode laser light source, the
slit pattern wheel, and the rotary encoder used to move the detector along the y-axis and to
measure its motion.
8.2.1
Part 1: Light Intensity Distribution for Single Slit
Configure Pasco’s Capstone program to gather your data. A suitable setup file can be
downloaded from the lab’s website at
http://groups.physics.northwestern.edu/lab/intensity.html
114
CHAPTER 8: EXPERIMENT 6
Measure the intensity distribution of the diffraction pattern generated by the narrowest
vertical slit on the detector shape wheel. Set your sample slits ‘exactly’ 1.000 m from your
detector shape wheel. Turn on your laser diode and verify that the reflection from the sample
pattern has the same horizontal (y-direction) position as the laser aperture. This assures
that the laser and slit pattern are very nearly perpendicular. It might be necessary to fold
up some scrap paper and to wedge it between the pattern wheel holder and the optical bench
track to obtain correct performance. Move the detector along the rack to one side of the
diffraction pattern where the pattern is very dim but visible in low light. Click “Monitor” at
the bottom left and very, VERY slowly turn the rotary encoder wheel at constant speed until
the detector passes through the diffraction pattern. As you turn the wheel, the computer
should plot your diffraction pattern on the graph. Click “Stop” at the bottom left.
Copy and paste your data into Vernier Software’s Ga3 graphical analysis program. A
suitable configuration file for Ga3 is also available for download from the website.
Plot the intensity on the y-axis and “z” on the x-axis.
Try to fit your data to the theoretical model in Equation (8.1). It would be wise to save
your data. Draw a box around your data points, Analyze/Curve Fit..., and select the “single
slit” model from the bottom of the list. Be sure the model agrees with
bg + I0 * (sin (a * (x-x0)) / (a * (x-x0)))^2
It might be necessary to fit manually until the model is fairly close to the data points. “bg” is
the vertical offset due to background room light and detector leakage due to thermal energy,
“I0” is the height of the central maximum, “x0” is the location of the central maximum on the
x-axis, and “a” is the width a of the single slit. Once the fit is fairly close, ‘Done’ to exit the
fitter and to replace the default parameters. Now activate the fitter again (Analyze/Curve
Fit...) and try to autofit.
Make sure you have uncertainties specified for your fit parameters. If not right-click the
parameters box, ‘Properties...’, and enable “Show Uncertainties”. If you need more significant
figures, change the parameters properties again to get more.
Calculate from your data the ratio I(θ)/I(0) for the first (m = 1), second (m = 2),
and possibly third (m = 3) subsidiary maxima. What are your measurement errors in these
ratios? Carry out your calculations for both peaks
√ corresponding to +m and −m, and give as
a result the average value. Divide your error by 2. Make sure you subtract the background
“bg” from all of your intensity measurements.
Predict these ratios using Equation (8.4). Keep enough significant digits so that your
roundoff error is significantly less than your measurement error above; now you can treat
these numbers as exact.
8.2.2
Part 2: Light Intensity Distribution for Double Slits
Now, observe the various intensity distributions for the available double-slit pattern masks.
Choose one for detailed analysis and repeat the procedure in Section 8.2.1 above except now
115
CHAPTER 8: EXPERIMENT 6
the fit function must describe the distribution for the “double-slit” sample pattern,
bg + I0 * (sin (a * (x-a0)) * cos (d * (x-d0)) / (a * (x-a0)))^2
In this case “a0” is the location of the envelope’s central maximum, “d0” is the horizontal
offset of the narrow fringes, and “d” is the distance d between the slits. The remaining
parameters are the same as for the single slit model.
8.3
Analysis
Our consideration of light waves interfering and diffracting led us to Equation (8.1) and
Equation (8.6). Try to imagine inventing these models without using wave interference;
how well do you imagine your model would fit your data? Keep your answers to these
questions in mind when you are deciding what your conclusions should be later. Before
we do that, however, our beautiful model spat out slit dimensions that we can compare
to measurements from the manufacturer obtained via other means. . . probably using a
microscope and micrometer scale. So a natural question is whether these two measurements
yield the same values for these respective dimensions. Surely by now we are all getting
familiar with the statistics needed to determine the answers to these questions.
Calculate the difference between the manufacturer specified single-slit width and the
measurement delivered by your model fitting
∆ = Fitted - Specified.
Calculate the error in this difference using
σ=
q
(δFitted)2 + (δSpecified)2 .
For each, is ∆ < σ? Is ∆ < 2 σ? Is ∆ > 3 σ? Recall that ∆ > σ about 1:3 and ∆ > 2 σ
about 1:22 just from random fluctuations; these probabilities are too large for us to assert
that the compared two numbers are not equal. But ∆ > 3 σ only 1:370 due only to random
fluctuations, so differences this large suggest that we conclude that the two numbers are
indeed different; statistics cannot tell us why, however. Repeat this quantitative analysis for
the single slit width, a1 , the double-slit width, a2 , and the double-slit separation, d2 . Also
analyze the measured peak height ratios with those predicted by Equation (8.4).
Can you think of anything in the experiments that might reasonably affect the measurements that we have not already included in our measurement errors? Discuss each of these
using complete sentences and paragraphs. In your view is it more likely that the theory
that has survived for a hundred years of professional tests is false or that you have made
some mistake or overlooked some significant sources of error that might explain your nonzero
difference(s)?
116
CHAPTER 8: EXPERIMENT 6
8.4
Conclusions
We are now ready to state simply and briefly what our data says about light. We have
already detailed the reasons why and should not repeat those reasons here; Conclusions
are merely a series of results that our data supports or contradicts clearly stated. Always
communicate with complete sentences to introduce valid equations (equations are equations
NOT sentences despite the fact that we tend to read them as though they were sentences)
and define the symbols (d, λ, θ, . . .) in the equations. We need not argue why we conclude as
we do at this point; however, we must state our conclusions clearly so that our reader can
understand them completely without reading anything else in our report.
Finally, report any measured quantities that we or other experimenters might find useful
in future work. If we expect that we might re-use our slit patterns, we might report their
measured dimensions. In each case communicate with complete sentences and include the
units and errors for the measurements.
8.4.1
References
Sections of this write up were taken from:
1. D. Halliday & R. Resnick, Physics Part 2, John Wiley & Sons.
2. R. Blum and D.E. Roller, Physics Volume 2, Electricity Magnetism and Light; HoldenDay.
3. E. Hecht/A. Zajac, Optics, Addison-Wesley Publishing Company.
117
CHAPTER 8: EXPERIMENT 6
8.5
APPENDIX:
The Semiconductor Diode Laser
Semiconductors are materials that can be pretty good electrical conductors in some situations
and pretty good insulators in other situations. The most widely used semiconductor material
is silicon (Si), but carbon (diamond) and germanium (Ge) have similar properties. Each
silicon atom in a solid crystal is bonded to four nearest neighbor silicon atoms. Since silicon
is in column IVA of the periodic table of the elements, this means that every atom is very
content with its bonding structure; every atom shares one electron covalently with each of
its four nearest neighbors and effectively has a full valence shell of eight electrons. All of the
electrons in the crystal are already busy holding the crystal together so that no electrons are
free to move about and to conduct electrical current. In solid state physics we say that an
energy gap has developed between the valence band and the conduction band, the valence
band is completely filled, and the conduction band is completely empty. Pure silicon is a
very good electrical insulator at low temperature and moderate electric fields. Pure silicon is
impossible to obtain, however, and no object has infinite volume so the surface atoms have
no nearest neighbors with which to share electrons.
If we imagine substituting a column IIIA atom like gallium (Ga) or boron (B) for one of
the atoms in the silicon crystal, we see that boron has only three electrons to share with its
four nearest neighbors. One of the boron atom’s neighbors wants another electron that boron
cannot give. It turns out that this “hole” (h+ ) can be filled by any one of the four shared
electrons near this hole moving into this position, but this leaves behind another hole. This
hole, in turn, can be filled by any of the four electrons near its position. If we consider that
the positively charged atomic nuclei are not moving along with their electrons, we will see
that the volume around the boron atom has become negatively charged and that the volume
around the hole has become positively charged. The negatively charged boron atom is fixed
in place by the crystal lattice, but the positively charged hole is now moving around inside the
material and conducting electrical charge. The addition of type IIIA elements to a silicon
lattice turns it into a conductor of positive charge. We call this “p-type” semiconductor
material. In solid state physics we say that the substitution of boron has added a hole to
the valence band. This is illustrated in Figure 8.5(a).
If we imagine substituting a type VA atom like phosphorous (P) or arsenic (As) for one
of the atoms in the silicon crystal, we see that arsenic has five electrons to share with its
four nearest neighbors. This leaves an extra electron (e− ) that is not needed to hold the
crystal together. This extra electron, then, is free to move around inside the solid and to
take its charge along with it. The arsenic nucleus, however, is fixed in place by the four
bonds to the lattice and when we removed one of its electrons the volume around the arsenic
core became positively charged. Similarly, the mobile volume around the extra electron is
negatively charged. This charge motion is an electrical current. The addition of type VA
atoms to a silicon crystal turns it into a conductor of negative charge. We call this “n-type”
semiconductor material. Figure 8.5(b) illustrates this situation. In solid state physics we say
that the substitution of arsenic has added electrons to the conduction band.
118
CHAPTER 8: EXPERIMENT 6
Figure 8.5: Two illustrations of how doping silicon can generate a conductor. In (a) a
boron (B) atom replaces a silicon (Si) atom and creates an electron vacancy or hole in the
valence band. In (b) an arsenic (As) atom replaces a Si atom and leaves an extra free electron
in the conduction band.
It is also possible to form semiconductors using molecules such as GaAs or InP instead
of atoms to build up the crystal. These binary III-V semiconductors are generally doped
by replacing their atoms with silicon; replacing the column III atoms with silicon yields
conduction electrons and replacing the column V atoms with silicon yields valence band holes.
Ternary semiconductors like GaAlAs also have properties different than other materials; we
can exploit specific properties of the various materials to build up the particular set of
properties we need for a particular device to have. Finally, there are organic semiconductors
that usually exploit a molecular substrate instead of a crystal lattice to obtain semiconductive
properties. This allows organic semiconductors to be very flexible instead of brittle like
silicon.
If we imagine building a semiconductor device by beginning with a p-type substrate and
adding layer after layer of n-type material, the result is a pn-junction. The converse process
of beginning with a n-type substrate and adding p-type layers also generates a pn-junction.
The second law of thermodynamics would suggest that the extra electrons diffuse from the
n-type material to fill the entire volume of the crystal uniformly with electrons. Similarly,
the holes should diffuse from the p-type material and fill the crystal uniformly with holes.
The crystal does, in fact, try to obey the second law of thermodynamics; however, electrons
and holes are each electrically charged so that a very large electric field develops in the
vicinity of the junction. As electrons moved into the junction, they left behind a positive
charge; similarly, holes left behind a negative charge. This makes a large electric field point
from the n-type material toward the p-type material as shown in Figure 8.6. Ordinarily,
this electric field would result in a large current but most of the electrons that enter the
junction recombine with the holes that enter the junction and become a silicon bond once
again. Sometimes a hole and an electron can form a metastable “exciton” wherein they
orbit each other like the electron and proton in the hydrogen atom. Once all of the charges
are thus immobilized in the junction region, the junction becomes a very good insulator
that cannot conduct electric current; the junction region has no free mobile charges so we
call it an “intrinsic” semiconductor. In photodetectors we intentionally add pure (intrinsic)
119
CHAPTER 8: EXPERIMENT 6
semiconductor material between the p and n materials to increase the likelihood of absorbing
a photon in this volume; this forms a p-type - intrinsic - n-type or pin-junction.
Figure 8.6: An illustration of charges flowing across a pn-junction. Most of the time the
electrons and holes simply recombine once again to become an immobile, neutral silicon bond.
Sometimes an electron and hole form a metastable exciton where they orbit each other like
the charges in a hydrogen atom. In (c) these processes are shown from the band theory of
solids perspective.
If we attach the positive terminal of a battery to the p-type material and the negative
terminal to the n-type material, current will flow. In fact, so much current will flow that if
we do not somehow limit the current, the device will quickly heat up and burn out. As the
battery helps cancel the electric field in the junction region, the electrons and holes enter the
junction as a battery current and recombine. Each time an electron-hole pair recombines
the energy of attraction between them is released as a photon. The energy of the photon is
. A pn-junction is a
equal to the band gap energy Eg of the semiconductor, Eg = hf = hc
λ
light emitting diode (LED) but the light is outside the human visible range (400-700 nm) for
most diodes. Gallium arsenide (GaAs) diodes emit the bright red light used in calculator
displays in the 1970s.
Over the years we have developed ways to trap the photons emitted by some pn-junctions
by making the surfaces around the junction region highly reflective. By containing the
light in this manner, we greatly increase the rate that these trapped photons stimulate
photon emissions and pair recombination. As we may have learned earlier in studying the
HeNe laser, these stimulated emissions have exactly the same energy (wavelength), direction
(momentum), and phase as the photon that stimulated the emission; the two photons are
coherent and have the same quantum state. Since photons satisfy Bose-Einstein statistics
instead of Fermi-Dirac statistics, it is not forbidden for many photons to have the same state.
These two photons are now twice as likely to stimulate another photon in their state as any
of the singlet photons in the device. Once one of them does stimulate another emission, the
three photons will be three times more likely to stimulate another like themselves, etc. Very
soon a very large fraction of the photons in the laser have the same wavelength, direction, and
phase. The light emitted by the semiconductor diode laser is coherent and monochromatic.
From this discussion one should not deduce that all semiconductor diode lasers are made
from silicon. In fact, only recently have we figured out how to make lasers from silicon at
120
CHAPTER 8: EXPERIMENT 6
all. Additionally, the color of the light is determined by the semiconductor’s energy gap;
since there are lasers having many different colors, they must be made from many different
semiconductors. Since the light wavelength is determined by the semiconductor’s band gap,
it is possible to tune the wavelength over a few dozen nanometers range by adjusting the
diode’s temperature. At higher temperature the crystal expands so that the atoms are
further apart and the attraction between them (the energy gap) is reduced slightly.
8.6
The PIN Diode Photodetector
When energetic particles irradiate a semiconductor, the resistivity of the semiconductor
decreases. The energetic particles break molecular bonds by colliding with the valence
electrons. Each broken bond yields an electron free to conduct electricity in the conduction
band; each broken bond also yields a free hole in the valence band and these increases in
free charge carriers increase the electric conductivity (σ = ρ1 ) and reduce the resistivity.
Eventually, these carriers reach the edge of the semiconductor or recombine with another
partner to recover the status quo when the irradiance is removed. This makes semiconductors
good photoconductors.
In order to generate an electron-hole pair, the incident particle must deposit enough energy upon the bound electron to break the chemical bond. This energy is the semiconductor’s
band gap energy, Eg . Very energetic particles might break several bonds each before running
out of energy; each collision costs the particle Eg so that counting the broken bonds can give
information about the energy of the incident particle. This property makes semiconductors
very valuable to high energy physicists.
Alternatively, if the energies of incident particles are known to be near the gap energy,
then counting the broken bonds yields information about the brightness or intensity of the
beam. In our discussion of the pn-junction above, we noted that electrons from the n-type
material diffuse across the junction as do holes from the p-type material to recombine and
to make several microns thickness of intrinsically pure semiconductor at the junction with a
high electric field.
When light with sufficiently high frequency encounters this junction, it breaks these
bonds. This high electric field then pushes the alleviated holes toward the p-type material and
the electrons toward the n-type material to generate a small potential difference between the
two sides of the pn-junction. Solar cells can generate electric power utilizing this photoelectric
effect, but pn-junctions also make sensitive and linear photodetectors. Since each photon
creates one electron-hole pair, the generated current is directly proportional to the light’s
intensity.
The biggest problem with pn-junction photodetectors is that such a thin junction absorbs
very few of the incident photons; most pass through without interacting with the junction.
To increase the junction’s thickness, we deposit a layer of intrinsically pure (i) material
between the p-type and the n-type materials. These pin-junctions (PIN diodes) are more
sensitive and have faster response than regular pn-junctions.
121
CHAPTER 8: EXPERIMENT 6
122
Chapter 9
Experiment 7:
Light Polarization
WARNING
This experiment will employ Class III(a) lasers as a coherent, monochromatic light
source. The student must read and understand the laser safety instructions on
page 89 before attending this week’s laboratory.
9.1
Introduction
We might recall that light is “transverse electro-magnetic waves”. James Clerk Maxwell’s
electrodynamics equations describe these waves in detail. Transverse waves have the E and
B vectors perpendicular to the direction of wave propagation. Out of 3-dimensional space,
this still leaves two dimensions (or two degrees of freedom) in which the vectors might point;
they can point in any radial direction around the light ‘rays’. These two degrees of freedom
are represented mathematically by two orthogonal coordinate axes.
These two coordinates are the basis for specifying the polarization of the light. The
electric field vector E can be specified completely using only these two coordinates. Although
the same is true for the magnetic field vector, the electrons in dielectrics get moved by the
electric field; they experience an electric force −eE. Since their velocities are much smaller
that light-speed, any magnetic force is much smaller and their random velocities generally
average to zero quickly anyway. (The positively charged nuclei are thousands of times heavier
than the electrons so that their response to the waves are neglected; their accelerations are
thousands of times less.)
This leads us to specify the polarization p̂ of the light to be the direction of the electric
field, E(t) = E(t) p̂. We also know that sinusoidal waves are equal parts positive and negative
so that there is no difference between positive and negative polarization, p̂ ⇔ −p̂. Linear
polarization has the polarization vector p̂ a fixed unit vector in space and time.
123
CHAPTER 9: EXPERIMENT 7
Figure 9.1: A polaroid absorbs oscillating electric fields parallel to its grain. This can
polarize natural light or it can check whether light is already polarized. Polarized light will
be absorbed when its electric field is parallel to the polaroid’s grain.
This is the most common form of polarization and the one we will be studying in this
lab. If the plane of vibration rotates around the direction of propagation, then the light
is said to be elliptically polarized. If the major and minor axes of an ellipse are equal,
the ellipse is a circle and the same is true for circularly polarized light. Depending on the
direction of rotation the light may be right- or left-circularly polarized. These two rotation
directions are also independent of each other and form an alternate basis for specifying a
general polarization.
An ordinary light source consists of a very large number of randomly oriented atomic
emitters. Each excited atom radiates a polarized wave train of roughly 10−8 s duration (in
other words imagine a sinusoidal wave about 3 m long). New wave trains are constantly
emitted and the overall polarization changes in a completely unpredictable fashion. These
wave trains make up natural light. It is also known as unpolarized light, but this is a bit of a
misnomer since, in actuality, every wave train is polarized but the wave trains’ polarization
planes are randomly oriented in space (i.e. are different polarization states). The set of all
wave trains has every possible polarization in equal abundance.
In this lab you will
1) study the phenomenon of light polarization,
2) compare our observations to Malus’ law and to Brewster’s law
3) learn about the function and use of a semiconductor diode laser, and
4) learn about the function and use of a PIN photodiode light detector.
The laser is described in the appendix following the writeup on page 118. You will be quizzed
on the material in the appendix as well as on the lab write up.
Light’s polarization can be used to manipulate light. Just as changing its wavelength
inside different dielectrics allows us to bend and to focus light, placing optical elements
124
CHAPTER 9: EXPERIMENT 7
Figure 9.2: A photograph of the light detector and shape wheel. We will use one of the
circular apertures.
between two polarizers allows us to choose whether the light passes the second polarizers.
For example, liquid crystals (nematic fluids) rotate the polarization of light so that we can
choose with an electric field whether the polarization matches the second polarizer and is
transmitted. Many materials exhibit electro-optical or magneto-optical effects that can also
be used in this manner. Birefringent (or dual index of refraction) crystals can be cut to
exactly the right length to form half-wave plates or quarter-wave plates whose orientation
relative to the incident polarization affects the polarization state of the transmitted light.
Finally, light reflected from dielectric surfaces is partially polarized. Light reflected at the
Brewster’s angle from a dielectric surface is completely polarized. We will observe the
Brewster’s angle for Lucite as part of today’s experiment.
Checkpoint
What property of electro-magnetic radiation determines its polarization?
Checkpoint
What is a wavetrain? What is the plane of vibration of light? What is the difference
between polarized and natural light?
125
CHAPTER 9: EXPERIMENT 7
Checkpoint
Is the light emitted by most light sources polarized? Explain. What is circularly
polarized light?
9.1.1
Polarizers
An optical device whose input is natural light and whose output is some form of polarized
light is known as a polarizer. We know a variety of ways to polarize light. All of these
techniques have in common some form of asymmetry associated with the way they operate.
Three such techniques are discussed next.
1. Wire-Gridiron Polarizer. Imagine that an unpolarized electromagnetic wave impinges
on a gridiron of very fine wire from the left. (See Figure 9.1.) The electric field can
be resolved into two orthogonal components; in this case, one chosen to be parallel to
the wires and the other perpendicular to them. The y-component of the field drives
the conduction electrons along the length of each wire, thus generating a current.
This current heats the wires so that energy is transferred from the field to the grid.
In contrast the electrons are not free to move very far in the x-direction and the
corresponding field component of the waves is essentially unaltered as it propagates
through the grid. The transmission axis of the grid is accordingly perpendicular to the
axes of the wires. The green arrows in Figure 9.1 indicate the polarization axis.
2. A Polaroid is a molecular analog to the wire gridiron. A sheet of clear polyvinyl
alcohol is heated and stretched in a single direction, its long hydrocarbon molecules
becoming aligned in the process. The sheet is then dipped into an ink solution rich
in iodine. The iodine impregnates the plastic and attaches to the straight long-chain
polymeric molecules, effectively forming a chain of its own. The conducting electrons
associated with the iodine can move along the chain as if they were long thin wires.
The component of E in an incident wave which is parallel to the molecules drives the
electrons, does work on them, and is strongly absorbed. The transmission axis of the
polarizer is therefore perpendicular to the direction in which the film was stretched.
3. A polarizing beam-splitter separates an incoming beam of light into a transmitted,
horizontally polarized beam and a reflected, vertically polarized beam. These polarizers
make use of Brewster’s law that will be studied today.
Checkpoint
How can you produce a beam of linearly polarized light? How can you establish if a
beam of light is linearly polarized? How does a polaroid film polarize a beam of light?
126
CHAPTER 9: EXPERIMENT 7
9.1.2
Malus’s Law
How do you determine experimentally whether or not a device is actually a linear polarizer? Consider
Figure 9.1 where natural (unpolarized) light is incident on an ideal
linear polarizer. Only light with
a specific orientation (polarization
state) will be transmitted. That
state will have an orientation parallel to a specific direction which
we call the transmission axis of the
polarizer. In Figure 9.1 the transmission axis is depicted by green
arrows. In other words, only the
component of the optical field parallel to the transmission axis will
pass through the device unaffected.
If the polarizer is rotated about the
z-axis the amount of transmitted
light will be unchanged because of
the complete symmetry of unpolarized light. Now suppose that we
introduce a second possibly identical ideal polarizer, or analyzer,
whose transmission axis is vertical.
If the amplitude of the electric field
transmitted by the polarizer is E0 , Figure 9.3: The polarization light perpendicular to
only its component parallel to the the plane of incidence is unaffected by reflections at
transmission axis of the analyzer dielectric surfaces.
will be passed on (assuming 100%
efficiency). This component will have magnitude E0 cos θ. The observed intensity is the
square of the amplitude, consequently
I(θ) = I0 cos2 θ.
(9.1)
This is known as Malus’s law, having first been published in 1809 by Etienne Malus,
military engineer and captain of the army of Napoleon. Observe that I(90◦ ) = 0. This arises
from the fact that the electric field that has passed through the polarizer is perpendicular
to the transmission axis of the analyzer (two devices so arranged are said to be “crossed”).
127
CHAPTER 9: EXPERIMENT 7
Checkpoint
What is the relation between polarizer orientation and transmitted light if the incident
light is linearly polarized?
Checkpoint
What happens to the polarization of light that doesn’t pass the polarizer?
Checkpoint
What is Malus’ law?
9.2
Part 1
Observe the polarization of
your laser beam. Rotate a polaroid
film placed in your laser beam, and
then look for changes in the beam
intensity on the screen (Figure 9.2).
The polaroid film has the same
function as the analyzer shown in
Figure 9.1. If the intensity of the
transmitted light does not change
when rotating the analyzer, the
beam is not linearly polarized. If
it varies according to Malus’s law
(Equation (9.1)) the light is linearly polarized. Enter your observations in your Data.
Observe the polarization states
of the light traversing a polaroid
film. As described before, light
transmitted through a polaroid
film is linearly polarized. Place
one polaroid film in the laser beam.
This will transmit linearly polarized light whether or not your laser
generates a polarized beam. This Figure 9.4: A sketch of a green light ray reflected by
film is the polarizer. Rotate the a dielectric surface. The polarization in the plane of
polarizer to get maximum trans- incidence is greatly reduced by the reflection.
128
CHAPTER 9: EXPERIMENT 7
mission (this will be 90◦ from minimum transmission). Now insert a second polaroid film (the
analyzer) downstream of the first one. For the analyzer choose the polaroid with the optical
encoder attached. Rotate the analyzer keeping the polarizer fixed. The intensity you observe
on the screen will then go through maxima and minima, as predicted by Equation (9.1).
When the transmission axis of polarizer and analyzer make an angle of 90◦ , no light will be
transmitted (analyzer and polarizer are crossed). Describe your observations in your Data.
Execute the Pasco Capstone configuration file from the lab’s website at
http://groups.physics.northwestern.edu/lab/polarization.html
Be sure the transmitted light enters the detector.
Click “Record” at the bottom left and slowly rotate
the analyzer at least one revolution. Be careful or the
analyzer will fall out of its housing. Click “Stop” at
the bottom left. Be careful not to disturb the laser or
the detector until experiment 1d) is complete. Click
one entry of the table, press ctrl+a to select all of the
table, and press ctrl+c to copy the table contents to
Window’s clipboard. Now execute Vernier Software’s
Ga3 graphical analysis program, click row 1 under the
angle header, and press ctrl+v to paste the data into
Ga3. Draw a box around the data points on the graph
and Analyze/Automatic Fit. Fit the transmitted
intensity to Malus’ law near the bottom of the list.
This model will fit your data using
Figure 9.5: A graphical plot illusb + I0 * (cos(x - x0))^2
trating how reflected light is polarized
differently for different angles of in- Verify that the formula is correct and “Try Fit”. If the
cidence.
model line passes through your data, click “Done” and
make sure the uncertainties in the fit parameters are
shown. Print your graph for your notebook and copy and paste it into your MS Word report.
Place a third polaroid film (use the polaroid with the encoder attached for the middle
one) between crossed polarizer and analyzer. The polarizer and analyzer are crossed when
(without the middle polarizer) no light is transmitted. When rotating this third (middle)
filter the transmitted intensity goes through a maximum which appears each time the filter in
the middle is rotated by 90◦ . Explain (briefly in your Data) what you are observing in terms
of the fact that an analyzing filter placed in a linearly polarized beam of light effectively
rotates the plane of polarization of the light to the axis of the polarizer and reduces the
intensity to the projected component. For which orientation of the transmission axis of the
filter in the middle do you observe a maximum or a minimum of transmitted light intensity?
Copy and paste this data into Gax as before. Fit this data to the “Malus 2” model near the
bottom of the list; this model should agree with
b + I0 * (sin(2 * x - x0))^2
129
CHAPTER 9: EXPERIMENT 7
Show analytically that the intensity of the transmitted light, in the configuration of
experiment 1c), will give maxima at intervals of 90◦ of the middle filter (Apply Malus’ law
each time linearly polarized light goes through a polarizing sheet and don’t forget your
trigonometry). If the detector or laser was inadvertently disturbed despite the warning,
repeat 1b) without disturbing the laser or detector. If only the middle polarizer is the
difference between 1c) and 1d), then the peak intensity of 1c) should be four times the peak
intensity of 1d). Unfortunately, even when the polarization is aligned with the polarization
axis of the polaroid only 76% ± 1% of the light passes. Polaroids are lossy polarizers so we
must compensate for the fact that in 1d) the light passed three polaroids and in 1c) the light
passed only two by dividing the intensity in 1d) by 0.76. Predict the intensity in 1c) using
the intensity in 1d),
4 I0
.
(9.2)
Ipredicted =
0.76
Combine the errors in the measured intensity with the error in the polarizer efficiency to
estimate the error in this prediction,
δIpredicted = Ipredicted
v
u
u
t
δI0
I0
!2
1
+
76
2
.
(9.3)
Checkpoint
What is the efficiency of our polarizers?
9.2.1
Polarization By Reflection
One of the most common ways to polarize light is to reflect the light off of some dielectric
medium. The glare spread across a window pane, a sheet of paper, or the sheen on the
surface of a telephone or a book jacket are all partially polarized. One simple, although
incomplete explanation of this polarization is supplied by the electron-oscillator model.
Consider an incoming plane wave linearly polarized so that its field is perpendicular
to the plane of incidence (see Figure 9.3). The wave is refracted at the interface entering
the medium. Its electric field drives the bound electrons, in this case normal to the plane
of incidence, and they in turn re-radiate a reflected component of the incident light. The
radiation emitted by an electron oscillating along a straight line is called dipole radiation.
Its electric field is largely parallel to the direction of motion of the charge and no radiation
is emitted along the axis of the dipole (the direction of oscillation). It is consequently clear
from the geometry of the dipole radiation pattern that both the reflected and refracted waves
must also be in the same polarization state as the incident radiation.
On the other hand, if the incoming field is in the incident plane as shown in Figure 9.4
the electron-oscillators near the surface will vibrate under the influence of the refracted wave.
130
CHAPTER 9: EXPERIMENT 7
The flux density of the reflected wave is relatively low because the reflected ray direction
makes a small angle ϕ with the dipole axis. If we could arrange things so that ϕ = 0, or
equivalently θrefl + θrefr = 90◦ , the reflected wave would vanish entirely.
Consider an incoming unpolarized wave represented by two
components, one polarized normal
to the incident plane and one in
the incident plane. Under these
circumstances only the component
normal to the incident plane, and
therefore parallel to the surface,
will be reflected. The particular
angle of incidence for which this
situation occurs is designated by θp
and is referred to as the polarization angle or Brewster’s angle, so
that θp + θrefr = 90◦ . Hence from
Snell’s law
n1 sin θp = n2 sin θrefr
(9.4)
Figure 9.6: A photograph of the Lucite block on the and from the fact that θrefr = 90◦ − θp
rotary table and the optical bench.
it follows that
n1 sin θp = n2 cos θp
and
tan θp =
n2
n1
(9.5)
(9.6)
This is known as Brewster’s law after the man who discovered it empirically about
forty years before light phenomena were described as electromagnetic waves. The degree of
polarization of unpolarized light reflected from Lucite (n2 /n1 = 1.5) is shown in Figure 9.5.
The reflected beam is 100% polarized at 56.2◦ .
Checkpoint
What is Brewster’s law?
Checkpoint
A certain reflected light beam satisfies Brewster’s law. In which plane is the light
polarized?
131
CHAPTER 9: EXPERIMENT 7
9.2.2
Part 2: Confirm Brewster’s Law
We want to check Brewster’s Law by observing the polarization of the light reflected off
the surface of a block of Lucite when the
angle of incidence is set at the Brewster’s
angle (for Lucite θp = 56.2◦ ).
Set the Lucite block on the rotary table
(Figure 9.6). Hold the rotary table at 0◦
while orienting the Lucite block perpendicular to the beam. The reflection will return
to the laser when this is the case. (See
Figure 9.7.) The surface off which you are
reflecting the laser beam must be vertical
and situated along a diameter of the rotary
table.
We need some horizontal polarization,
but the lasers are oriented to give vertically
polarized light. Place a polarizer between
the laser and the Lucite and orient its
polarization axis at 45◦ . Rotate the rotary
table by θ1 = 56.2◦ and measure the polarization of the reflected beam using a polaroid
filter as an analyzer. Is the reflected light
polarized? Record your observations in your
Data.
Place a second polarizer oriented horizontally between the first polarizer and the
Lucite. Vary the angle θ1 and determine
for which value of θ1 the reflected beam
has least intensity. The observed degree of Figure 9.7: A photograph of the Lucite block
polarization should vary as shown in Fig- aligned to θ1 = 0.0◦ incidence. The reflection
ure 9.5. Since the incident light is oppositely has the same horizontal location as the laser
polarized, the observed intensity should vary exit port. If the angle is not zero on the scale,
as 100% minus the degree of polarization. In subtract its value from the Brewster’s angle
this configuration we are using the reflection later.
as an analyzer instead of a polarizer. Once
the Brewster’s angle is found, vary the second polaroid (closest to the Lucite) to try to get the
reflected intensity to be exactly zero. Slowly increase the angle until the reflection vanishes
(see Figure 9.8.) and read the angle. Continue increasing the angle until the reflection is
visible, slowly decrease the angle until the reflection vanishes again and read the maximum
reasonable Brewster’s angle. Now carefully rotate the rotary table back to zero and verify
that the surface is still perpendicular to the beam; if it is not, measure the angle that does
132
CHAPTER 9: EXPERIMENT 7
Figure 9.8: Two photographs illustrating how to bracket Brewster’s angle. In the first the
reflection is to the right of Brewster’s angle; rotate to the left until the reflection vanishes and
measure the angle. In the second the reflection is too far left; rotate right until the reflection
vanishes and measure the angle again. This gives estimates of Brewster’s angle and its error.
make it perpendicular and subtract this adjusted zero from your measurement of Brewster’s
angle. (Remember to keep the correct sign.) Remember to include the units and error with
your measurement.
Enter in your Data a brief description of what you have observed. Make a drawing. Using
your measured Brewster’s angle (corrected for zero) calculate the index of refraction of your
Lucite block. Remember that the index of refraction for air is very nearly 1.
133
CHAPTER 9: EXPERIMENT 7
Checkpoint
Polarization by reflection determines the plane of polarization. Is it the vertical or the
horizontal plane in which the vector of the reflected light oscillates? Explain.
9.3
Analysis
Is the peak intensity of the first graph four times the peak intensity of the second graph?
Is your measurement of Lucite’s index of refraction consistent with previous measurements
(1.495)? Investigate these questions by computing the difference and then comparing the
difference to your net error
∆ = n − 1.495
What other sources of error did you notice while performing your experiments? How
might each of these have affected your data? Do your models fit your data? Don’t forget
that the period of the sine (cosine) function was predicted explicitly by the model and was
not varied by the fitter.
9.4
Conclusions
What has your data demonstrated? Is Malus’ law supported? Contradicted? Is Brewster’s
law supported? Contradicted? Define all symbols used in equations and communicate with
complete sentences.
Have you measured anything that might be of value in the future? If so state your
measured values, units, and errors.
9.4.1
References
Sections of this write up were taken from:
• D. Halliday & R. Resnick, Physics Part 2, John Wiley & Sons.
• R. Blum and D.E. Roller, Physics Volume 2, Electricity Magnetism and Light, Holden-
Day.
• E. Hecht/A. Zajac; Optics, Addison-Wesley Publishing Company.
134
Chapter 10
Experiment 8:
The Spectral Nature of Light
10.1
Introduction: The Bohr Hydrogen Atom
Historical Aside
The 19th century was a golden age of science. We could explain everything we observed.
Near the turn of the century that began to change. The arrival of the microscope
allowed us to see random motion of wheat grains. Light emitted from hot objects had
spectrum different than expected; indeed the expected spectrum was unreasonable.
Light emitted or absorbed by atomic gases had sharp lines instead of continuity.
In this lab we will resolve some of the reasons for the confusion surrounding the state of
science in nineteen hundred. These explanations involve accepting that light has a particle or
quantum nature as well as the wave nature that our interference experiments have verified.
These explanations involve an atomic nature for materials instead of the continuous, two
charged fluid model suggested by Benjamin Franklin. These explanations even involve stable
quantum states in atoms where the accelerating electron does not radiate EM waves as
expected.
An atom has a diameter of about 10−10 m and is made up of a small (about 10−14 m),
heavy, and positively charged nucleus, surrounded by orbiting electrons. The nucleus consists
of protons (positive electric charge) and neutrons (no electric charge) bound together by
nuclear forces.
In a neutral atom there are as many negatively charged electrons as there are protons.
Each electron occupies one of the many possible well defined atomic orbit states. Each
particular orbit state has an associated total energy (kinetic + potential). Electrons “jumping” from one orbit with less energy to one with more (binding) energy will release discrete
quantities of energy in the form of light. The spectrum of quantized frequencies observed
in the light emitted by excited atoms is a direct measurement of the allowed transitions of
135
CHAPTER 10: EXPERIMENT 8
-e
me
e
M
r
Figure 10.1: Schematic force diagram for the nucleus and electron in a hydrogen atom.
electrons among different orbits in the atom. The emission spectrum of a given atom is a
unique signature of this atom. Even different isotopes in an element family have different
spectra.
Although the existence of discrete line spectra emitted by atoms had been known for a
long time, it was Niels Bohr who first calculated the spectrum of the hydrogen atom. This is
the simplest atomic system and consists of one proton as nucleus and one orbiting electron.
The electron describes a circular orbit in the electric field of the proton; the force acting on
the electron is
v2
e2
= Fe = −me ar = −me .
(10.1)
−
4πε0 r2
r
From Equation (10.1) the kinetic energy of the electron is
1
e2
2
KE = me v =
.
2
8πε0 r
(10.2)
The electrostatic potential due to the proton’s positive charge at a distance r is
V =
e
4πε0 r
(10.3)
and the potential energy, Ue = (−e)V of the electron is
Ue = −
e2
= −2KE
4πε0 r
136
(10.4)
CHAPTER 10: EXPERIMENT 8
Series Limit
Hydrogen Energy Levels
0
Series Limit
-1
-2
Series Limit
The total energy of the electron-proton system (of the atom) is
E = KE + Ue = KE − 2KE
e2
(10.5)
=−
8πε0 r
Brackett
Series
Paschen
Series
Bohr quantized the value of r by
postulating that the electronic orbit
must be a standing wave with wavelength λ, consequently the length of the
circle describing the electron’s trajectory must be the product of an integer
and λ,
2πrn = nλ
(10.6)
-3
Balmer
Series
-4
-6
-7
-8
Series Limit
Energy (eV)
-5
-9
where n = 1, 2, 3, . . .
-10
-11
-12
-13
Lyman
Series
-14
Figure 10.2: This figure shows an energy level
diagram for hydrogen along with some of the possible transitions. An infinite number of energy levels
are crowded between n = 6 and the escape energy
n = ∞.
The French physicist Louis de
Broglie postulated that one can assign
a wavelength λ to any object having
a momentum so that for the electron
p = me v; λ = hp = mhe v , where h is
Planck’s constant. Combining this with
Equation‘(10.6) we see that
2π rn = nλ =
nh
.
me v
(10.7)
We eliminate the electron’s velocity
from Equation (10.2) and Equation (10.7) to find
e2
1
1
nh
= me v 2 = me
8πε0 r
2
2
2π me r
and
1
e
=
r
nh
2
π me
.
ε0
!2
(nh)2
= 2
8π me r2
(10.8)
(10.9)
Checkpoint
What did Bohr postulate in calculating the energy spectrum of the hydrogen atom?
137
CHAPTER 10: EXPERIMENT 8
Table 10.1: Details about the photon interactions with hydrogen atoms for several ‘lines’.
Most humans can see the first 3-4 Balmer lines.
Checkpoint
What does quantization mean? Name five quantities that are quantized in nature.
Now we substitute this into Equation (10.5) to determine the atom’s energy to be
e2
e2
=−
En = −
8πε0 rn
8πε0
e
nh
2
π me
me
=−
ε0
2
e2
2 hε0
!2
1
1
=
−R
y
n2
n2
(10.10)
where the Rydberg constant is defined to be
me
Ry =
2
e2
2 hε0
!2
= 13.605 eV.
(10.11)
The radius rn of the orbiting electron and the binding energy En are quantized; they can
assume only discrete values! The quantity n is called the principal quantum number. The
138
CHAPTER 10: EXPERIMENT 8
Figure 10.3: The spectrum of white light as viewed using a grating instrument like the
one in this experiment. The different orders identified by the order number m, are shown
separated vertically for clarity. In actuality they would overlap.
radius rn increases as n2 . The energy values are negative because we are calculating a
binding energy; (one must supply energy in order to achieve an isolated electron and an
isolated proton at rest). Figure 10.2 shows the energy of stationary state and their associated
quantum numbers. The upper level marked n = ∞, corresponds to a state in which the
electron is completely removed from the atom; the atom is ionized.
Checkpoint
Why does the binding energy of an atomic electron have a negative value?
An atom radiates when, after being excited, it makes a transition from one state with
the principle quantum number n, and consequently with energy En , to a state m with lower
energy Em . The quantum energy carried by the photon is
hν = Eγ = En − Em = −Ry
1
1
−
.
n2 m2
(10.12)
The wave speed, the wavelength, and the frequency of oscillation are related by c = λν, so
we can find the wavelength of the emitted photon to be
λ=
c
hc
=
.
ν
Eγ
(10.13)
In our experiment we will wish to measure values for the Rydberg constant using our
139
CHAPTER 10: EXPERIMENT 8
Figure 10.4: A sketch of our grating spectrometer. Our gas is ionized to provide the source
of light. Lens A collimates the light into a beam the size of the grating. Lens B focuses the
light onto the cross-hair (see inset) and the eyepiece allows us to see the spectral lines. The
Vernier angular scale allows us to determine the wavelength of the line at the cross-hair.
measured wavelengths,
Ry = − hν
1
n2
−
1
m2
hc
=− 1
λ n2 −
1
m2
=−
1239.84 eV · nm
λ
1
n2
−
1
m2
.
(10.14)
We must keep in mind that Bohr’s
model above applies only to hydrogen and
to hydrogen-like atoms. To understand
more complex atoms we must incorporate
the revolutionary theory of quantum mechanics. Even quantum mechanics applied
to these complex systems cannot be solved
exactly, but we have developed approximate
solutions that agree quite well with experiment. Additionally, quantum mechanics can
explain the subtle variations in hydrogen’s Figure 10.5: A sketch of the apparatus (side
spectrum that are visible in the data you view) illustrating how to view the spectrum of
a hot tungsten filament.
will gather today.
140
CHAPTER 10: EXPERIMENT 8
The Grating Spectrometer
As already discussed in the second laboratory, gratings are used to analyze the frequency
spectrum of light. Light of a given wavelength, λ, will be deflected by a grating with a line
spacing constant d, by an angle θ, according to the relation
mλ = d sin θ with m = 0, 1, 2, . . .
(10.15)
where m is the order number.
Figure 10.3 shows how a grating spectrometer diffracts visible light in groups of intensity
distributions as a function of θ, and each of these groups corresponds to a different order
m. Previously, our experience with diffraction gratings was limited to illumination by
monochromatic lasers and we saw the spots into which the laser was diffracted. Previously
we saw spots because we were using only one color (or wavelength, λ) of light. Today, we
are illuminating the gratings with many colors simultaneously and each color will excite
every order of the gratings. Because of this it is important that we not allow ourselves to
become overwhelmed by what the spectrometer does with our light. Adjacent distributions
do overlap at the larger orders; third order violet occurs before second order red.
Figure 10.4 shows the spectrometer used for this experiment. It consists of a circular table
with a diffraction grating at its center and an angular Vernier scale along its circumference.
Two pipes are mounted on the table to keep out room light and these pipes intersect in the
region of the grating. The mounting of the first pipe is permanent. It is designed to carry
parallel light from an external source to shine upon the grating.
The second pipe is mounted in such a way as to be able to pivot about the center of
the circular table. This rotation makes it possible to separate the light, collecting only what
has been diffracted through some chosen angel, θ. If this pipe is set to an angle such as
θ = 10◦ , then whatever light the grating diffracts through an angle of 10◦ will travel down
the length of the pipe. It will be focused by the adjustable lens (B) and the eyepiece. A pair
of cross-hairs identify the center of the pipe and, together with the vernier scale located on
the equipment, allow the accurate measurement of the angle, θ.
The grating constant d is engraved on the frame holding the grating. Slit S, in Figure 10.4
defines the light source; the slit is parallel to the lines of the grating so the diffracted light
will form vertical lines instead of spots. Lens A is separated from the slit by a distance
equal to its focal length, f , and consequently it projects a beam of parallel light on to the
grating. Such a collimated beam utilizes most of the grating so that the spectra are quite
sharp. Lens B focuses the light diffracted by the grating into a focal plane which contains
the cross-hair. Both positions of lens B and the cross-hair can be adjusted in order to focus
the image better.
141
CHAPTER 10: EXPERIMENT 8
Checkpoint
Draw the path of two parallel light rays diverging from the spectrometer slit and
entering the observer’s eye.
Checkpoint
What is the physical significance of the order m of the spectrum produced by a grating?
The optics of the human eye is shown
schematically in Figure 10.6. The optimum focal distance of our eyes is about
25 cm. In order to observe an image at
a closer distance, a lens called an eyepiece
may be used as indicated in Figure 10.7.
The spectrometer has an eyepiece with focal
length of 2.5 cm. Each student will have
to adjust the position of the of lens B to
see a sharp image the spectral fringe. The
placement of the cross-hairs should then
be adjusted so that the two are in focus.
A small light bulb controlled by a pushbutton switch allows the cross-hairs to be
illuminated. To determine the axis (θ = 0)
Figure 10.6: Focusing system of the eye. of the spectrometer, place the table light
Most of the refraction occurs at the first sur- in front of the spectrometer slit, S, remove
face, where the cornea C separates a liquid the diffraction grating and look through the
with index of refraction n1 from the air. The pivoting arm of the spectrometer directly
lens L, which has a refractive index varying at the light source. Adjust the position of
from 1.42 in the center to 1.37 at the edge, the slit, of lens B, and of the cross-hair in
is focused by tension at the edges. The main order to see a sharp, white image (order
volume contains a jelly like ‘vitreous humour’ m = 0). When a sharp vertical image of
(n = 1.34). The image is formed on the the slit is centered on the cross-hair, you can
retina. Illumination levels are controlled by read the angle corresponding to the axis of
the aperture of the iris.
the spectrometer; use the Vernier scale as
shown in the appendix. All measurements
of θ that you will make must be with respect to the spectrometer axis so subtract this θ0
from all remaining angle measurements. Ga3 can do this for you if you simply incorporate
the subtraction into the column formula. Don’t forget to record the units and experimental
error for your measurements.
142
CHAPTER 10: EXPERIMENT 8
The Light Sources
In this laboratory you will observe the spectrum of four gases: H, He, Ne, and Hg. The
light source consists of a glass tube which
contains one of these gases at a pressure of
about 20-30 cm Hg. A 60 Hz voltage of a few
kilovolts is applied across the gas in the tube
via electrodes at each end. The non-uniform
electric field between the two electrodes will Figure 10.7: Simple lens used as a magnifier.
An object at O close to the eye can be focused
excite the gas in the tube.
by the eye to appear to be much larger and at
An electron will remain in an excited
a more distant point O’.
state for a time on the order of 10−8 s before
jumping down to a state with higher binding energy. The excited state, with a lifetime
τ ∼ 10−8 s, has then decayed into a lower energy state. In order to prolong the usefulness of
these tubes do not keep the light source on any longer than necessary.
Checkpoint
How might you excite an atom and how long does it stay excited?
10.1.1
Part 1: The Spectrum of White Light
The electromagnetic spectrum emitted by
the hot filament of the table light is a
continuous spectrum whose relative intensity depends upon its temperature. The
shape of the spectrum of a black body is
shown in Figure 10.9. It was Planck who
first calculated the shape of this spectrum.
Planck introduced a constant h, now known
as Planck’s constant, to reproduce mathematically the observed distribution of this
spectrum.
Observe the visible part of the electromagnetic spectrum emitted by your incandescent lamp. Look at the spectrum Figure 10.8: A sketch of the apparatus (side
associated with the order numbers m = view) illustrating how to view the spectrum of
0, 1, and 2. Observe the different colors as- an ionized gas.
sociated with different frequencies or wavelengths.
143
CHAPTER 10: EXPERIMENT 8
14000
12000
Watts/(m2 nm)
10000
Planck
Law
T=5000 K
8000
Rayleigh-Jeans
Law
T=3000 K
6000
4000
Planck
Law
T=4000 K
2000
Planck Law, T=3000 K
0
0
0.5
1
1.5
2
2.5
3
Wavelength (microns)
Figure 10.9: Blackbody Radiation Spectrum. Planck’s energy density of blackbody radiation
at various temperatures as a function of wavelength. Note that the wavelength at which the
curve is a maximum decreases with temperature.
Measure the spectral sensitivity of your eye by observing the highest frequency your eye
can discern. Use the order m = 1 to make these measurements. Measure the angle θ with
respect to the spectrometer axis (don’t forget to subtract off θ0 ) and use Equation (10.15)
to calculate the corresponding λ. Don’t forget your units and errors. Now measure the
lowest frequency your eye can see using the same method. Note the characteristics of the
filament’s spectrum in your Data. Are there holes in the spectrum or is it continuous?
Humans can see 400 nm < λ < 700 nm so be sure your measured wavelengths are reasonable
before continuing. Once you understand how to use the spectrometer, double-check your
knowledge by repeating the exercise on the other side of zero (for m = −1).
10.1.2
Part 2: The Hydrogen Spectrum
Start Vernier Software’s Ga3 graphical analysis program. A suitable Ga3 configuration file
can be downloaded from the lab’s website at
http://groups.physics.northwestern.edu/lab/spectral.html
The wavelength is calculated as you enter the order m and the diffracted angle θ using
Equation (10.15) λ = md sin θ; since the grating specifies lines/inch, this becomes
144
CHAPTER 10: EXPERIMENT 8
2.54 * 10^7 * sin(“Angle” - θ0 ) / (lines * “Order”)
in Ga3’s calculation equation. Another calculated column “Rydberg” with units “eV” and
formula
1239.84 / (“Wavelength” * (1/4 - 1/“Upper”^2))
is the Rydberg constant and is plotted on the y-axis. Equation (10.14) has been used as
this column’s equation. Use the controls at the bottom left to tell Ga3 about your θ0 and
lines/inch.
Observe and record as many spectral lines as you can see in the spectrum of hydrogen,
using a hydrogen gas tube. Make sure that the light source is properly aligned with the
spectrometer slit. At 0◦ the red and blue will merge into a bright sort of tan at proper
alignment (the same color as the directly viewed hydrogen tube). Hold the table as you
move the eyepiece or you will mess up your careful alignment and need to repeat it before
continuing. Enter the angle into Ga3 (θ), the diffraction order (m), and the upper electron
shell’s principal quantum number (red⇒ n = 3, cyan⇒ n = 4, violet⇒ n = 5). Compare
the wavelength of the lines you observe with the value shown in Table 10.1. Which series of
lines do you observe? Table 10.1 also gives the principal quantum numbers involved in the
observed transitions.
Hints for measuring the wavelengths of spectral lines:
1. Align and center the light source to make the lines as bright as possible.
2. Optimize the focus for each measurement using lens B. Make sure the diffraction grating
is aligned perpendicular to the incident, collimated beam (a peg on the slide’s bottom
should fit into a groove on the mount.)
3. Measure each color using all visible orders on both sides of the optical axis. Each order
yields a measured value of the Rydberg constant. Note correlations between Rydberg
constants gathered using one color and contrast these with constants gathered using
other colors.
4. Use some intuition in matching the measured wavelengths to the chart of known lines.
Even with careful measurement procedures your measured wavelengths may easily vary
as much as a couple dozen nanometers from those in the chart. Also the chart only
lists the brighter lines; other dim lines may also be present.
Checkpoint
Which one of the hydrogen series describes light in the visible spectrum?
145
CHAPTER 10: EXPERIMENT 8
Table 10.2: Several known lines for helium (He), neon (Ne), and mercury (Hg). These
may be used to identify these substances in chemicals when they are burned in a flame.
Checkpoint
What is the difference between the electromagnetic spectrum produced by an
incandescent object and the spectrum generated by excited atoms?
10.1.3
Part 3: The Spectrum of He, Ne, and Hg
The He gas tube is labeled while the tubes with Ne and Hg are only marked with colored tape.
Record the wavelength of 5 to 10 spectral lines of each one of these elements. Measure these
wavelengths only once each rather than once for each visible order and note their units and
errors. Notice that the spectrum of these gases is much more complicated, with many more
lines than the one of hydrogen. This is due to the larger number of electrons orbiting the
nuclei of these elements, the large number of electron-electron interactions, and consequently
the larger number of possible transitions corresponding to spectral lines. Table 10.2 gives the
wavelengths and the relative intensity of the line spectra of these elements. By comparing
your observed values with those on the table you will be able to tell which gas is enclosed in
a tube marked with a given color. Chemists find the spectroscopic uniqueness of atoms and
molecules quite useful in identifying unknown substances.
146
CHAPTER 10: EXPERIMENT 8
10.2
Analysis
Discuss your graph of measured Rydberg energies. It might help to rescale your y-axis from
0 to 15 eV. What trends do you see in the graph? Bohr’s model and quantum mechanics
predicts that all of the Rydberg constants are the same; is it conceivable that your data
agrees with this within your errors? If so, it makes sense to compute the average Ry and
standard deviation sRy using Analyze/Statistics. First, though, you will need to delete any
unused rows at the bottom of your table and to draw a box around your data points on your
graph. Move the parameters box away from your data so your readers can see every data
point. Print the whole screen for each member of your group and find the standard error in
your Rydberg constant
sRy
σ = sRy = √ .
N
Now, find the difference between your mean and the best measurement of others
∆ = Ry − 13.605 eV.
The standard error is the best estimate of the error in the mean, Ry = (Ry ± sRy ). Does your
Rydberg constant agree with everyone else’s? Disagree? How well do you know? What do
you observe about the environment of the hydrogen atoms that might affect the electrons’
energies? What does this all mean versus Bohr’s model?
Now discuss the three more complex spectra. Take a few minutes and try to fit helium’s
spectrum to Bohr’s model (Equation (10.10)). Do all of the lines fit or do we need a better
theory? Does it seem like we might have better luck with neon or mercury?
10.3
Conclusions
Is blackbody radiation characteristically the same or different than gas discharge light? Is
Bohr’s model valid? Under what circumstances? Did you measure anything that you and/or
others might find of value in the future? Remember to communicate using complete sentences
and to define all symbols used in equations.
10.3.1
Reference
Sections of this write up were taken from:
Bruno Gobi, Physics Laboratory: Third Quarter, Northwestern University
147
CHAPTER 10: EXPERIMENT 8
10.4
APPENDIX: The Vernier Principle
A vernier consists of a movable scale next to a stationary scale. The movable scale is marked
off in divisions that are slightly smaller than the divisions on the main scale. If you line up
the zero mark of the vernier with the zero mark of the fixed scale (see Figure 10.10), you will
notice that not all of the other divisions are aligned. However, if you examine the two scales
closely, you should observe that the nth division of the movable scale exactly coincides with
the n − 1 division of the fixed scale. This implies that n − 1 divisions of the main scale has
or 1 − n1
the same length as n divisions on the vernier scale; so each vernier division is n−1
n
times the length of a main scale division. Determining the quantity n1 is an important first
step in making any measurement with a vernier; n1 is called the “least count”.
The least count gives an indication of the precision of the particular measuring device. For example,
if we can read the main scale of
our device to the nearest degree,
and the device has a least count
of 1/4 (i.e. 4 vernier divisions is
equal in length to 3 main scale
divisions) then we can make meaFigure 10.10: An illustration of the Vernier scale. surements with an instrumentally
The position of the movable 0 indicates the coarse limited error of ± 1/4 of a degree.
reading on the fixed scale. One additional digit of Examine Figure 10.10. What is
precision can be obtained accurately from the Movable n? What is the least count of this
Scale digit that aligns best with a Fixed Scale number. Vernier scale? If each division of
the main scale corresponds to the
one degree, what is the precision of the measurements we can make with this device? A
well-designed instrument will have accuracy approximately equal to precision; the ability
to provide faithful measurements (accuracy) should be about the same as the amount of
information conveyed in a reading (precision). An instrument with too few displayed digits
defaults to having round-off be its greatest experimental error. Contrarily, having too
many displayed digits wastes money on useless precision and implies an accuracy which
it is incapable of providing. Keeping this in mind, we should expect that the experimental
error associated with an instrument is usually about the same as one or two least significant
digits of its carefully read display. In the case of our spectrometers, we should expect 0.1◦
errors in our angle measurements with reasonable care and attention to detail.
To read a measurement from a vernier such as the one in Figure 10.11, follow these steps:
1. Determine the least count of your device.
2. Look opposite the zero mark of the movable scale and read off what division of the
fixed scale is at the zero mark. If the zero mark does not exactly align and is situated
between two divisions, then read off the value of the lower of these two divisions. In
Figure 10.11, we read 46 degrees.
148
CHAPTER 10: EXPERIMENT 8
3. Examine each mark along the movable scale and determine which division (from zero
to n) is aligned exactly with a division of the main scale. Read off this number from
the movable scale. In Figure 10.11, we can see that 3 on the movable scale is aligned
with a division on the main scale. So we must add 3 least counts of 3/10 of a degree to
the number read from the main scale earlier, 46. Thus our final answer is 46.3 degrees.
If the zero mark (and simultaneously the n mark) of the movable scale had exactly
coincided with a division of the main scale, as in Figure 10.10, then we would add zero
least counts and arrive at an answer of 0.0 degrees.
Figure 10.11: An example tutorial in reading the Vernier scale. The movable 0 is between
the fixed 46 − 47, so the reading is 46.x. The x is determined by noting that the movable 3
matches the Fixed Scale numbers best (49 in this case); this makes x = 3 and our reading is
46.3. We might also note that the movable 0 is indeed quite close to 46.3 to double-check our
result.
Incidentally, all of the above is brought to you courtesy of Pierre Vernier (1585-1638),
a French engineer who spent most of his life building fortifications, but who designed the
Vernier scale in about 1630.
149
CHAPTER 10: EXPERIMENT 8
150
Appendix A
Physical Units
In science, we describe processes in Nature using mathematics. Math is very concise,
structured, and adaptable so that once we have mathematical models that mimic Nature, we
can make very specific and accurate predictions about what will happen in other situations.
Engineers use this fact to very good effect to obtain useful results in society.
Physical laws are usually expressed in terms of physical quantities that have dimensions.
The definition of units that are used to describe these dimensions is the raison d’être of the
National Institute of Standards and Technology (NIST). An example that we all should have
seen by now is Newton’s second law,
F(a) = ma
(A.1)
Given a mass whose “value” is m, to get motion whose acceleration is a we must apply a
push or a pull whose “value” is F. Since a push or a pull is an entirely different entity than
a mass, we include in F a different multiplicative variable (N, dyne, pounds, etc.) than we
include in m’s value (kg, g, slugs, etc.). The specific point that we need to address now is
“What about the parameter a?” What intrinsic multiplicative variable should we include
in a’s “value” so that the model is mathematically self-consistent? We can use algebra to
figure this out.
Let the unknown units be x and consider the specific case of F = 1 N and m = 1 kg . To
solve our problem we substitute these values into the model and solve for our unknown, x,
1 N = F = ma = (1 kg)(1 x) so x =
N
kg
(A.2)
If we multiply all of a’s pure numbers by the units N/kg , then the unknowns (and unknowables) that we call units will always cancel in such a way that forces will always have units N,
masses will always have units kg, and accelerations will always have units N/kg. Because all
of these are always true, our model is mathematically self-consistent. Of course, kinematics
has taught us that N/kg = m/s2 and that we can also determine acceleration by measuring
the distances that objects move, the rates that objects move, and the times needed for these
motions and rates to occur. One of the most beautiful and compelling aspects of physics is
the frequency that a single physical entity (acceleration in this case) can be determined in
151
APPENDIX A: Physical Units
more than one way (sometimes many, many more than one).
Let us now move on to a more general case. Let us pretend that we have developed a
model represented by
f (x) = ax + bx3
(A.3)
Without more information the units of f , x, a, and b are ambiguous; so, let us stipulate that
f is force (N) and that x is position (m). Is this enough information for us to determine
the units of a and b? Our first instinct might be to answer that “No, one equation cannot
yield two unknowns”; however, the rules of algebra must be obeyed as well. When we add
the two quantities ax and bx3 , they must have the same units. Furthermore, these common
units will be assigned to f , so the results of these multiplications had better yield units of
N! Now our problem has reduced to exactly the same problem as we solved above; we just
have to solve it twice in the present case. Let A be the units of a, let B be the units of b,
and substitute into the model:
kg
N
= 2
m
s
N
kg
so B = 3 = 2 2
m
s m
1 N = f = ax = (1 A)(1 m) so A =
1 N = f = bx3 = (1 B)(1 m)3
(A.4)
(A.5)
Models having any number of terms can be handled in exactly this same way; we just have to
solve the problem once for each term as above. Most students will also soon find short-cuts
that will make this much more expedient than it may seem just now.
Converting units
Before looking at more complex situations, we will summarize how to convert between
different physical units. Over the years many, many systems of units have been conceived
and used for specifying distance. Historically, it has been important for economic, political,
legal, personal, and scientific reasons that we have the ability to specify distance concisely
and accurately. From a need to know our height or shoe size to a need to know the area
of a land tract or to know how far away is the center of government, we need the ability to
measure and to communicate distances. The problem is that different purposes benefit from
somewhat different units of measure. It does not make sense to measure the distance to Los
Angeles in human hair-widths, for example, even though you often hear small things being
referred to “the thickness of a human hair” (∼ 100 micrometers, by the way). To compare
‘apples’ to ‘apples’, we invariably have to convert between different units of measure.
The simplest strategy to convert between systems of units is to place the unit for distance
in one system beside the unit for distance in the other system and simply to see how they
compare. We use one of the “yardsticks” to measure the length of the other “yardstick”. As
an example, we might use a meter stick to measure the length of a foot long ruler; when
we do so we will find that 1 ft = 0.3048 m. We could also use the foot ruler to measure the
meter stick and to find that 1 m = 3.2808 ft. Of course, these numbers are inverses of each
152
APPENDIX A: Physical Units
other, which is required for the measurements to be consistent. This implies that
0.3048
ft
m
= 1 = 3.2808
ft
m
(A.6)
Let us suppose that we are given some distance d = 33.24 ft and that we need to communicate
this distance to Paris, France, where no one has heard of “ft”; over there everyone measures
distance in “m”. We can multiply anything by 1 without changing its value. This applies to
d as well. We see that 1 = 0.3048 m/ft so that multiplying by 0.3048 m/ft is just multiplying
by 1.
m
d = 33.24 ft = 33.24 ft × 1 = 33.24 ft × 0.3048 = 10.13 m
(A.7)
ft
Dimensionless Functions
Frequently we find expressions like
f (x) = f0 eax or g(x) = g0 ln
x
x0
(A.8)
These functions belong to the class of exponential functions (recall that y = ex if and only
if x = ln y). What must the units of f0 , a, g0 , and x0 be in order that f and g be force (N)
and that x be distance (m)? First, realize that e ≈ 2.7183 is just a number, no different
than 3, 8, or 1 as far as units are concerned. Multiplying pure numbers together does not
(and cannot) cause units to appear; therefore, raising e to a power (multiplying e by itself
over and over) also results in a pure number without units. Then f0 and g0 must have the
same units as f and g, respectively.
An exponent necessarily has no units. The only way to convert between units is to
multiply by ratios of units and only raising to higher exponents (xa )b = xab yields products
of exponents. Units are algebraic unknowns so that having units in an exponent is equivalent
to having the exponent to be unknown. . . not to know how many times to multiply the base.
We might invent a rule or a convention simply to ignore the units – simply pretend that they
are not there – just raise the base to whatever number is there. But that would mean that
1.6332 = 50.3048 m = 51.000 ft = 5
(A.9)
which is clearly not true. On the other hand, requiring that exponents have no units works
out a little better. To show this we re-arrange our english-metric conversions a little
1 = 3.2808
ft
ft
and
= 0.3048
m
m
(A.10)
and manipulate them similar to the way we did above. Let b be some arbitrary number and
note that
ft
b = b1 = b3.2808 m = b(3.2808)(0.3048) = b1
(A.11)
153
APPENDIX A: Physical Units
which is self-consistent.
Exponents must be pure numbers. For similar reasons the arguments of logarithms must
also be unitless, pure numbers. To see this recall that
x
ln
x0
= ln(x) − ln(x0 )
(A.12)
If x and x0 have the same units, the units cancel on the left and leave a pure number to
be the logarithm’s argument. If they have different units, then any unit conversion applied
to x0 on the right would change the value subtracted from ln(x) thus implying that the
quantity on the left can simultaneously be equal to both values. So, how do we deal with
the right side of Equation (A.12) if x and x0 have units? We understand that we actually
mean something different:
ln(x) − ln(x0 ) = ln(x) − ln(x0 ) + ln(a) − ln(a) = ln(x/a) − ln(x0 /a) = ln
x
x0
(A.13)
The constant a must have the same dimensions as x and x0 , and although it cancels entirely
from the expression, it must be there to make the logarithm’s dimensionless argument make
sense. Incidentally, this is also why logarithmic scales like the Richter scale for earthquakes
and the dB scale for sound always have a reference intensity (a definite value with units),
equivalent to x0 or a in the discussion above.
Sine, cosine, and tangent are trigonometric functions whose arguments are usually derived
from angles. Trigonometric functions arguments are dimensionless, but they are not unitless;
these arguments must have the units of their angular measure. What this means is that if you
scale physical dimensions, the angles do not change. . . if you change your angular measure,
then the angle’s numerical value (degrees or radians) does change. Frequently, we deal with
expressions like
x(t) = x0 cos(ωt + φ)
(A.14)
If x has units of m and t has units of s, what are the units of x0 , ω, and φ? The cosine function
itself has no units so x0 has the units of x. The argument of the cosine is a polynomial, so each
term must have the angular units that the cosine function needs. The natural units of angle
are radians so that a circle has 2π radians. The units of ω must be rad/s. You might notice
a similarity between logarithms, exponentials, and trigonometric functions: their arguments
are all dimensionless. This is not an accident. Mathematics typically concerns functions
applied to numbers. Thus, mathematical expressions tend to be defined in a way such that
they have no dimensions. It is only in physics, where we have to compare real measurements
of different quantities, where the reference units appear. Therefore, in these mathematical
functions, we must convert the argument to pure numbers for the expressions to make sense.
154
Appendix B
Using Vernier Graphical Analysis
Additional guidance is generally provided in the lab experiment chapters.
Helpful Tip
There are two version of this software on the lab computers. The older one, ‘Gax’ is
not well-liked and has caused many TA and student headaches throughout the years.
The newer version, ‘Graphical Analysis 3.4’ (Ga3) is more functional and reliable but
requires a few more steps to get it to do what you need it to do. Please use Graphical
Analysis 3.4 in this course. Excel and Gax are always available if you prefer, however.
When we perform a least squares fit to a mathematical model, we are effectively compiling
all of the knowledge gained by our data into a much smaller set of fitting parameters. To
the extent that our data applies to this particular model, the experimental errors that are
inevitable in measurements are averaged out so that we might utilize the fitting parameters
to improve upon a prediction of our model beyond the data points themselves. This does not
mean that the fitting parameters have no uncertainties associated with them; indeed they
do have and it is essential that we specify each uncertainty when we discuss the parameter.
Many times Graphical Analysis 3.4 does not show the uncertainties in fitting parameters
by default. We can always ask it to do so by right-clicking the parameters box, “Properties...”, and select “Show Uncertainties”. We can also specify other properties in the fitting
parameters such as the number of significant digits.
Not only is the older Gax somewhat unstable, but it also offers meaningful estimates
of fitting parameter uncertainties only for the separate ‘linear regression’; custom models
have no convenient way to get uncertainty estimates. Since fitting parameters are effectively
measurements that the computer has deduced from the data, it is essential that we be able
to specify the uncertainties and the units that must accompany them. These are the reasons
why we prefer Ga3 that has a less obvious user interface.
155
APPENDIX B: Graphical Analysis Software
156
Appendix C
Using Microsoft Excel
C.1
Creating plots and curve fits
Helpful Tip
The primary advantage of Excel is that students have access to it at home. However,
it is more challenging to perform statistical-based fits in Excel unless you write your
own spreadsheet or macros. It is recommended that you perform your data analysis
with Graphical Analysis 3.4 in the lab. However, you always have access to Excel in
many locations in case you want to plot outside the lab.
This short list of resources will help guide you in creating figures in Excel, if you decide
to use it.
• A good introduction to basic graphing in Excel is provided by the LabWrite project:
https://www.ncsu.edu/labwrite/res/gt/graphtut-home.html
• Curve fitting in Excel can be performed, but sometimes it is much more painful than
using a dedicated data analysis program. For least-squares curve fitting, this link
details how to use Excel:
http://www.jkp-ads.com/articles/leastsquares.asp
Neither do Excel’s least-squares fitting parameters come specified with uncertainty
estimates even after you go through these acrobatics.
• We can use Excel’s “LINEST” function to provide complete statistics on straight lines.
See ‘linest’ in Excel’s Help files to learn more about its usage.
157
APPENDIX C: Using Excel
C.2
Performing Calculations
All calculations in spreadsheets begin with “=”. First, select the cell that will hold the result
of the calculation, type “=”, and enter the formula to be evaluated. Typing “=5+9” and
‘Enter’ will yield “14” in the cell; the cell beneath will then be selected. If you need a cell to
contain ‘=’ instead the results of a calculation, precede it with a single quote ‘0’. . . anything
you type after that will be displayed verbatim. Even numeric characters won’t be numbers
after ‘0’.
If this was the extent of their capabilities, spreadsheets would not be very popular. Each
spreadsheet cell is at the intersection of a column having alphabetic label at the top and a
row having numeric label at the left. ‘A1’ is the cell at the top left corner of the sheet, ‘C8’
is at the eighth row and third column, and ‘Z26’ is at the 26th row and the 26th column.
After column ‘Z’ comes column ‘AA’ to ‘AZ’, ‘BA’ to ‘BZ’,. . . , ‘ZA’ to ‘ZZ’. If even more
columns are needed, three, four, and five characters can be used. Column ‘numbers’ count
up just like decimal digits, but column designations have base 26 instead of base 10.
As an exercise we could put the numbers 1-10 in cells A1:A10. Then in, say, B7 we could
type ‘=A1+A2+A3+A4+A5+A6+A7+A8+A9+A10’ to add the numbers (55). After we
type ‘=’, we could click on cell A1 to get the computer to place the ‘A1’ in the formula.
This comes in handy in a large project when you don’t remember the cell designation and
it is not visible on the screen.
This is pretty nice and the total (cell B7) will automatically update anytime one or more
of the numbers in A1:A10 changes. However, this would mean a lot of typing if the sum of,
say, A1:A1000 were needed instead. It turns out that spreadsheets have a ‘sum’ function for
adding the contents of cells. “=sum(A1:A10)” would also add the contents of these cells.
ANY block of cells can be specified using “range” designators. “=sum(a1:z6)” will add the
first six rows of the first 26 columns. The function names and column designators are not
sensitive to case. The cell into which the result is to be placed MUST NOT be part of the
range or an error will result. The ‘A1:A10’ or ‘A1:Z6’ can be generated by the computer by
dragging the mouse across the desired range of cells.
In addition to ‘sum’, we could ‘average’, ‘stdev’, ‘count’, etc. to perform statistics on a
range. Many other functions are part of the standard spreadsheet application. A partitioned
list and usage instructions can be generated using the ‘function’ toolbar button; usually the
icon has ‘f ’, ‘fx ’, ‘f (x)’, or such.
Frequently, we want to generate graphs. To do this we first need to generate the
independent (x-axis) values. Enter ‘10’ into say C3 and ‘=0.1+C3’ into C4. Now, go back
to C4 and ctrl+c to copy this formula. Next, drag the mouse from C5 to C103 to select this
range (the cells turn black) and ctrl+v to paste the formula into all of the selected cells.
Now, C3=10, C4=10.1,. . . , C103=20. Click on one of these cells and look at the formula in
the formula bar. The computer has automatically replaced the ‘3’ in ‘C3’ with the correct
number to add 0.1 to the cell above this one! This always happens by default when you copy
and paste the formulas from one cell to another unless you “Edit/Paste Special. . . ” and
specify the details you want pasted.
158
APPENDIX C: Using Excel
For relatively smooth functions, these 101 values will yield a very nice graph. Smaller
increments can also be generated at need for more quickly changing functions. Uniformly
spaced numbers are needed so often that a shortcut exists. Type 10 into C3 and 10.1 into
C4. Next, drag from C3 to C4 to select both and release the mouse button. The bottom
right corner of the selected cells is a drag handle that can be used to extend the pattern
10.0, 10.1, 10.2,. . . by dragging this handle downward with the left mouse button. Rows of
incrementing numbers can be generated similarly.
Now that we have our abscissa, we need to generate our ordinate. Click on D3 and enter
‘=3*sin(C3)’. Go back to D3 and drag the drag handle at the bottom right downward to
D103. Release the mouse button and note that the result is a sinusoid with amplitude 3. This
is OK! but we can generate families of curves with varying amplitudes, frequencies, or phases
quite easily. Enter ‘2’ into D2, ‘2.2’ into E2,. . . , ‘3’ into I2. Now enter “=D$2*cos($C3)”
into D3. Go back to D3, drag the drag handle across to I3, and release the mouse button.
Now, drag the drag handle down to I103 and note that we have generated six sinusoids
with amplitudes given by row 2. The ‘$’ prevented the ‘2’ in ‘D2’ and the ‘C’ in ‘C3’
from changing. Using ‘$A$1’ or ‘$B$3’ would insert the number in A1 or B3 into all of the
formulas; this would allow you to tweak these two numbers by hand to optimize all of the
curves at once.
Practice generating various abscissas and ordinates so that you can remember these
basics. Also practice plotting the results and pasting the plots into a Word document. You
will want ‘scatter plots’ so that you can choose the (x, y) points.
159
APPENDIX C: Using Excel
160
Appendix D
Using Microsoft Word
Helpful Tip
A nice template containing a report outline and hints for performing many of
the functions science reports, journal publications, and books often employ can be
downloaded from each lab’s website. All word processing programs have similar
capabilities and many can import the template. . . although perhaps not seamlessly.
Hopefully, this will get you started using word processing software.
For your electronic write-ups, you can embed figures directly in the Word files, or you
can upload them separately. If you want to embed in Microsoft Word while preparing your
document, here are some useful sources of assistance.
• To embed an Excel figures directly into Word, you can follow the instructions here:
https://support.office.com/en-us/article/Insert-a-chart-from-an-Excel-spreadsheetinto-Word-0b4d40a5-3544-4dcd-b28f-ba82a9b9f1e1
• If you want to embed a pdf figure into a Word document, you can follow the instructions
here:
https://support.office.com/en-za/article/Add-a-PDF-to-a-document9a293b43-45de-4ad2-a0b7-55a734cf6458
• Another set of instructions for embedding pdfs in Word, with a focus on preserving
quality, can be found here:
https://pagehalffull.wordpress.com/2012/11/20/quick-and-easy-way-to-insert-a-pdfgraph-or-diagram-into-a-microsoft-word-document-without-losing-too-much-quality/
• For embedding more general images in Word, and using word wrapping, see here:
https://support.microsoft.com/en-us/kb/312799
161
APPENDIX D: Using Word
With Microscoft Word, there are usually many ways to accomplish the same task. Some
produce better results than others. This is why you always have the option of uploading
figures and images separately from the text of your write-up.
Helpful Tip
Your goal for writing in this lab is clarity in communication, not professional quality
documents. Beginning students have much difficulty including enough background
information about their experiment and apparatus and they tend to include too much
mundane detail that applies only to their specific apparatus instead. Eventually our
work will be read by scientists all over the world, so it is essential that we practice
including enough information about our apparatus and procedure that everyone in the
world can understand our data while simultaneously avoiding these mundane details
that will tend to confuse readers without our apparatus in front of them.
162
Appendix E
Submitting a Report in Canvas
Preparation
Your lab report should be written in either Microsoft Word or be converted to a text-readable
pdf. Every student at Northwestern has access to Microsoft Word and Excel for lab report
preparation. JPEG format is not allowed for the main text.
Both Word and pdf formats allow your TA to provide helpful feedback using Canvas’
SpeedGrader system. Experience has shown that this online feedback is popular to students
in the 136 labs. This formatting requirement is therefore beneficial to everyone involved.
If possible, it is easiest if all of your files are merged into a single document. In Word,
images and figures can be embedded directly into the text file. If you are submitting a
pdf prepared in another method, it is possible to attach images and figures saved in the
lab as pdf documents into a single pdf file. Adobe Acrobat Professional can accomplish
this. Alternatively, you can merge pdf files online. One possible provider is PDFMerge
(http://www.pdfmerge.com/).
If you cannot put all of your content into a single file, it is accessible to load figures as
separate files (such as jpeg files). If you submit as separate files, you should refer to each
uploaded figure in some other part of your Lab Report. Your TA is not required to view
or grade any document that is not referred to in other graded sections of your report. It is
recommended that you name your files “Figure X” where X is a number. Then you can refer
to each figure by name. Alternatively, you can upload figures as a single document such as
a pdf, and have the appropriate labels on the figures in each document. Remember: a lab
report is practice in communication of ideas and activities. Failure to make references to
uploaded figures clear to your TA can result in lost points.
Submission
To submit your lab report, open the assignment in the Module on Canvas. Click the “Submit
Assignment” link.
163
APPENDIX E: Submitting to Canvas
Under the File Upload tab, select the “Choose File” button and select the appropriate
file. You can press “Add Another File” to create another upload link. When all files are
ready and you agree to the TurnItIn pledge, you can press “Submit Assignment”. You are
able to re-submit your assignment to Canvas, although if it is late it will be flagged. You
should also be able to view your TurnItIn similarity score a few minutes after submission.
Your TA will be able to see all submitted files in the Canvas grading system.
It is probably easiest on your TA if the first file that you upload is your main lab
report text, followed by figure files in order. Do not make life harder for your
TAs as they grade your work!
164