* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download THE NATURE OF ELECTROMAGNETIC WAVES
Speed of gravity wikipedia , lookup
History of optics wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Speed of light wikipedia , lookup
Faster-than-light wikipedia , lookup
Time in physics wikipedia , lookup
Electromagnetism wikipedia , lookup
Refractive index wikipedia , lookup
Circular dichroism wikipedia , lookup
Diffraction wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
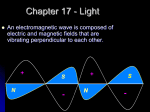
LPH-L2 THE NATURE OF ELECTROMAGNETIC WAVES Light consists of electromagnetic waves moving through space. Figure 4 is a representation of a plane-polarized electromagnetic wave at one instant in time. The concept of polarization is discussed in detail in a later section of this module. Fig. 4 Three-dimensional model of plane-polarized EM waves This wave consists of variations in two types of fields in space. In this case, the electric field (E) always oscillates vertically to form an electric wave; the magnetic field (B) always oscillates horizontally to form a magnetic wave. The two fields are perpendicular to each other, and both are perpendicular to the direction of propagation of the wave. All electromagnetic waves have this same basic composition. They differ only in frequency and wavelength. THE ELECTROMAGNETIC SPECTRUM The span of frequencies and wavelengths covered by electromagnetic radiation is indicated by portion A of Figure 4. Devices that produce or detect electromagnetic waves must be designed to operate at the frequency of the waves they emit or receive. Radio transmitters and receivers operate at frequencies in the 103- and 107 -Hz range and are designed to emit or respond to these frequencies. X-ray tubes and films are designed for use in the 1017- to 10l9-Hz frequency range. Lasers produce coherent light in the frequency and wavelength range indicated by portion B of Figure 4. This range includes the spectral regions commonly identified as the infrared, visible, and ultraviolet regions. The human eye responds to the visible spectrum given in portion C of Figure 5. 1 LPH-L2 Fig. 5 The electromagnetic spectrum The most important ideas summarized in figure 5 are: 1. Electromagnetic waves span over many orders of magnitude in wavelength (or frequency). 2. The frequency of the electromagnetic radiation is inversely proportional to the wavelength. 3. The visible spectrum is a very small part of the electromagnetic spectrum. 4. Photon energy increases as the wavelength decreases. The shorter the wavelength, the more energetic are its photons Table 1 characterizes the spectral regions within which laser emissions and identifies that portion of the eye that is most susceptible to damage by each type of emission. TABLE 1. SPECTRAL REGIONS OF LASER OUTPUTS AND PARTS OF THE EYE MOST SUSCEPTIBLE TO DAMAGE Wavelength (nanometers) Frequency (x 1014 Hz) FAR-MID UV 20–320 150–9.4 Eye part susceptible to damage Cornea NEAR UV 320–390 9.4–7.7 Lens, Cornea Spectral Region 2 LPH-L2 VISIBLE 390–750 7.7–4.0 Retina NEAR IR 750–1400 4.0–2.1 Iris, Retina NEAR-MID IR 1400–3000 2.3–1.0 Cornea, Retina 3000–500,000 1.0–0.006 MID-FAR IR Cornea Examples for elecromagnetic waves are: 1. Radio-waves which have wavelength of the order of meters, so they need big antenas (The dimensions of an antena are of the same order of magnitude as the wave). 2. Microwaves which have wavelength of the order of centimeters. As an example: in a microwave oven, these wavelengths can not be transmitted through the protecting metal grid in the door, while the visible spectrum which have much shorter wavelength allow us to see what is cooking inside the microwave oven through the protecting grid. 3. x-Rays which are used in medicine for taking pictures of the bone structure inside the body. 4. Gamma Rays which are so energetic, that they cause ionization, and are classified as ionizing radiation. INDEX OF REFRACTION All electromagnetic waves travel through a vacuum at the constant speed of c = 3 10נ8 m/sec. When these waves travel through a transmitting material, however, their speed is reduced. The index of refraction of a material is the ratio of the speed of light in a vacuum to its speed in that material and is given by Equation 8. Equation 8 where: n = Index of refraction. V = Speed of light inside material. The frequency of a light wave does not change when it enters a material, but its wavelength is reduced (Figure 6). The index of refraction is also the ratio of wavelength in vacuum to the wavelength in the material (Equation 9). 3 LPH-L2 Equation 9 where: 0 = Wavelength in vacuum. i = Wavelength in material. Fig. 6 Wavelength reduction in material When light leaves a material and enters a vacuum, it returns to speed c and to wavelength 0? The index of refraction of air is about 1.0003, but is assumed to be 1.0 in most applications. Examples D and E illustrate the application of Equations 8 and 9. EXAMPLE D: INDEX OF REFRACTION OF RUBY Given: Light travels through a ruby laser rod at a speed of 1.74 10נ8 m/sec. Find: Index of refraction of ruby. Solution: EXAMPLE E: SPEED AND WAVELENGTH OF LIGHT IN GLASS Given: 4 A HeNe laser beam ( = 633 nm) travels through a glass window with an index of LPH-L2 refraction of 1.65. Find: Speed and wavelength inside the glass. Solution: We saw that the velocity of light in matter is slower than in vacuum. This slower velocity is associated with reduced wavelength: = 0/n , while the frequency remains the same (see figure 7). Figure 7 Change of wavelength in matter Example The velocity of Red light (= 0.6[m]) in a certain medium is 1.5*108 [m/s]. What is the wavelength of this light in this material? Solution to example 1.1: First find the index of refraction: Using n, calculate the wavelength in the material: Conclusion: The wavelength of Red light in a material with an index of refraction of 2.0, is 0.3 [m] 5 LPH-L2 H.W Wavelength Color Frequency (Hz) Angstrom M Violet Blue Green Yellow Red 1. The indices of refraction of several materials situated in air are given below. Calculate the velocity of light in each . a. Fused quartz at 643 nm: n = 1.457. b. Zinc crown glass at 434 nm: n = 1.528. c. Fused quartz at 397 nm: n = 1.471. 2-The wavelengths given in Problem 1 are in vacuum. Calculate the wave lengths inside the materials. 3-Calculate the wavelengths of the following frequencies of light. 1. a. 1.34 10נ14 Hz. b. 260.8 THz. c. 5.83 10נl4 Nz. 4-Calculate the periods of the waves in Problem3 6 LPH-L2 7