* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download chapter (ii) characteristics of fluids
Computational fluid dynamics wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Airy wave theory wikipedia , lookup
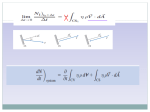
Coandă effect wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Fluid thread breakup wikipedia , lookup
Force on Floating bodies: 1: Archimedes' Principle: Archimedes' principle states that “the buoyant force has a magnitude equal to the weight of the fluid displaced by the body and is directed vertically upward”. To illustrate Archimedes' principle mathematically consider a body of arbitrary shape, having a volume V , that is immersed in a fluid as shown in Fig. (a). We enclose the body in a parallelepiped and draw a free-body diagram of the parallelepiped after removing the body as shown in Fig. (b). 1 The force the body is exerting on the fluid, FB will be: (2.12) Since: where A is the horizontal area of the upper (or lower) surface of the parallelepiped, and Eq. 2.12 can be written as: i.e; (2.13) where is the specific weight of the fluid and V is the volume of the body. The direction of the buoyant force (which is the force of the fluid on the body), is opposite to that shown in Fig .(b). Therefore, the buoyant force has a magnitude equal to the weight of the fluid displaced by the body and is directed vertically upward. This result is commonly referred to as Archimedes' principle. The buoyant force passes through the centroid of the displaced volume which is called the center of buoyancy. 2 Example A spherical buoy has a diameter of 1.5 m, weighs 8.50 kN, and is anchored to the seafloor with a cable as is shown in Fig. Although the buoy normally floats on the surface, at certain times the water depth increases so that the buoy is completely immersed as illustrated. For this condition what is the tension of the cable? [ seawater 10.1kN / m 3 ]. Solution: The free-body diagram shows that: Since, and FB 3 2: Stability of Floating body: Stability or instability will be determine by whether a righting or overturning moment is developed when the centre of gravity and centre of buoyancy move out of vertical alignment. Any inclination for a floating body should result in turning moment. This moment created due to the movement of the centre of buoyancy from c to c`, and since the buoyancy force and the body weight are equal in magnitude and opposite in direction they will form a couple. If that couple tends to move the body back to its original vertical position, as shown in figure (a), the floating body will be stable and the couple in this case will be Righting Couple or Restoring Couple. Stability of a floating body stable configuration. (a) 4 Otherwise, the floating body will be unstable and the couple in this case will be Overturning Couple, as shown in Figure (b). Stability of a floating body unstable configuration. (b) 5 M C` C The vertical line through c` intersects the original centre line at point “M” ,this point is called “Meta Centre”. And the distance “MG” is called the “Meta Centric Height”, which is the direct measure of stability. When “M” is above “G” the floating body is stable. When “M” is below “G” the floating body is unstable. When “M” is on “G” the floating body is in neutral equilibrium. The distance “MC” can be obtained from the formula: CM I Vimmersed Where, I is the moment of inertia of the area of intersection between the plane surface of liquid and the body on its vertical position around the axis of rotation. 6 Pressure Variation in a Fluid with Rigid-Body Motion: The general equation of motion (Eq. 2.2): i.e; (2.14) 2.8.1: Linear Motion: Consider an open container of a liquid that is translating along a straight path with a constant acceleration “a” as shown. Since ax = 0 , it follows from the first of Eqs. 2.14 that, ( 0). In the y and z directions: and 7 Since, p = p(y,z), then: Or, Line of constant pressure, where dp = 0, therefore, the slope of this line is: (2.15) Since at the free surface the pressure is constant, so, all lines of constant pressure will be parallel to the free surface. For the special case in which ay = 0, az ≠ 0, which corresponds to the mass of fluid accelerating in the vertical direction, Eq.2.15 indicates that the fluid surface will be horizontal. However, the pressure distribution is not hydrostatic, but is given by the equation: (2.16) 8 15cm 25cm 25cm Example : The cross section for the fuel tank of an experimental vehicle is shown in Fig. The rectangular tank is vented to the atmosphere, and a pressure transducer is located in its side as illustrated. During testing of the vehicle, the tank is subjected to a constant linear acceleration, ay. (a) Determine an expression that relates ay and the pressure (in kN/m²) at the transducer for a fuel with a SG = 0.65. (b) What is the maximum acceleration that can occur before the fuel level drops below the transducer? 9 Solution: The slope of the fuel surface, according to Eq.2-15 for az = 0, can be expressed as: Thus, 0.25m or 0.25m Since there is no acceleration in the vertical, z- direction, the pressure along the wall varies hydrostatically. Thus, the pressure at the transducer is: Where h is the depth of fuel above the transducer, and therefore: p (0.65)(1000)(9.807)[0.15m z1 ] ay (0.65)(1000)(9.807)[0.15m 0.25m ] g a 956.18 1593.64 0.96 1.59 ay g y g ( N / m2 ) ( kN / m 2 ) 10 (b) The limiting value for (ay)max (when the fuel level reaches the transducer) can be found as: 0.25m 0.15m 0.25m 3 5 = 0.6 g Remember That: Even though a fluid may be in motion, if it moves as a rigid body there will be no shearing stresses present. 11 2: Rigid-Body Rotation: A fluid contained in a tank that is rotating with a constant angular velocity about an axis will rotate as a rigid body. Since the paths of the fluid particles are circular, it is convenient to use cylindrical polar coordinates r,Ѳ, and z. Then the pressure gradient can be expressed as: (2.17) 12 It is known from elementary particle dynamics that the acceleration of a fluid particle located at a distance r from the axis of rotation is equal in magnitude to rω², and the direction of the acceleration is toward the axis of rotation as is shown in the figure. Thus: and from F,q.2.2: Since, p = p(r,z), then: Or, (2-18) surface of constant pressure, where dp = 0, therefore: → (2-19) 13 This equation reveals that these surfaces of constant pressure are parabolic as shown in Fig. Integration of Eq. 2.18 yields: Then: (2-20) 14 Relationship Between the Change in Fluid Level and the Angular Velocity: As shown in Fig. and from Eq. 2.19, it follows that: The initial volume of fluid in the tank, V i is equal to: 15 The volume of the fluid with the rotating tank can be found with the aid of the differential element shown in Fig. Then the volume is: Since the volume of the fluid in the tank must remain constant (assuming that none spills over the top), it follows that: Or, (2-21) Which is the relationship we were looking for. 16