Download 2.4: The Chain Rule

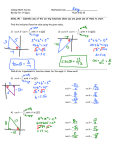
AP CALCULUS
Section Number:
LECTURE NOTES
MR. RECORD
Day: 15
Topics: The Chain Rule
2.4 A
1. The Chain Rule
Perhaps the best way to introduce this new differentiating technique is to show you the types of functions
that would require its use. The table below illustrates pairs of similar functions that can be differentiated
with and without the Chain Rule.
Without the Chain Rule
With the Chain Rule
y  x2  1
y  x2  1
y  sin x
y  sin 6 x
y  3x  2
y   3x  2 
5
y  x  tan  x 2 
y  x  tan x
The Chain Rule
If y  f (u ) is a differentiable function of u and u  g ( x ) is a differentiable function o f x , then
y  f ( g ( x )) is a differentiable function of x and
dy dy du


dx du dx
or equivalently
d
 f ( g ( x))  f   g ( x)   g ( x).
dx
Example 1: Decompositions of a Composite Function.
Complete the table.
y  f ( g ( x ))
u  g ( x)
1
x 1
a.
y
b.
y  sin 2 x
c.
y  3x 2  x  1
d.
y  tan 2 x
y  f (u )
Example 2: Find
dy
for y  ( x 2  1)3
dx
The General Power Rule (“Chain Rule Short-Cut”)
If y   u ( x) , where u is a differentiable function of x and n is a rational number, then
dy
n 1 du
 n  u ( x) 
dx
dx
or equivalently
n
d n
u   nu n 1  u.
dx  
Example 3: Find
a. y  (3x  2 x 2 )3
b. y  3 ( x 2  1)2
c. y 
7
(2 x  3)2
dy
for each of the following.
dx
AP CALCULUS
Section Number:
LECTURE NOTES
Topics: The Chain Rule
- Differentiating tan(x), cot(x) sec(x) and csc(x)
- Nested Chain Rules
2.4 B
2. Derivatives of The Other Trigonometric Functions
Recall from Section 2.2,
d
d
 sin x   cos x
 cos x    sin x
dx
dx
Now, we will take a look at the derivatives of the other four trigonometric functions.
Derivatives of Trigonometric Functions
d
 tan x   sec2 x
dx
d
 sec x   sec x tan x
dx
Example 4:
Prove
d
 cot x    csc2 x
dx
d
 csc x    csc x cot x
dx
d
 tan x   sec2 x
dx
Example 5: Find the derivative of each of the following.
a. y  x  tan x
Example 6: Differentiate both forms of y 
b. y  x sec x
1  cos x
 csc x  cot x
sin x
MR. RECORD
Day: 16
3. Trigonometric Functions and the Chain Rule
The “Chain Rule versions” of the derivatives of the six trigonometric functions are as follows
d
d
 sin u    cos u   u
 cos u     sin u   u
dx
dx
d
d
 tan u    sec2 u   u
 cot u     csc2 u   u
dx
dx
d
d
 sec u    sec u tan u   u
 csc u     csc u cot u   u
dx
dx
Example 7: Find the derivative of each trigonometric function.
a. y  sin 2 x
b. y  cos(3x  1)
c. y  sec 4 x
4. Trigonometric Functions That Require Repeated Use of the Chain Rule
Example 8: Find the derivative of each trigonometric function.
a. y  sin 4 3x
2  3x 
c. y  cot 3  
 2 
 x
b. y  sec  
 2
5. Nested Product/Quotient and Chain Rules
Lastly, we will see how the Chain Rule can be used in conjunction with the Product and Quotient Rules.
It takes a bit more planning and organization to take the derivative correctly, but it’s really not too bad.
Furthermore, there is a special technique used to simplify these answers.
Example 9: Differentiate and simplify f ( x)  x 2 1  x 2 .
Example 10: Differentiate and simplify f ( x) 
x
3
x 4
2
.
 3x  1 
Example 11: Differentiate and simplify f ( x)   2
 .
 x 3
2