Download Figure 7.1, 7.2

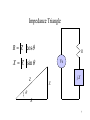
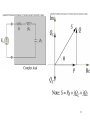
Chapter 7: AC Power
Current and voltage waveforms for
illustration of AC power
Figure 7.1,
7.2
1
Instantaneous and Average Power
p(t )  v(t )i (t )  VI cos(t ) cos(t   )
VI
VI
P(t ) 
cos( )  cos(2t   )
2
2
1T
1 T VI
1 T VI
Pav   p(t )dt   cos( )dt   cos(2t   )dt
T0
T0 2
T0 2
VI
1 V2

cos( ) 
cos (Average Power)
2
2 Z
2
Instantaneous Power Calculations
p  vi in watts
vt   Vm cos(t   v )
p
it   I m cos(t   i )
Vm I m
V I
V I
cos( v   i )  m m cos( v   i ) cos 2t  m m sin(  v   i ) sin 2t
2
2
2
 v is the voltage phase angle
 i is the curent phase angle
3
Instantaneous and average power dissipation corresponding to the
signals plotted in Figure 7.2
Figure 7.3
4
Instantaneous Power
magnitude
power
voltage
wt
current
Instantaneous power has twice the frequency of the voltage or current
5
RMS Value
•
It is customary in AC power analysis to employ the RMS value of the AC voltage
and currents in the circuit (Read Section 4.2).
Vrms 
V
2
I
I rms 
Pav 
~
V
~
I
2
~
2
V
Z
~ ~
cos  V I cos
6
Impedance Triangle
R  Z cos
R
X  Z sin 
Z
Vs
jX
X

R
7
Power Factor
• The phase angle of the load impedance plays a very
important role in the absorption of power by a load
impedance.
• The average power dissipated by an AC load is dependent
on the cosine of the angle of the impedance.
• The term cos () is referred as the power factor (pf).
• The power factor is equal to 0 for purely inductive or
capacitive load.
• The power factor is equal to 1 for a purely resistive load.
8
Complex Power
Apparent Power S
Q

Reactive Power
Pav
Real Power
~ ~
S  Pav2  Q 2  V I
~ ~
Pav  V I cos
~ ~
Q  V I sin 
9
Table
7.2
10
Figure 7.16,
7.17
11
Power factor correction
Figure
7.18,
7.19,
7.20
12