Download Systems of Equations

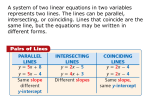
Do Now - Review
Find the solution to the system of equations:
x–y=3
x+y=5
Systems of Equations - Definitions
Systems of Equations – two or more equations together
that offer a solution to a problem.
On the graph, the solution to a system of linear equations
is the point where the lines intersect.
If when we graph the equations we see:
Intersecting Lines – there is one solution to the system.
Same Line – there are an infinite number of solutions.
Parallel Lines – there is no solution to the system.
Intersecting Lines
• The point where the lines
intersect is your solution.
• The solution of this graph is
(1, 2)
(1,2)
Coinciding Lines
• These lines are the same!
• Since the lines are on top of
each other, there are
INFINITELY MANY
SOLUTIONS!
• Coinciding lines have the
same slope and
y-intercepts.
2
Slope =
=2
1
y-intercept = -1
Parallel Lines
• These lines never intersect!
• Since the lines never cross,
there is
NO SOLUTION!
• Parallel lines have the same
slope with different yintercepts.
2
Slope =
=2
1
y-intercept = 2
y-intercept = -1
Solving a System of Equations by Graphing
There are 3 steps to solving a system using a
graph.
Step 1: Graph both equations.
Graph using slope and y – intercept.
Solve each equation for y first if
necessary.
Step 2: Do the graphs intersect?
This is the solution! (No or infinite
solutions are possible.)
Step 3: Check your solution.
Substitute the x and y values into
both equations to verify the point is a
solution to both equations.
Back To The Do Now
x–y=3
x+y=5
Systems of Equations Ex. 1
6
Y = -x + 5
-10
and y = x - 3
4
2
-5
5
-2
Solution (4,1)
-4
-6
Ex. 2
y = -x + 5
and
2x + 2y = -8
6
4
2
-10
-5
5
-2
-4
-6
3. What is the solution of this system?
3x – y = 8
2y = 6x -16
1.
2.
3.
4.
(3, 1)
(4, 4)
No solution
Infinitely many solutions
Ex. 4
x = 2 and 2x + y = 1
6
4
2
-10
-5
5
-2
-4
-6
7-1 Graphing Systems of Equations
Using our Calculators
Solve the system: y = -2x + 9 and y = 3x - 4
1.
2.
Enter the first equation into Y1.
Enter the second equation into Y2.
3. Hit GRAPH.
4. Use the INTERSECT option to find where the
two graphs intersect (the answer).
2nd TRACE (CALC) #5 intersect
Move spider close to the intersection.
Hit ENTER 3 times.
5. Answer: x = 2.6 and y = 3.8